中小学数学12

题目：设AB是圆的直径，过A，B分别作弦AC，BD相交于点E，证明：AE·AC+BE·BD＝                     分析：这类题通常与相似三角形相关，式子中出

题目：

设AB是圆的直径，过A，B分别作弦AC，BD相交于点E，证明：AE·AC+BE·BD＝

分析：这类题通常与相似三角形相关，式子中出现的AE，BE提示我们过点E作EF⊥AB于F而构造相似三角形，如图。

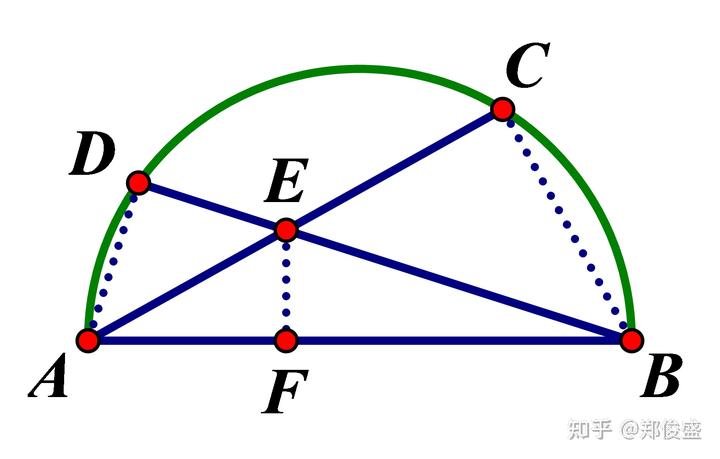
如此一来，因为∠ACB＝90°，∠AFE＝90°，∠BAC＝∠BAC；∠BDA＝90°，∠BFE＝90°，∠ABD＝∠ABD，所以

ΔACB∽ΔAFE，ΔBDA∽ΔBFE

所以

AB：AE＝AC：AF；AB：BE＝BD：BF

即

AE·AC＝AB·AF；BE·BD＝AB·BF

两式相加，得

AE·AC+ BE·BD＝AB·AF+AB·BF＝AB(AF+BF)=AB·AB=