ANNOY & HNSW
ANNOY我们之前已经介绍了IVF的ANN检索算法,核心思路就是对全局的向量做聚类,然后在搜索的过程中只对特定的聚类簇中包含的特征向量
ANNOY
我们之前已经介绍了IVF的ANN检索算法,核心思路就是对全局的向量做聚类,然后在搜索的过程中只对特定的聚类簇中包含的特征向量做检索,ANNOY,全名Approximate Nearest Neighbors Oh Yeah,也是使用类似的思路,不过和IVF相比,采用类似二叉树的方式进行检索,整个算法表达上更加朴素清晰,具体可以参考以下这篇链接,实在是笔者看到过的对ANNOY解释的最为清晰的一篇文章,笔者在此仅做以上介绍和对比,就不造重复的轮子了。
Annoy搜索算法(Approximate Nearest Neighbors Oh Yeah)SW
HNSW(Hierarchical Navigable Small Worlds)是一种基于图的ANN搜索算法,谈到HNSW,我们就不得不从从SW说起,一种通俗的分类方式,将图分为三种:
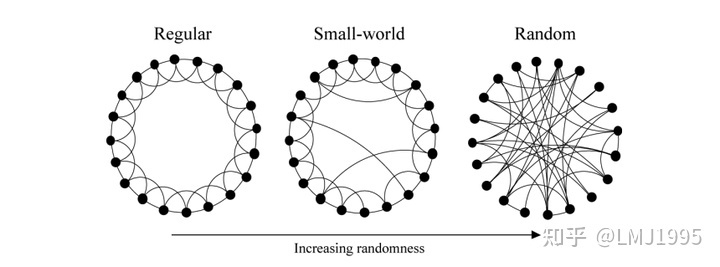
- 正则图(Regular Graph):指各顶点的度均相同的无向简单图
- 随机图(Random Graph):指各顶点随机进行连接的无向简单图
- 小世界(Small World)
这里我们先忽略小世界的定义,关注正则图与随机图之间的区别,我们使用以下代码来模拟正则图和随机图
# Consider the scenario of 99 verticesnnum_vertex = 99nn# predefined reg_degree as 4nreg_degree = 4nn# generate a regular graphndef Gen_Reg_Graph(num_vertex, reg_degree):n tmp_dict_reg = {}n inf_big = 999nn for i in range(num_vertex):n tmp = []n for j in range(reg_degree // 2):n tmp.append((i + j + 1)% num_vertex)n tmp.append((i - j - 1)% num_vertex)n tmp_dict_reg[i] = tmpn n reg_graph = np.ones((num_vertex, num_vertex)) * inf_bign for i in range(num_vertex):n for j in tmp_dict_reg[i]:n reg_graph[i][j] = 1n # keep diaganol as 0n reg_graph[i][i] = 0n return reg_graphnnreg_graph = Gen_Reg_Graph(num_vertex, reg_degree)nprint(reg_graph)nn# generate a random graphndef Gen_Rnd_Graph(num_vertex):n tmp_dict_reg = {}n inf_big = 999n rnd_graph = np.ones((num_vertex, num_vertex)) * inf_bign # randomly set two vertices connectedn for i in range(num_vertex):n for j in range(num_vertex):n if random.randint(1,20) % 17 == 0:n rnd_graph[i][j] = 1n rnd_graph[j][i] = 1n # keep diaganol as 0n rnd_graph[i][i] = 0n return rnd_graphnnrnd_graph = Gen_Rnd_Graph(num_vertex)nprint(rnd_graph)nn# Dijkstrandef dijkstra(start, graph):n passed = [start]n nopass = [x for x in range(graph.shape[0]) if x != start]n dis = graph[start]n n while len(nopass):n idx = nopass[0]n for i in nopass:n if dis[i] < dis[idx]: idx = inn nopass.remove(idx)n passed.append(idx)nn for i in nopass:n if dis[idx] + graph[idx][i] < dis[i]: dis[i] = dis[idx] + graph[idx][i]n return disnndis_reg = dijkstra(0, reg_graph)nprint("Distance in regular graph {}".format(dis_reg))ndis_rnd = dijkstra(0, rnd_graph)nprint("Distance in random graph {}".format(dis_rnd))
我们首先通过以上代码生成了一个正则图和一个随机图,并通过dijkstra(随手扒了一个dijktra的python实现)来观察其中一个点到其他点的距离,最终得到以下输出(这里的distance值可以理解为从一个顶点到另一个顶点的“跳跃次数”)
Distance in regular graph [ 0. 1. 1. 2. 2. 3. 3. 4. 4. 5. 5. 6. 6. 7. 7.n 8. 8. 9. 9. 10. 10. 11. 11. 12. 12. 13. 13. 14. 14. 15.n 15. 16. 16. 17. 17. 18. 18. 19. 19. 20. 20. 21. 21. 22. 22.n 23. 23. 24. 24. 25. 25. 24. 24. 23. 23. 22. 22. 21. 21. 20.n 20. 19. 19. 18. 18. 17. 17. 16. 16. 15. 15. 14. 14. 13. 13.n 12. 12. 11. 11. 10. 10. 9. 9. 8. 8. 7. 7. 6. 6. 5.n 5. 4. 4. 3. 3. 2. 2. 1. 1.]nDistance in random graph [ 0. 3. 1. 2. 3. 2. 2. 3. 3. 2. 1. 1. 2. 1. 1. 2. 3. 3.n 3. 3. 2. 2. 3. 3. 1. 2. 2. 2. 2. 2. 3. 2. 2. 2. 2. 1.n 2. 2. 2. 2. 2. 3. 2. 2. 3. 2. 3. 1. 2. 2. 3. 2. 2. 2.n 3. 3. 3. 2. 2. 2. 2. 2. 3. 2. 2. 2. 3. 2. 2. 3. 2. 2.n 3. 3. 2. 3. 2. 2. 2. 3. 2. 3. 2. 3. 2. 2. 2. 2. 2. 3.n 1. 2. 3. 3. 3. 2. 3. 3. 3.]
不难看出,在正则图中,从一个点到另一个点的搜索次数在特定情况下要远远高于随机图(当然这和我们在随机图中设计的连通的概率也有关系),通常情况下,正则图中的顶点的路径更长,但是同时更聚合,也就是空间中距离相近的两个点是互相连接的。而随机图中的顶点尽管路径更短,但是几乎是完全不聚合的,也就是很难保证在空间中相邻的两个点在图中是相连接的,故而很难在实际的向量检索、ANN等场景中使用随机图。
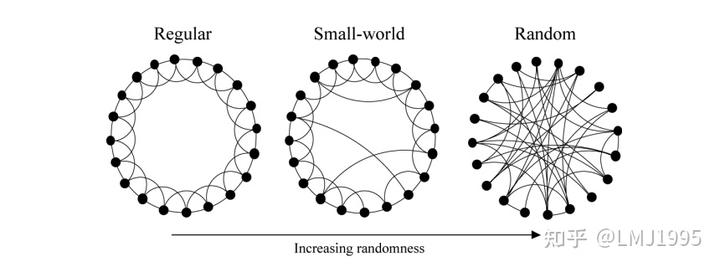
而Small World则基于两者之间,在原本的正则图中类似“击鼓传花”的这个搜索的过程中,偶然的可以在两个相去甚远的点中来个“长传”,这可以极大的加速了整个检索的步骤。
# predefined reg_degree as 4nreg_degree = 4nndef Gen_Reg_Graph(num_vertex, reg_degree):n tmp_dict_reg = {}n inf_big = 999nn for i in range(num_vertex):n tmp = []n for j in range(reg_degree // 2):n tmp.append((i + j + 1)% num_vertex)n tmp.append((i - j - 1)% num_vertex)n tmp_dict_reg[i] = tmpn n sw_graph = np.ones((num_vertex, num_vertex)) * inf_bign for i in range(num_vertex):n for j in tmp_dict_reg[i]:n sw_graph[i][j] = 1n # keep diaganol as 0n sw_graph[i][i] = 0n n # randomly set 2 express wayn for i in range(2):n x = random.randint(0,99)n y = random.randint(0,99)n sw_graph[x][y] = 1n sw_graph[y][x] = 1n return sw_graphnnsw_graph = Gen_Reg_Graph(num_vertex, reg_degree)nprint(sw_graph)ndis_sw = dijkstra(0, sw_graph)nprint("Distance in random graph {}".format(dis_sw))
输出为
Distance in small world graph [ 0. 1. 1. 2. 2. 3. 3. 4. 4. 5. 5. 6. 6. 7. 7.n 8. 8. 9. 9. 10. 10. 11. 11. 12. 12. 13. 13. 14. 14. 15.n 15. 16. 16. 17. 17. 16. 16. 15. 15. 14. 14. 13. 14. 14. 15.n 15. 16. 16. 17. 16. 16. 15. 15. 14. 14. 13. 13. 12. 12. 11.n 11. 10. 10. 9. 10. 10. 11. 11. 12. 12. 13. 13. 14. 13. 13.n 12. 12. 11. 11. 10. 10. 9. 9. 8. 8. 7. 7. 6. 6. 5.n 5. 4. 4. 3. 3. 2. 2. 1. 1.]
NSW
我们回到上面正则图的概念,根据给定的顶点(在实际的检索场景中,常常表现为多个特征向量),我们总是可以通过德劳内三角形的分割方式,将不同的顶点进行联通,然后在图中随机创建Expressway mechanism(上面说的“长传”的学名),也就是建立比较遥远的两个点间的连接。但是这种方法在实际场景中是行不通的,德劳内三角形分割的时间复杂度为 
而论文中解决这个问题的方式却实打实的简单到令人发指,整个NSW图构建的算法步骤可以用伪代码描述如下
V: set of verticesnG: inital state of NSW graphnnfor v_i in V:n V.pop(v_i) # 这一步建议随机在V中选择v_i特征向量n for v_j in G.find_topk_NN(v_i):n G.connect(v_i, v_j)
对,随机选择V中的一个顶点,找到已建立的NSW图中的topk最近邻(NN),将其连接,重复这个过程直到V中的所有的点都已经被便利。
为什么按照上面这个过程就可以得到一个很好的NSW图呢?回想下上面提到的SW具有两个特征,SW具有正则图中的局部聚合的特性,但是同时也有随机图中的Expressway mechanism,而我们随机添加顶点的过程中,在算法的早期,因为图中的点数量较少,所以很容易建立两个遥远的点之间的Expressway,而在算法的后期,因为图中的点数量已经多起来,对于全局的数据空间具有一定的代表性,那么添加的新的点在选取topk的时候,基本上都会选择到其具备相邻的点,那么就保证了SW图中的局部聚合的特性。
跳表
想要更好的理解HNSW,就首先需要理解跳表的原理,跳表是可以理解为一种特殊的链表(下图from百度百科)
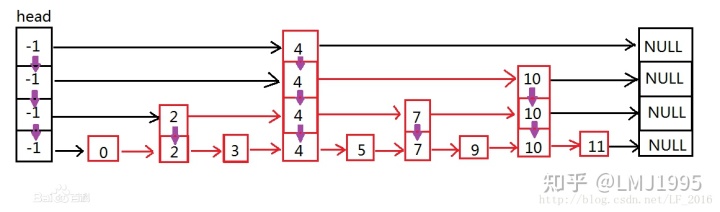
可以看到,跳表其实也使用了我们上文中所说的这种Express Mechanism机制,只不过跳表上的Express Mechanism建立在一维空间之中(类似于数轴),同时由多层链表进一步加速链表上特定元素的搜索过程。
对于一个元素的检索过程,比如检索数字3,首先在顶层的链表中执行比对,在第一层中发现3比head要大,但是比4要小,那么我们就向下进入第二层链表中检索,以此类推。
HNSW
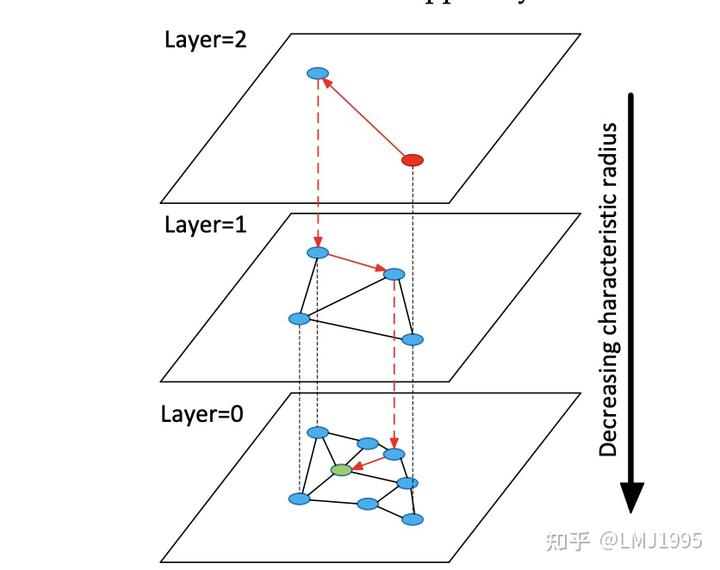
而HNSW就是在普通的NSW之上,结合跳表的思路来进一步优化检索的性能(在高层中进行搜索比在底部局部执行搜索的速度要快得多得多)
我们在检索的过程中,分为两个不同的阶段,分别是建立HNSW图以及在HNSW图中进行检索
建立HNSW图:INSERT
HNSW图的建立可以粗略的被伪代码描述如下(详细描述请移步论文)
vi: vectex to be insertednep: enter point at first layernhighest_layer: fewest verticesnlowest_layer: all verticesnn# specify a layer to insert vininserted_layer = random_ln_gen(vi)nn# go down to the layer vi is inserted, without building new connections (search process)nfor layer in [highest_layaer:inserted_layer]:n NN = Search_Layer(ep, layer, vi)n ep = Select_New_Ep_From_NN(vi, NN)nn# going down to layer0, building new connections at each layernfor layer in [inserted_layer:lowest_layer]:n NN = Search_Layer(ep, layer, vi)n NiceNN = Select_Neighbors(NN) #对于理解HNSW的过程而言,事实上不需要理解Select_Neighbors也可以n Update_Connections(NiceNN, vi)
执行HNSW中的检索:SEARCH
执行HNSW中的检索可以粗略的被伪代码描述如下(详细描述请移步论文)
vi: vertex to be searchednep: enter point at first layernn# go down to the layer vi is inserted, without building new connectionsnfor layer in [highest_layaer:lowest_layer]:n NN = Search_Layer(ep, layer, vi)n ep = Select_New_Ep_From_NN(vi, NN)nnFinal_Search(NN)
SelectNeighbors: Heuristic or not?
在HNSW的搜索中,一次检索的结果很容易因为entrypoint的选择不同而落入局部的最优解
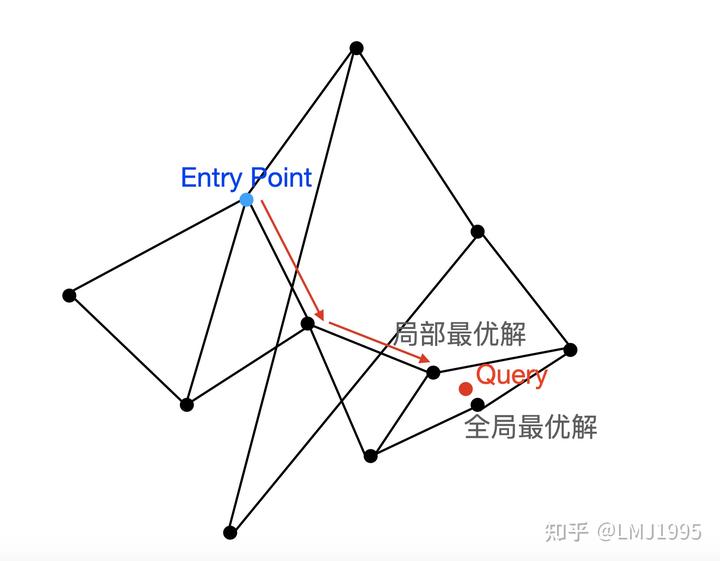
可以看到,在上面的HNSW一次检索(遍历过程)中,在达到了局部最优解后,HNSW的搜索便停止了,而真正的全局最优解则没有被访问到。
为了解决上述问题,我们有两种思路可供选择,一种思路是对于一次检索过程,选择多个可能的EntryPoint,并汇总他们的结果作为最终的结果,另一种思路便是对于一次检索过程,采用启发式的算法(类似深度学习中的老虎机摇臂问题,Exploration vs Exploitation)。
论文中提供了比较考究的两种在Search_Layer得到的NN中进一步选择NN并进行连接的方法,一种是启发式的,一种非启发式的,关于启发式算法的具体实现细节就不在此赘述,如有疑问也欢迎在评论区留言讨论。




