综合能源系统目标函数建立
0. 前言在本章中,我们将对一个实际的综合能源系统(以下简称IES)进行建模,明确该系统优化运行问题的优化变量,并构建起该问题的目标函数
0. 前言
在本章中,我们将对一个实际的综合能源系统(以下简称IES)进行建模,明确该系统优化运行问题的优化变量,并构建起该问题的目标函数。
1. 测试系统介绍
该测试系统为6 bus 电力系统+6 node 热力系统,拓扑如下图所示。其中,三台发电机 G 分别位于 bus 1,4,6,燃气锅炉 GB 位于 node 1,一台热电联产机组 CHP 能够同时向 bus 6 供电和向 node 1 供热,电力负荷同时存在于 bus 1 - bus 6,热力负荷存在于 node 4 - node 6。电能和热能分别沿电网和热力管网从源侧传输至负荷侧。
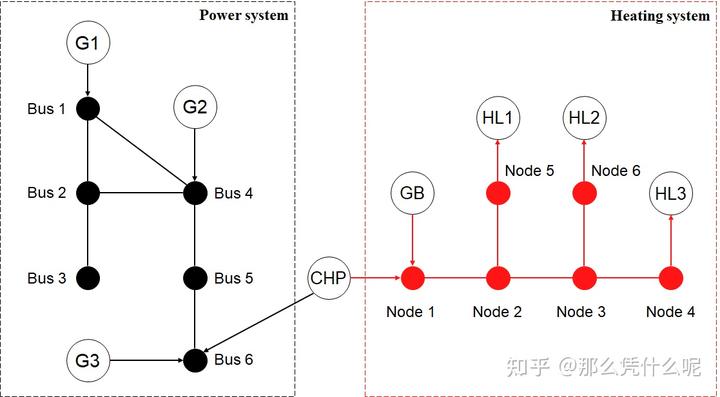
对于该测试系统而言,其优化运行问题可以描述为:在满足末端电力负荷和热力负荷的前提下,最小化系统的运行成本,即让三台发电机、一台燃气锅炉和热电联产机组的总运行成本最小。在建立目标函数之前,首先需要对该系统进行建模,明确优化变量和设备模型。
2. 设备模型
2.1 发电机
发电机产生电能向末端供应电能,其发电成本通常表示为其发电量的二次函数,如下式所示:

式中, 

2.2 燃气锅炉
燃气锅炉通过消耗天然气产生热能(热水)向末端供应热能,其发热成本如下式所示:

式中, 


2.3 热电联产机组
通过消耗天然气,热电联产机组能够同时向末端供应电能和热能,本专栏中采用的运行成本计算公式如下式所示:

式中, 


式中, 

2.4 电网和热力管网
事实上,相比于电网和热力管网模型,设备模型都是十分简单易懂的。在实际编程过程中,大多数的bug都源于管网建模出了问题。电网和热力管网的优化建模问题,分别称为最优电力潮流(Optimal Power Flow,OPF)和最优热力潮流(Optimal Thermal Flow,OTF),由于两者较为复杂,其建模将在接下来的两章中详细介绍。
3. 优化变量和目标函数建立
由此,我们可以确定部分优化变量,并完整的建立起目标函数。优化运行问题本质上是最优化各个设备的出力,因此,发电机的发电量、燃气锅炉的发热量以及热电联产机组的发电量(和发热量)为部分待优化的变量,其代码如下(代码中lb和ub的赋值可暂时忽略,这些值分别代表了优化变量的上下限,由设备性能决定):
p_g1 = m.addVar(lb=g_list[0][4], ub=g_list[0][5], name='power output of generator 1')np_g2 = m.addVar(lb=g_list[1][4], ub=g_list[1][5], name='power output of generator 2')np_g3 = m.addVar(lb=g_list[2][4], ub=g_list[2][5], name='power output of generator 3')np_chp = m.addVar(lb=lb_chp, ub=ub_chp, name='power output of CHP')nh_b = m.addVar(lb=b_list[0][2], ub=b_list[0][3], name='heating output of boiler')
在此基础上,我们可以写出问题的目标函数(同样的,看不懂的系数可暂时忽略,它们代表模型中的价格系数、效率参数等):
obj = price_gas * (p_chp / effi_g2p + h_b / b_list[0][1]) + g_list[0][1] * p_g1 * p_g1 + g_list[0][2] * p_g1 + n g_list[1][1] * p_g2 * p_g2 + g_list[1][2] * p_g2 + g_list[2][1] * p_g3 * p_g3 + g_list[2][2] * p_g3
4. 小结
在本章中,我们建立了系统的物理模型,确定了部分优化变量,并建立了目标函数。在下一章中,我们将详细介绍最优电力潮流问题,由此构建该问题的电力部分约束。




