unity实现计算模型的体积
昨天与群员闲聊,偶然得知有计算模型体积的需要,这需求在游戏行业基本上用不到,一般在工业仿真或者3D打印等方面用得较多,据称
昨天与群员闲聊,偶然得知有计算模型体积的需要,这需求在游戏行业基本上用不到,一般在工业仿真或者3D打印等方面用得较多,据称某群员之前用蒙特卡洛模拟实现了,考虑到各平台语法不太一样,我刚好会一点unity3D引擎,因此复盘一个简单的demo来讲解一下该法的原理。
蒙特卡洛法,又称随机模拟法。它利用了统计学中的一个简单的原理:当试验次数足够大,频率就可以近似地等同于概率。该法的一个典型应用就是蒲丰投针试验:
蒲丰投针问题_百度百科该试验通过求解概率,可以用于计算圆周率,具体推导无需深究,其公式为:当平面上画满了间距为 a 的平行直线,向该平面随机抛掷一个长度为 l (l<a) 的针,则多次抛掷后,针与直线的相交概率为:

于是可以反推出π的近似数值。
回到模型体积的问题上,我们假设这样一个场景:在空间中存有一个模型,模型的外部包有一个稍大的球壳,若我们随机在球壳内生成一个点,那么该点要么在模型内,要么在模型外;由于球壳的体积是已知的,那么统计模型内的点的数量,计算它占总点数的比例,乘以球壳的体积,即为近似的模型体积。
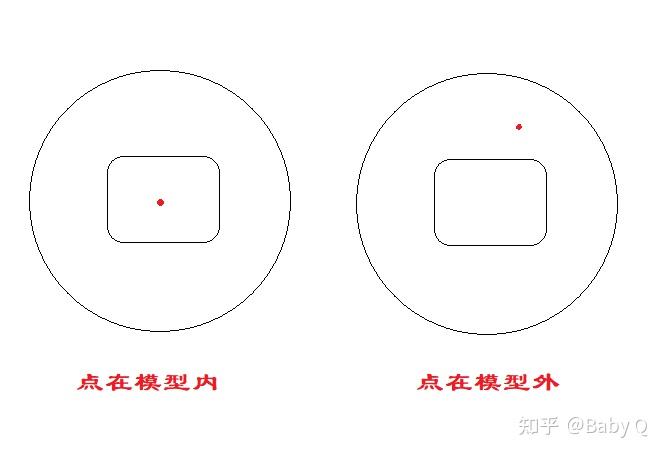
为便于进行测试,我使用6个plane搭建了一个长宽高均为10的立方体(为什么不用自带的cube,这个我们稍后再说),便于后续分析偏差度。
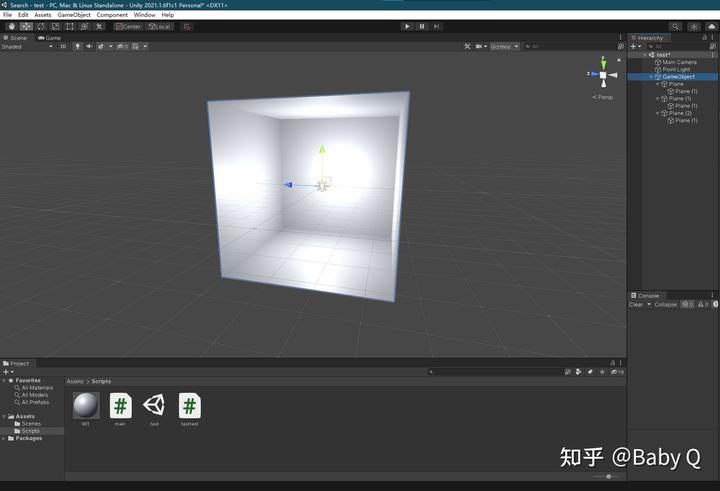
然后动态生成一个半径为25的虚拟球壳,并生成五百万个点进行模拟,以下是具体代码:
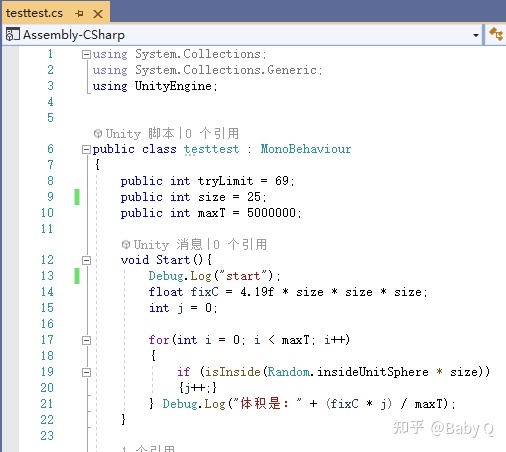
逻辑很简单,for循环五百万次,每次通过random函数生成一个随机的坐标点,并乘以size系数来让它遍布球壳内部,然后进行判定,若在模型内,则对变量 j 累加一次,最后除以总次数计算概率,乘以球壳体积即可,此处的 4.19 是 球形体积公式:V = ⁴⁄₃πr³ 前部的 ⁴⁄₃π 的数值,便于作为固定系数简化运算,以下是多次运行的几次结果:
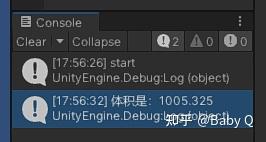
以第一次模拟为例,结果为“体积是1005”,我们搭建模型的标准体积是10*10*10=1000,存有千分之五的误差,还是可以接受的。通过时间戳可以看到,从启动到计算完成,共花费 32-26=6秒,如果减小模拟次数,可以进一步缩短计算时间,对误差存有少量影响。
以上为蒙特卡洛法计算体积的主要原理,还存有很多需要完善的部分,如,对于每一次生成的随机点,需要判断它在模型的内部还是外部,unity中并没有提供相关的API,因此我自行实现了一个方法,即上图中的 isInside()方法,以下为具体代码:

该方法同样采用了随机的理念来进行判定,原理为:对于一个随机的点,它向着任意方向发射多条射线,若该点存在于模型内,则所有的射线都会打在模型上,若该点在模型外,则至少有一条射线是不与模型碰撞的。
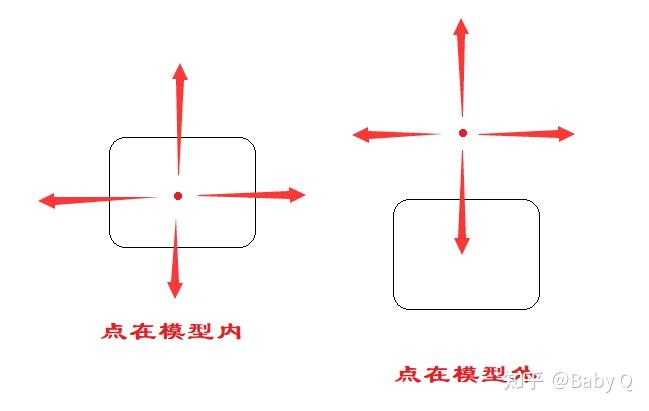
当然,这里涉及到一个问题,如果射线连续多次都打在了模型上,谁能知道下一条射线会不会就没有打到模型呢?这里用概率论简要地解释一下:
对于一个在模型外的点,在它的各个方向中,面对模型的方向,其”视角“通常远小于背向模型的方向。假设打不中的概率是0.6,打中的概率是0.4,对于一个在模型外的点,随机的十次射线都打中模型的概率只有0.4的十次方,即万分之一。
因此,我设定了一个射线次数上限 tryLimit,数值为69,即在69次的随机试验中,如果存有一次射线未打中模型的情况,则返回 false(表明该随机点在模型外),若69次都打中模型了,则返回 true(表明该随机点在模型内)。 over

PS: 经过实际debug测试,tryLimit在39左右即可保存相当的判定精度,但如果你要处理的模型存有很多沟/槽等结构,建议上调 tryLimit到99。
PPS:如果你已经看懂了,就会意识到射线是本方法的核心,但由于unity引擎的预置模型都为单面渲染,导致射线会从内部穿过,因此本文的开头才临时采用plane来进行测试,如果你需要对导入的模型进行处理,就需要将其转为双面显示,读者自行网络学习 shader 相关知识即可。
PPPS:“虚拟球壳”并非必要的手段,如果难以确定导入模型的大致空间范围,可以采用计算AABB包围盒来作为模拟空间,然后利用random.range函数产生三个坐标值,以生成模拟空间内的坐标点,然后进行蒙特卡洛模拟即可。




