压力 q 58.84×10-3 0.33 4220×13.9=0.013228.24×10-5×2257×103×9.81×(958.4-
离心沉降重加降清液抽出,沉降速率1第三重机械分离与固体流态化97中典型的构是由此解出离心沉降速度清液向上停留时间短,则使的卸料




















离心沉降
重加降
清液抽出,
沉降速率
1
第三重机械分离与固体流态化97
中典型的构是由此解出离心沉降速度
清液向上
停留时间短,则使
的卸料锥中
个
Ad(p.-p)w?
个
(3-27)
3pr
加长放隔板
离心加速度a,与重力加速度g之比称为离心分离因数Kc,即
Kea_
n
(3-28)
ggr
工业上Kc值约从几十至几万,因此,同一颗粒在离心场中的沉降速度远大于其重力沉降速度,用离心沉降可将更小的颗粒从流体中分离出来。
颗粒与流体介质的相对运动属于层流时,阻力系数也可用式(3-17)表示,将此式代人式(3-27),简化得
ut一切向速度
u2=18
(3-29)
与式(3-21)对比可知,是用离心加速度u2/y代替了重力加速度g。
四、离心沉降分离设备
(一)旋风分离器
1.构造与操作
查中液
旋风分离器是工业生产中使用很广的除尘设备。它利用离心沉降原理从气流中分离颗
,可以粒。如图3-7所示,其器体上部为圆筒形,下
部为圆锥形。含尘气体从圆筒上侧的进气管以
B
质在切线方向进入,速度为12~25m·s,按螺旋
形路线向器底旋转,接近底部后转而向上,成
净化气体
关。为气芯,从顶部的中央排气管排出。气流中所
夹带的尘粒在随气流旋转的过程中逐渐趋向器
含尘
壁,碰到器壁后落下,自锥形底落入灰斗(未
Di
气体
A=D2
绘出)。但是直径很小的颗粒常在未到达器壁
S
B=D/4
离心
前即被卷入上旋气流而被带出。
D1=D/2
H
因此
在中心轴处可H1=2D
D
旋风分离器内的压力在器壁附近最高,往H2=2D
H
中心逐渐降低,到达气芯处常降为负压,低压S1=D/8
D2≈DA
气芯一直延伸到器底的出灰口。因此,出灰口出K
必须密封完善,以免漏入空气而使收集于锥形
H2
底的灰尘重新卷起,甚至从灰斗中吸进大量
粉尘。
-D2
旋风分离器构造简单,其分离因数约为几
尘粒
十至几百,一般可分离气体中直径5μm以上
图3-7旋风分离器的尺寸及操作原理图
的粒子。
旋风分离器的缺点是对气流的阻力较大,设备和颗粒均易磨损。
旋风分离器各部分的尺寸都有一定比例,图3-7所示为一种类型的尺寸比例。只要规定
出其中一个主要尺寸(直径D或进气口宽度B),则其他各部分的尺寸亦确定。由于气体通
过进气口的速度变动范围不大,以保证其分离效果,故每个尺寸已规定好的旋风分离器所处
理的气体体积流量,亦即其生产能力,可变动的范围较窄。
2.旋风分离器的主要性能
评价旋风分离器性能的主要指标有两个:一是分离性能;二是气体通过时的压降。
整过程过滤阻力几乎不变
第三章机械分离与固体流态化101
流体流过时所引起的挤压与冲撞作用,颗粒紧附在孔道的壁面上(见图3-10)。这种过滤是在过滤介质内部进行的,介质表面无滤饼形成。过滤用的介质为粒状床层或素烧(不上釉的)陶瓷的筒或板。此法适用于从液体中除去很小量(0.1%以下,质量分数)的固体微粒,例如饮用水的净化。悬浮液
悬浮液
原理都与
过滤介质
滤饼
过滤介质
体颗粒从
为较浓的
图3-10深层过滤
图3-11滤饼过滤
戈为向上
2.滤饼过滤
固体颗粒成饼大沉积过滤介质表面
个空的
颗粒的尺寸大多数都比过滤介质的孔道大,过滤时固体物积聚于介质表面,形成滤饼(见图3-11)。过滤开始时,很小的颗粒也会进入介质的孔道内,其情况与深层过滤相同,“架桥钢
部分特别小的颗粒还会通过介质的孔道而不被截留,使滤液仍显得浑浊。在滤饼形成之后,
象
流量的它便成为对其后的颗粒起主要截留作用的介质,滤液因此变清。过滤阻力将随滤饼的加厚而
使较大渐增,滤液滤出的速率亦渐减,故滤饼积聚到一定厚度后,要将其从介质表面上移去。滤饼
底流量过滤方法适用于处理固含量比较大的悬浮液(体积分数在1%以上),可滤出比较多的固体物。化工生产中的过滤多数属于这一种,本节以后的讨论也限于这一种。
交长,
(二)过滤介质
知,
工业上使用的过滤介质应具有下列特性。
旋转
(1)多孔性使液体通过时阻力小,但为了截留住固体颗粒,孔道又不宜大。
了液流
(2)耐腐蚀性、耐热性以适应有相应要求的悬浮液。
(3)有足够的机械强度过滤时要承受一定的压力,且操作中拆装、移动频繁,故应具
织物介质
小颗粒有这一特性。
过滤介质种类繁多,其中以各种天然及合成纤维为原料织造的各种滤布最为常用,此外还有用铜、镍、不锈钢等金属丝织成的平纹或斜纹网。
左右)
用沙砾、碎石、炭屑等堆积成层,亦可作为过滤介质,此外还有各种多孔介质,如多孔
陶瓷、多孔塑料、烧结金属等。新型过滤介质有聚合物膜和无机膜等
(三)滤饼的可压缩性U膜、公0a颗长
某些悬浮液所形成的滤饼,其空隙结构因颗粒坚硬不会因受压(指滤饼两侧的压差)后
不会变形,这种滤饼称为不可压缩的。若滤饼受压后变形,致使滤饼的空隙率(孔隙体积与
滤饼总体积之比)减小而使过滤阻力增大,这种滤饼称为可压缩的颗粒比较软
液中
(四)助滤剂
大方入迟减少阳
被载
若悬浮液中所含的颗粒都很细,刚开始过滤时这些细粒会进入过滤介质而堵塞孔隙,即
使并未严重到如此程度,这些很细的颗粒所形成的滤饼对液体的透过性也很差,即阻力很
普遍
大,使后续的过滤困难。又若滤饼具有明显的可压缩性,也将使过滤阻力大为增加。采用助滤剂可以减轻上述困难。助滤剂是颗粒细小且粒度分布范围较窄,坚硬而悬浮性
好的颗粒状或纤维状物质。助滤剂能形成结构疏松、而且几乎是不可压缩的滤饼。常用作助
滤剂的物质有:硅藻土,这是一种单细胞水生植物的沉积化石,经过干燥或煅烧,含85%
以上的二氧化硅;珍珠岩,将一种玻璃状的火山岩熔融后喷入水中,得到中空的小球,再打
100花工原理
BD-D03D
核
838×0.4=0.15m
22
2
流体流过时所引起的挤压
dip(8.0×10-6)2×2300×13.92
18×3.6×105×0.15=0.29ms
在过滤介质内部进行的,
u18urm
的)陶瓷的简或板。此法
deup8.0×10-×0. 29×0.46=0.029(<2)
例如饮用水的净化。悬浮液
Reo=
3.6×105
可见颗粒沉降服从斯托克斯公式,上述计算有效。
(二)旋液分离器
旋液分离器是一种利用离心力从液流中分离固体颗粒的设备。其构造及操作原
风分离器基本上相同。图3-9所示为这种设备的简图。
D
旋液分离器不能将固体颗粒与液体介质完全分开。固体
图3-10
D
旋液流中甩到器壁上后,随液流下降到锥形底的出口,成为较
浮液排出,称为底流。清液或只含有很细颗粒的液体,则成为
2.滤饼过滤
颗粒的尺寸大多
内旋流经中心管排出,称为溢流。内层旋流中心还有一个
气芯。
(见图3-11)。过滤开
调节旋液分离器底部出口的开度,可以调节底流量与溢流影部分特别小的颗粒还
例,从而使几乎全部或者仅使一部分固体颗粒从底流送出,使它便成为对其后的
较小直径的颗粒分别从底流、溢流中送出的过程称为分级。底流渐增,滤液滤出的
过滤方法适用于处
溢流量之比的调节,还可以控制两部分中颗粒大小的范围。
物。化工生产中的
旋液分离器的直径与旋风分离器相比较小,而锥形部分较长
(二)过滤介
Du
原因在于固、液密度差较固、气密度差小,根据式(3-27)可知
工业上使用的
图3-9旋液
想在一定的进口切线速度下,维持足够大的沉降速度,应缩小旋
(1)多孔性
分离器简图
径;这样做还可减少沉降时间。而加大锥形部分的高度则增大了
(2)耐腐蚀
的行程,从而停留时间更长。
(3)有足够
旋液分离器往往是很多个做成一组来使用。它可从液流中分出直径为几微米的小有这一特性。
但它作为分级设备的应用更为广泛。
过滤介质种
由于圆筒直径小(常见的范围为50~300mm),液体进口速度大(可达10m·s左还有用铜、镍、
用沙砾、
故阻力损失很大,磨损也较严重
陶瓷、多孔塑
过滤常为沉降的后续操作
(三)滤
第三节过滤
某些悬浮
不会变形,这
一、概述
在外力作用下
滤饼总体积之
过滤是利用多孔介质(称为过滤介质),使液体通过而截留固体颗粒,从而使悬浮
(四)助
的固、液得到分离的过程。原始的悬浮液称为滤浆,通过多孔介质后的液体称为滤液,
若悬浮
留住的固体颗粒堆积层称为滤渣或滤饼(其空隙中充满滤液)
使并未严重
驱使液体通过过滤介质的推动力,有重力、压力和离心力。本节着重讨论应用最为
大,使后续
的压力过滤,而以离心力为推动力的过滤将在第四节中介绍。
采用助
(一)深层过滤和滤饼过滤
好的颗粒状
工业上的过滤方法主要有以下两种。
滤剂的物
1.深层过滤
以上的二
颗粒尺寸比介质的孔道小得多,但孔道弯曲细长,颗粒进人之后仍容易被截住,还
为临界直径d
得:①气体在
旋液分离器
中所穿过的气流
第三章机械分离与固体流态化99
结构特点:直径小而圆锥部分长
了略去;又用进
10
D
8
0.7
0.6
0.5
0.4
0.3
0.2
---理论
停留时间
实际
0.1
B
0.20.30.40.50.60.81.0
2
345678910
离出来,因此
颗粒直径比dde
间的表达式
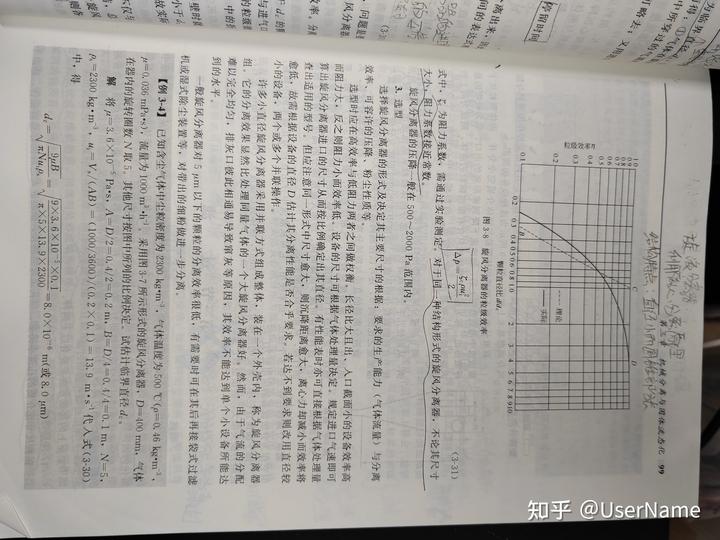
图3-8旋风分离器的粒级效率
器的进
LAn-
(3-31)
式中,为阻力系数,需通过实验测定。对于同一种结构形式的旋风分离器,不论其尺寸
的本
大小,阻力系数接近常数。
好
旋风分离器的压降一般在500~2000Pa范围内。
3.选型
(3-30)
选择旋风分离器的形式及决定其主要尺寸的根据:要求的生产能力(气体流量)与分离
问题
效率、可容许的压降、粉尘性质等。
风分离器
选型时应在高效率与低阻力两者之间做权衡。长径比大且出、入口截面小的设备效率高而阻力大,反之则阻力小而效率低。设备的尺寸可根据气体处理量决定。规定进口气速即可
率。分离
算出旋风分离器进口的尺寸从而按比例确定出其直径。有性能表时亦可直接根据气体处理量查出适用的型号。但应注意同一形式中尺寸愈大,则沉降距离愈大,离心力却减小而效率将愈低,故需根据设备的直径D估计其分离性能是否合乎要求。若达不到要求则改用直径较
Fde的颗
小的设备,两个或多个并联操作。
与进气
许多小直径旋风分离器采用并联方式组成整体,装在一个外壳内,称为旋风分离器
的粒级效
组。它的分离效果显然比处理同量气体的一个大旋风分离器好。然而,由于气流的分配
中的折
难以完全均匀,排灰口彼此相通易导致窜灰等原因,其效率不能达到单个小设备所能达到的水平。
壁时就
一般旋风分离器对5μm以下的颗粒的分离效率很低,有需要时可在其后再接袋式过滤
小于d
机或湿式除尘装置等,对带出的细粉做进一步分离。
故实际
【例3-4】已知含尘气体中尘粒密度为2300kg·m3,气体温度为500℃(p=0.46kg·m3μ=0.036 mPa•s),流量为1000 m3·h1。采用图3-7所示形式的旋风分离器,D=400 mm,气体
仅与
在器内的旋转圈数N取5。其他尺寸按图中所列的比例决定。试估计临界直径d。
,总
解将μ=3.6×105Pa•s, A=D/2=0.4/2=0.2m,B=D/4=0.4/4=0.1m,N=5,
旋风
p=2300 kg•m3,u=V3/(AB)=(1000/3600)/(0.2×0.1)=13.9 m·sl代人式(3-30)
则各
中,得
de:9ub
9×3.6×10-5×0.1
Nup
X5×13.9×2300=8.0×10-6m(或8.0μm)
102化工原理
使用间的得到较清洁的滤
碎而成;此外还有炭粉、纤维素等
助滤剂施用的方法有二。一是配成悬浮液先在过滤介质表面滤出一薄层血
滤饼,然后进行正式过滤。此法称为预涂,可以防止滤布孔道被微细的颗粒
开始就得到澄清的滤液;在滤饼有胶黏性时,亦易于从滤布上取下。二是将
中,所得到的滤饼将有一较坚硬的骨架,压缩性减小,孔隙率增大。但若过的
固体物又不允许混入助滤剂,此法便不适用。只有悬浮液中的固体量少又可
剂用量不大时,使用此方法比较经济合理。
二、过滤设备
工业上应用最广的过滤设备是以压力(压差)为推动力的过滤机,典型的有
(a)非洗涤板
滤机(以上为间歇式)和转筒过滤机(连续式),分述如下。
(一)压滤机
1一悬浮液通道:2一洗涤
压滤机以板框式最为普遍,它是由许多交替排列在水平支架上并可在支架上
和滤框所构成(见图3-12)。
所示,洗涤用的清水经洗涤极
暗流式
另一侧的滤布,经过非洗涤
进入卸渣、整理阶段,即将
流式
开始。
滤浆→
悬浮液
板过滤板(一纽)
入口
洗涤板(三纽)
板与板之间,加入框
滤液
进行组合(二)
9
8
图3-12板框式压滤机简图(暗流式)
1一固定机头;2-滤布;3-滤板;4-滤框;5滑动机头;6一机架;
7一滑动机头板;8一固定机头板;9一机头连接机构
板与框的形状如图3-13所示。滤框和滤板的左上角与右上角均有孔,滤框右上角
压滤机的板、框可
有小通道与框内的空间相通(如箭头所示),滤浆可由此进入。滤板又分成两种,图300.3~0.5MPa。我国
所示为非洗涤板,图3-13(c)所示为洗涤板。洗涤板的特点是左上角的孔还有小通道与1000mm。框的数目可
两侧相通,洗涤液可以由此进入(如箭头所示)。为了便于区别,在板与框边上做不同的
板框压滤机的优
非洗涤板以一为记,洗涤板以三为记,而框则用两钮,见图3-13,板框压机通过板1.5MPa),便于用耐
所用的劳动量多而且
上的道,或板与两侧出的通加料和排出液的排出方为明
近年大型压滤
装置自动压紧或拉
查滤液质量;暗流压滤机的滤液在机内汇集后由总管排出机外(见图3-12)。对于滤液易或含有有毒气体的悬浮液的过滤需用暗流。
力作用而自行落下
除附着在滤布上的
板框压滤机的操作是间歇的,每个操作循环由装合、过滤、洗涤、卸渣、整理五个
(二)叶滤机
组成。装合时,将板与框交替地置于机架上,板的两侧用滤布包起(滤布上亦根据板、框
叶滤机由许多
架(见图3-15),
中的液体在压力作
的小孔道进入框内[见图3-14(a)],滤液穿过滤布到达板侧,沿板面流动,然后排出。改充清水,使水循
物则积存于框内形成滤饼,直到整个框的空处都填满为止。滤饼的洗涤方式如图3-14其脱落,或用压
算层由助滤剂
粒堵死,并
第三章机械分离与固体流态化103
将助滤剂加
过滤的目的
可弃去,而且
5
。
的有压滤机
(a)非洗涤板
(b)滤框
(c)洗涤板
图3-13滤板和滤框
洗涤水穿过途径是过渡终
架上滑动的
1一悬浮液通道;2洗涤液人口通道;3一滤液通道;4洗涤液出口通道;5一用于标识的钮了日时打老社
所示,洗涤用的清水经洗涤板上角的斜孔进入板侧,穿过滤布到达滤框,再穿过整个滤饼及另一侧的滤布,经过非洗涤板流动而排出,此种洗涤方式称为横穿洗法。洗涤阶段结束后,
途径的两
进入卸渣、整理阶段,即将滑动机头松开,取出滤饼并清洗滤布及板、框,准备下一循环开始。
悬浮液
入口
洗涤水
入口
滤液流出
洗涤水流出
(a)过滤阶段
(b)洗涤阶段
1一板;2一框
1一非洗涤板:2一框:3一洗涤板
图3-14板框压滤机的过滤和洗涤
压滤机的板、框可用铸铁、碳钢、不锈钢、铝、塑料、木材制造,操作压力一般为
角的
0.3~0.5MPa。我国制定的压滤机规格系列中,框的厚度为25~50mm,框每边长320~
3-13(
1000mm。框的数目可自几块到50块以上,随生产能力而定。
板面
板框压滤机的优点是构造简单,过滤面积大且占地省,过滤压力高(压差可达
的标记
1.5 MPa),便于用耐腐蚀材料制造,所得滤饼含水量少且能进行洗涤。它的主要缺点在于
板所用的劳动量多而且劳动强度大,一般适用于中小规模的生产及有特殊要求的场合。
和
近年大型压滤机的机械化与自动化发展很快,节省了劳动量。滤板及滤框可由液压装置自动压紧或拉开,全部滤布连成传送带式,运转时可将滤饼从框中带出使之受重
需检
力作用而自行落下。又有一种设计能在拉开滤框的同时将滤布拉出,借助于振动器清
挥发
除附着在滤布上的滤渣。
(二)叶滤机
阶段
叶滤机由许多滤吐组成,滤叶可以垂直放置亦可水平放置。滤叶为金属网围成的扁平框
框角
架(见图3-15),外包滤布。将滤叶装在密闭的机壳内(见图3-16),为滤浆所浸没。滤浆
框
中的液体在压力作用下穿过滤布进入滤叶内部,成为滤液从其周边引出。过滤完毕,机壳内
内
改充清水,使水循着与滤液相同的路径通过滤饼,进行置换洗涤。最后,滤饼可用振动器使
体
其脱落,或用压缩空气将其吹下。
b)
过管道分别与滤液罐、洗水罐(1
通(见图3-19),当转动盘上的某
滤饼
的几段便与滤液罐接通滤液可
滤叶
过40~60mm,对于难以过滤的
个小孔与凹槽相遇的,相应的
滤液
风机,空气吹向转的这部分
又被刮刀刮下。这部分表面再
洗水路
动盘上的小孔与固定盘两凹槽
与之相对应的段停止操作,以
滤液
波相同
周,过滤表面的任一部分都顺
对于任一部分表面来说,都
部分表面分别进行着不同阶
图3-15叶滤机的构造
置换洗法
图3-16密闭加压叶滤机
悬浮液
吐滤机也是间歇操作设备,它具有过滤推动力大,单位地面所容纳的过滤面积大涤较充分等优点。其生产能力可以比板框压滤机大,而且机械化程度较高,劳动加
洗水泵
密闭过滤,操作环境亦较好。其缺点是构造较为复杂,造价较高,而且滤饼中粒度差的颗粒可能分别积聚于不同的高度,使洗涤不易均匀。
(三)转筒真空过滤机
这是工业上应用很广的一种连续操作的真空过滤机。其主要部件为转筒,其长度之比为1/2~2,筒壁上覆盖有金属网,滤布支承在网上。浸没于滤浆中的过滤面积约部面积的30%~40%,转速为0.1~3r·min。
转筒的构造如图3-17所示。筒壁按周边平分为若干段(图中为14段),各段均有至轴心处(图中示出一段的连通管),但各段在筒内并不相通。圆筒的一端有分配头装心处,分配头由一个与转筒连在一起的转动盘和一个与之紧密贴合的固定盘组成,分图3-18(a)、(b)所示。转动盘上的每一孔各与转筒表面的一段相通。固定盘上有三个凹槽
转筒表面所形成
滤布
转鼓表面的整个宽度
支承网
表面,将滤饼带出
洗涤区
联通管
我国制定的转
转筒过滤机的
分配头的
过渡
下便嫌小。由于采
转动盘
堵头吹气以助卸渣刮刀
的滤饼洗涤亦不够
o
转筒的过滤
过滤区
o
o
o
体颗粒粗细不等
o
o
若将圆筒改
滤浆平面
旋转方向
ooo
一根轴上可以安
2
滤浆槽
(a)转动盘
(b)固定盘
法进行。
图3-17转筒
图3-18转筒的分配头
三、过滤
1一与筒壁各段相通的孔;2,3一与真空管路
前已述及
相通的凹槽;4一与吹气管路相通的凹槽
过程
过滤速度
过滤速度指单位时间内通过单位过滤面积的滤液体积,用符号a表示。由于
定过程,需用微分式表示其瞬时过滤速度
滤饼内,雷诺
滤液通过滤
式中,u为瞬时过滤速度,m3•m2•s1,即m•s;V为滤液体积,m2;A为过面
q为单位过滤面积所得的滤液体积,m2·m2,q=V/A;0为过滤时间,s
u=dVdq
(二)过滤基本方程
Ado do
式(3-35)称为康采尼
过滤时,滤液在滤饼与过滤介质中的微小通道中流动,由于通道形状很不规则
联,难以对流体流动规律进行理论分析,故常将真实流动[参见图3-20(a)]简化
为1。的一组平行细管中的流动[图3-20(b)],并规定:
,称为滤饼的比阻
①细管的内表面积之和等于滤饼内颗粒的全部表面积;
(几乎所有的滤饼都是
式(3-36)表明,
②细管的全部流动空间等于滤饼内的全部空隙体积。
的压力差△p1,即过滤
细管
由两方面的因素决定:
明,滤饼不可压缩时,
比。故式(3-36)也可
以上推导过程仅
则可将两者阻力相加
写成
(a)滤饼
de
u
(b)简化模型
图3-20流体在滤饼中流动的简化模型
式中,△P2
为通过过
根据上述假定,可求得图3-20(b)中这些虚拟细管的当量直径d。
△P1+△P2。
过滤时,滤饼厚
de=4×流通截面积
在过滤介质上被截
上式分子、分母同乘以细管长度,则有润湿周边长
渣体积为cV,而滤
d e=4×细管的流动空间4Elk
细管的全部内表面积Dol
或
令滤饼的体积为V,其空隙率为e(空隙体积/滤饼体积),滤饼的比表面为a
体积的滤饼层所具有的颗粒表面积),如果忽略颗粒因相互接触而使裸露的表面减少,对于过滤介质
与颗粒的比表面a的关系为aB=a(1-e)。
式中,V。为滤出
故根据上述假定可知,细管的流动空间=eV,细管的全部内表面积=aBV=a(1-
值得注意的是
Au =Acu,
特性。
u1=
de=-4E
综合上述推理
a(1-e)
(3
由于饼的微小通道的直径很小,阻力很大,因而这时液体的流亦很小,常流,故可用第一章的哈根-泊谡叶公式[式(1-37)]计算虚拟细管中的阻力损失
若需要考虑
需通过实验求出
△p1=△p1=32uleui
e
式中,△p1为通过滤饼的压降,Pa;u1
d
32mle
(3-3式中,
单位
s均光
为滤液在虚拟细管中的流速,m•sl,根据连续可知u1=u/e;u为滤液的黏度,Pas;l2为细管长度,m,与滤饼厚度L具有一定的
可压缩滤饼,s
例关系,令l=KL,K。为无量纲的比例常数。
将式(3-33)及u1=u/e和l=KoL代入式(3-34),整理得
物料
硅
5
0.
第三章机械分离与固体流态化105
过管道分别与滤液罐、洗水罐(以上二者均处于真空之下)及鼓风机贮气罐(正压下)相连通(见图3-19)。当转动盘上的某几个孔与固定盘上的凹槽相遇时,转筒表面与这些孔相连的几段便与滤液罐接通,滤液可从这几段吸入,同时滤饼即沉积于其上。滤饼厚度一般不超过40~60mm。对于难以过滤的胶质滤浆,厚度可小至10mm以下。当转动盘转到使这几个小孔与凹槽相遇的,相应的几段表面便与洗水罐接通,吸入洗水。与凹槽4相遇则接通鼓风机,空气吹向转鼓的这部分表面,将沉积于其上的滤饼吹松。随着转筒的转动,这些滤饼又被刮刀刮下。这部分表面再往前转便重新浸人滤浆中,开始进行下一个操作循环。每当转动盘上的小孔与固定盘两凹槽之间的空白位置(与外界不相通的部分)相遇时,则转筒表面与之相对应的段停止操作,以便在操作区间转换时不致互相串通。通过分配头,每旋转一周,过滤表面的任一部分都顺序经历过滤洗涤、吹松、刮渣等阶段。因此,每旋转一周,对于任一部分表面来说,都经历了一个操作循环而任何瞬间,对于整个转筒来说,则其各部分表面分别进行着不同阶段的操作。
吸干
洗水喷头
吹气口
悬浮液
转筒
大,
除沫器
四.心式包
滤饼
力较
别较
洗水泵
与直
占
真空罐
洗水
滤液
空气真空泵
管通
于轴
泵
大气密封
别如
图3-19转筒真空过滤机的操作流程
转筒表面所形成的滤饼厚度一般不大,有时用刮刀卸料易损坏滤布,可改用绳索卸料:转鼓表面的整个宽度上都绕有许多圈环状的绳,滤渣形成后附于其上,卸料处绳索离开转鼓表面,将滤饼带出。
我国制定的转筒真空过滤机规格系列中,转筒的直径为1~3m,过滤面积为2~50m2。转筒过滤机的突出优点是操作连续、自动,其缺点是转筒体积庞大而其过滤面积相形之下便嫌小。由于采用真空吸液,过滤的推动力不大,悬浮液温度不能高。此外,转筒过滤机的滤饼洗涤亦不够充分。然而,它对于大规模处理固含量很大的悬浮液,是很适用的。转筒的过滤表面还可以设在筒内,悬浮液送入后随筒旋转,称为内滤式,适用于其中固体颗粒粗细不等且易于沉淀的悬浮液,但其结构较复杂。
若将圆筒改为绕水平轴旋转的圆盘,过滤表面位于盘的两侧,则成为转盘过滤机。由于
一根轴上可以安装2~8个圆盘,故过滤面紧凑得多,但构造也复杂得多,滤饼的洗涤亦无
法进行。
三、过滤的基本理论
前已述及,滤饼过滤过程中,滤饼逐渐增厚,流动阻力也随之逐渐增大,所以过滤过程
滤饼内,雷诺数小,屋层次流动
滤液通过滤饼的理论压降二滤饼外界上下两侧的压强差
于过滤为
第三章机械分离与固体流态化·107
dV
子
△P1
(3-35)
uAd0 2Koa2(1-e)2μL
式(3-35)称为康采尼(Kozeny)式。令
0
虑面积,
m2,则
2Ko e
2Koa2(1-c)
YC
dv_△p1
(3-36)
u-AdoμrL
,称为滤饼的比阻,与颗粒的比表面积、滤饼的空隙率等特性有关。对于不可压缩滤饼
则且相互(几乎所有的滤饼都是可压缩的,但压缩性很小的,常当作不可压缩的来处理),r为常数。
乙成长度
式(3-36)表明,瞬时过滤速度的大小由两个相互抗衡的因素决定:一为促使滤液流动的压力差△p1,即过滤推动力;另一为阻碍滤液流动的因素rL,相当于过滤阻力。后者又由两方面的因素决定:一是滤液的黏度μ;二是滤饼的特性r及其厚度L。式(3-36)还表明,滤饼不可压缩时,瞬时过滤速度与滤饼两侧的压差成正比,与其厚度、滤液黏度成反比。故式(3-36)也可写成
dV_过滤推动力
(3-36a)
Ad0过滤阻力
以上推导过程仅考虑了滤饼层对过滤的影响,而朱考虑到过滤介质,若两者都加以考虑,则可将两者阻力相加。为计算方便,将介质阻力折合成厚度为L。的滤饼阻力,式(3-36)改写成
若考皮波
dV△pi△p2 Ap
过滤总推动
二
(3-37)
A do urL urLe ur(L+Le)(滤饼阻力+介质助)
式中,△p2为通过过滤介质的压降,Pa;△p为通过滤饼和过滤介质的总压降,Pa,Ap=△p1+△P2。
过滤时,滤饼厚度L随时间而增加,滤液量亦成比例增多。如果获得单位体积滤液时,在过滤介质上被截留的滤饼体积为c(m3滤饼·m3滤液),则得到的滤液为V时,截留的滤渣体积为cV,而滤渣层厚度为L,则滤渣体积
cV=AL
或
对滤饼
(3-38)
对于过滤介质
L一
(3-39)
式中,V。为滤出厚度为L。的一层滤饼所获得的滤液体积。
值得注意的是,V。实际并不存在,而是一个虚拟的量,其值取决于过滤介质与滤饼的特性。
综合上述推理,式(3-37)可写成dV△pA
(3-40)
Ad0 urc(V+Ve)
若需要考虑滤饼的可压缩性,应计人比阻r随过滤压力的变化。比阻与过滤压力的关系需通过实验求出,其结果多整理成下列形式的经验公式
单位下比阻,
par=roAp
(3-41)
式中,(
、s均为实验常数。其中s称为压缩指数,滤饼的可压缩性愈大,值愈大。对于不可压缩滤饼,s=0。表3-2列出了几种典型物料s的数值,以供参考。
表3-2典型物料的压缩指数
物料
硅藻土
碳酸钙
钛白(絮凝)
高岭土
滑石
黏土
硫化锌氢氧化铝
0.01
0.19
0.27
0.33
0.510.56~0.60.69
0.9
理
(一)洗涤速度
de
Aap's
洗涤速度用(dV/Ad)。表示,单位m/s。洗涤液在滤饼中的流动过程与过滤似,因此
cpAr'Ltley
can
洗涤阻力与过滤阻力类似,与滤饼的比阻、洗涤液黏度、滤饼厚度、介质阻力有
dv
当洗涤压力与最终过滤时的操作压力相同时,则洗涤速度(dV/Ad0)。与最终
A do).洗涤推动力
滤与洗涤所占的时间都因产
(dV/Ad0)。之间有如下关系
w洗涤阻力
作循环中过滤时间短,则
Ltle)-2LtLele
大,此时生产能力不一定
也不一定大。所以,一个
Awi
滤时间内生成的滤饼厚度
式(3-51)还可改写成洗涤速率、最终过滤速率之比的形式
()()
叶片之间距离的根据。
要求最佳操作周期及
为简单计,略去滤布阻大
(器)/(),-造气
式中,μ、μ分别为滤液、洗涤液的黏度;A、L分别为过滤面积和最终过滤时的度;A、L分别为洗涤面积和洗涤时通过的滤饼厚度。
因一个循环的滤液
(3滤液量V成正比,即
对于板框压滤机,属横穿洗法,即洗涤液所穿过的滤饼厚度2倍于最终过滤时滤过的厚度,而洗涤液的流通截面却只有滤液的流通截面的一半,假定洗涤液的黏度与式中,J为比例系数,
度相等,则洗涤速率(dV/d0)只有最终过滤速率(dV/d0)。的1/4。
再忽略洗涤液黏度
8=1,横穿洗法=1
对于叶滤机和转筒真空过滤机,属置换洗法,洗涤液所走的路线与最终过滤时滤
线是一样的,故黏度相同时,洗涤速率(dV/d)等于最终过滤速率(dV/d。
利用式(3-51a)及式(3-43),可由最终过滤速率求出洗涤速率。实际洗涤操作中可能故洗涤时间为
因滤饼开裂而发生沟流、短路等现象,使洗涤速率比按式(3-51a)的计算值大
(二)洗涤时间0
将式(3-55)、式(3-5
设洗涤液用量为Vw,则洗涤时间
0n=vn/()
式(3-57)中的
五、生产能力
(3
了求Q的最大值,
利用过滤方程式,以及通过实验或从生产设备上取得的过滤常数数据,便可计算过
的生产能力,或过滤面积。
这表明,在过
各种类型过滤机在构造和操作方式上各有其特点,在过滤计算中要结合设备的这些
时,间歇过滤机的
进行。下面将对间歇式和连续式两种类型的过滤机分别讨论。
(一)间歇过滤机
1.操作周期及生产能力
【例3-6】
间歇过滤机的一个操作周期包括过滤时间0、洗涤时间0、卸渣、重装等辅助时间,
过滤常数为:K
c=0.08m3·m
0c=0+0w+0
(3-5
式中,0可采用恒压过滤方程式计算;0采用式(3-52)计算;0由生产实际情况而定,
试验时相同。
过滤及洗涤的速率无关。
33m2,框内总
间歇过滤机的生产能力是指一个操作周期内获得的滤液量或滤饼量设一个提作
时间;(2)过
获得的滤液量为V,则生产能力可表示为
e.但上
清理、重装等
积计。
,+0n
V
Q可到
(3-54
解该压
2.最佳操作周期及最大生产能力
过滤面积
一个操作循环中,过滤装置拆卸、整理与重装等辅助时间是固定的,与产量无关;耐
框内总
-pl
第三章机械分离与固体流态化109
(3-
+
(3-43再将上式中的微分用差分代替
O=20
(3-49)
△q
K
其中,实验中测出0与q的对应值之后,算出各时间段△0内的△q;将△0/△q对q作图,所得直线的斜率为2/K,截距为2q/K。以上两种方法所得结果相同。
用上述方法还可以测出不同恒压差△p下的K值,再根据K与△p的关系[式(3-42)],有
lgK=(1-s)lg△p+B
斜率为()
不同条
可见lgK与lg△p成直线关系,由直线的斜率可求出压缩指数s。截距B=1g[21(rcN]]
个过程
【例3-5】CaCO3粉末与水的悬浮液在恒定压差117 kPa及25℃下进行过滤,实验
亦会超
结果见表3-3,过滤面积为400cm2,求此压差下的过滤常数K和qe。
塞介
表3-3恒压过滤实验中的0-V数据
开始
过滤时间0/s
6.8
19.0
34.5
53.4
76.0
102.0
玉阀被
滤液体积V/L
0.5
1.0
1.5
2.0
2.5
3.0
总地来
解利用q=V/A将表3-3中的数据整理成表3-4。
表3-4q与0/q的关系
常数
0/s
6.8
19.0
34.5
53.4
76.0
102.0
3-43)
0.075
q/m3·m-2
0.0125
0.025
0.0375
0.05
0.0625
/sm
544.0
760.0
920.0
1068.0
1216.0
1360.0
3-44
3-45)
将0/q与q的关系绘成图3-21,得一直线,从图中求得
1500
-46)
1000
-47)
500
过滤
0.025
0.05
0.075
同
q
要
图3-21例3-5附图
等
斜率=12900s·m2,距=410s*m
故
K=7.75×10-5m2s-1
9=×410=0.016m3·m2
四、滤饼洗涤
.回收带写在滤款健女
滤饼洗涤时,洗涤液(通常是水)所通过的滤饼厚度不增厚,因此,洗涤时的流动阻力
不变,故恒压下的洗涤过程属于稳定流动过程
得将式(3-41)代入式(3-40),并令A e)
女
影响K的
或
1
K
0
2p-
滤饼性
dv
roC
式中
do
KA2
2滤浆性质
qe=Ve/A
2(V+y)
dq
回推动力()
K
式(3-43)、式(3-43a)是过滤基本方程的微分式,表示任一瞬间的过滤速率。其
do2(9+ge)
再将上式中的微分用差分代
qe(或V。)通常称为过滤常数,其值需由实验测定
(三)恒压过滤方程式
实验中测出0与q的对应值
要将式(3-43)、式(3-43a)用于过滤计算,还要按照具体条件积分。
连续过滤和间题过滤常用方法
的斜率为2/K,截距为2q。
用上述方法还可以测出
间歇式过滤机(以板框压滤机为代表)的操作可以在恒压、恒速或变速变压等不
下进行。然而,工业过滤并不宜于使整个过程全部在恒速或恒压下进行。若要使整个可见gK与lg△p成
维持恒速,则过程末期的压力要升到很高。这时过滤机易产生泄漏,泵的带动设备会
【例3-5】CaCO3
荷。严格地维持恒压则因刚开始时介质表面并无滤渣,猛然加压会使较细的颗粒堵寨结果见表3-3,过滤面积
孔隙而增大其阻力。常用的操作方式是在供料泵出口安装支线,支线上有泄压阀,开始
时有一短的升压阶段,在此期间的过滤既非恒压亦非恒速,压力升到一定数值,泄压
过滤时间0/s
开,从支线泄去一部分悬浮液,此后过滤便大体上在恒压下进行。
滤液体积V/L
至于连续过滤机(以转筒真空过滤机为代表),则都是在恒压条件下操作。所以总
解利用q=V/
说,恒压过滤还是占主要地位,故下面重点讨论恒压过滤的计算。
恒压过滤时,过滤压力恒定。对于一定的悬浮液,μ、ro、c亦为常数,故K为
这样,可将K提到积分号之外。从过滤开始(0=0)到过滤结束(6时刻),积分式(3
0/s
式(3-43a)得
q/m3·m-2
/s·m
0
V2+2VVe=KA20
(3
或者
q2+2qq=K0
将θ/q与q的
(3
若过滤介质阻力可忽略不计,则以上两式简化为
V=KA20
(3
12=K0
(34
(四)过滤常数的测定
过滤计算要有过滤常数K、q。(或V。)作为依据。由不同物料形成的悬浮液,其
常数差别很大。即使是同一种物料,由于浓度不同,存放时发生聚结、絮凝等的条件不
其过滤常数亦不尽相等,故要有可靠的实验数据作为参考,才能做出有把握的设计。但题
注意,由于小型设备与大型设备之间,滤饼沉积的方式、饼的均匀程度、机械构造的影
方面都有区别,故据此做出的设计,仍要采用相当大的安全系数(25%以上)。下面说明如何通过实验测定过滤常数。
斜率=
由恒压过滤方程式(3-45)得
故
0K92
(3-48
式(3-48)表明,恒压过滤时0/q与q之间为线性关系。故实验中只要得出不同过滤
间0内的单位面积滤液量q,将0/q对q作图,便可得一直线,其斜率为1/K,而截
四、滤饼
滤饼洗涤
2qe/K。
不变,故恒
或者将式(3-43a)改写成以下形式
过滤过
第三章机械分离与固体流态化111
滤与洗涤所占的时间都因产量(以所得的滤液体积或滤饼体积计)的增加而增加。若一个操(3-5
力有关作循环中过滤时间短,则所形成的滤饼薄,过滤的平均速率便大,但其辅助时间所占的比例
过滤速大,此时生产能力不一定大。反之,过滤时间延长则滤饼厚,过滤的平均速率小,生产能力也不一定大。所以,一个周期内过滤时间应有一最佳值,使生产能力达到最大。在此最佳过滤时间内生成的滤饼厚度,应是设计压滤机时决定最适宜框厚的根据,亦是决定叶滤机内两
叶片之间距离的根据。
(3-51
要求最佳操作周期及最大生产能力,可将式(3-54)对V求导数,并令导数等于零求得。
为简单计,略去滤布阻力。由式(3-46)可知
0=
2
(3-51a
KAz
(3-55)
滤饼厚
因一个循环的滤液量愈多,则滤饼愈厚,洗涤用水量也应愈多,故可设洗涤液量V与滤液量V成正比,即
式中,J为比例系数,无量纲。
Vw=JV
液所通
滤液裂
再忽略洗涤液黏度与滤液黏度的差别,则洗涤速率为最终过滤速率的δ倍(置换洗法δ=1,横穿洗法δ=1/4)。即
的路
(酱)-o(酱)-o
故洗涤时间为
能会
V2JV
w(av/do)w oKA2
(3-56)
将式(3-55)、式(3-56)代入式(3-54),得
V
Qy2/KA2+2JV2/6KA2+0R
(3-57)
式(3-57)中的K、J、δ为常数,0由工作情况而定亦为常数,故只有一个变量V。为了求Q的最大值,可令dQ/dV=0而得到
O2+
2JV2=0+0、
KA2
(3-58)
这表明,在过滤介质阻力忽略不计的条件下,当过滤时间与洗涤时间之和等于辅助时间时,间歇过滤机的生产能力最大,此即为最佳操作周期
0c.opt-0+0w+0R-20R
ray-(3-59)
【例3-6】在试验装置中过滤钛白(TiO2)的水悬浮液,过滤压力为0.3MPa,测得过滤常数为:K=5×10~5m2·sl,q=0.01m3·m2。又测出滤饼体积与滤液体积之比c=0.08m3·m3。现要用工业型板框压滤机过滤同样的料液,过滤压力、所用的滤布亦与试验时相同。滤框长与宽均为810mm,厚度为45mm,共有26个框,过滤面积为33m2,框内总容量为0.760m3。试计算:(1)过滤进行到框内全部充满滤饼所需的过滤时间;(2)过滤后用总滤液量体积的1/10清水进行洗涤,求洗涤时间;(3)洗涤后卸渣、清理、重装等共需40min,求每台压滤机的生产能力,以平均每小时可得到的滤饼体积计。
解该压滤机的过滤面积与框内容量已列出,现核算如下。
过滤面积=框长×框宽×框数×2=0.81×0.81×26×2=34.1m
框内总容积=框长×框宽×框厚×框数=0.81×0.81×0.045×26=0.768m3
计算值略大于题中的给定值,系由于计算中未考虑框上悬浮液通道与洗水通道位置。后面的计算按题中给定值进行,
(1)滤框充满的过滤时间
滤框全部充满滤饼时得到的滤液量
单位面积的滤液量
V=
此即为最佳滤框厚度。
框内总容积_0.760≥9.5m2
其生产能力可计算如下。
将q值及题中所给的过滤常数代入恒压过滤方程式(3-45)中
C
V9.5
0.08
95
A
33=0.288m3·m2
可见,最佳生产能力较例
0.2882+2×0.288×0.01=5×1060
(二)连续过滤机
(2)过滤后用总滤液量体积的1/10清水进行洗涤,求洗涤时间
0=1774s(或29.6 min)
1.操作周期
以转简真空过滤机为
秒钟n次,则操作周期便
洗涤液量Vw=1V=0.95m3
最终过滤速率(d0)。2(V+Ve)2(q+qe) 2×(0.288+0.01)
dv
KA2
KA
转简真空过滤机在整
5×105×33
板框压滤机属横穿洗涤,洗涤速率
=2.77×103m3面积只在部分时间内进
()_-()-×2.77×10-3=6.93×104m3g
则过滤的部分面积就是
洗涤时间
Vw
2.生产能力
0w(dv/d0)w6.93×104
0.95=1371s(或22.9 min)
根据恒压过滤方程
(3)生产能力,以平均每小时可得到的滤饼体积计
滤液量为V=A√Kθ=
已知辅助时间0R=40min
操作周期0=0+0+0R=29.6+22.9+40=92.5 min(或1.54 h)
故
式(3-62)表明,
生产能力=0.760/1.54=0.49m3(滤饼)h
一定限制:若转速过
【例3-7】例3-6的压滤机的框稍嫌厚,若充满框才停止过滤,则过滤时间稍长,高,则洗涤、吸干、
【例3-8】例3
有达到最佳化的要求。试求每周期最佳的滤液量与滤饼厚度,及可达到的最大生产能加解因ge/q=0.01/0.288=0.035,故本题可略去滤布阻力以简化计算。由式(3-56)
关参数为:转筒直径
入角度为90°~133
020
度为70kPa,若滤
本题中J=1/10,δ=1/4,于是
产能力(以每小时
解先核算过
2×1/100=0.80
0w=
1/4
根据式(3-58),达到最佳时,有
计算值大于题中所
0R=0+0w
数值,即A=20
40=0+0.80
0=22.2 min(或1332s)
再计算过滤
将θ及例3-6中给出的过滤常数、A代入恒压过滤方程式(3-44)中可求得滤液量
过滤压差为70k
V2+2×0.01×33×V=5×105×332×1332
根据式(3-42
V=8.2m3
相应的滤饼体积
VXc=8.2×0.08=0.66m3
滤布阻力一般不
滤框厚度=滤饼体积0.66
式为
A/2
33/2=0.04m
与洗水通道所改
第三章机械分离与固体流态化113
此即为最佳滤框厚度。
其生产能力可计算如下。操作周期=2×40=80min(或1.333h)
生产能力=0.66
1.333=0.5m3(滤饼)h-1
可见,最佳生产能力较例3-6的大。
(二)连续过滤机
1.操作周期
n,I min]
个
以转筒真空过滤机为例,一个操作周期就是旋转一周所经历的时间,设转筒的转速为每秒钟n次,则操作周期便为
o.-I
(3-60)
-3m3s
转筒真空过滤机在整个操作周期内只有部分面积进行过滤,也可以理解为:转筒的全部面积只在部分时间内进行过滤。设转筒表面浸入悬浮液中的分数为
,p=浸入角度
360
(3-61)
则过滤的部分面积就是A;部分时间就是/n。
2.生产能力
根据恒压过滤方程,略去滤布阻力,有V2=KA20,即转筒转一圈(一个操作周期)的滤液量为V=A√K0=A√K中/n,故转筒过滤机的生产能力为
Q--nV-AKm
(3-62)
式(3-62)表明,提高转筒的浸没分数中及转速n均可提高生产能力,但这类方法受到一定限制:若转速过大,则导致形成的滤饼过薄,不易从转筒表面取下;又若浸没分数提高,则洗涤、吸干、吹松等区域的分数便相应减小,可能达不到相应的要求。
长,没
【例3-8】例3-6中的悬浮液,拟改用转筒真空过滤机进行过滤。从产品样本中查得的有
能力。
关参数为:转筒直径2.6m,宽度2.6m,过滤面积20m2,转速范围为0.13~0.8r·min,浸
可知
入角度为90°~133°。生产中拟采用的转速为0.13r·min,浸入角度为130°。操作真空度为70kPa,若滤饼的压缩指数s=0.3,而且滤布阻力在压力改变时不起变化,试求生产能力(以每小时送出的滤饼体积表示)。
解先核算过滤面积
A=π×直径×宽度=π×2.6×2.6=21.2m2
计算值大于题中所列的数值(因未考虑筒周壁各段间的间隙)。过滤面积应采用题中所列数值,即A=20m2。
再计算过滤常数。例3-6中列出的过滤常数仅适用于过滤压差为0.3MPa的情况,现过滤压差为70kPa,故要进行修正。
根据式(3-42),K与△p成正比,故在本题条件下
1-0.3
K=5×10-5×()
=1.81×10-5m2.s-1
滤布阻力一般不因压力而变,故其相当的滤液量q亦不变,得本题条件下的过滤方程式为
q2+2×0.01q=1.81×10-50
(a)
极细的固体颗粒则关闭重液出
加以清除。
流态化是指固体颗粒层在
流态化了的颗粒表面能全部是
应;因而,流态化技术发展
却、干燥、吸附、煅烧和气
力消耗大,设备易磨损,颗
本节介绍流态化过程的
请阅读相关的资料。
图3-24有往复式卸料器的连续操作离心机
一、基本概念
1—转鼓;2—机壳;3—加料管口;4—加料斗;5—洗水管进口;
图3-25碟片式离心机
6一洗水喷头;7-往复推渣器;8一卸渣口;9一传动轮
1—加料;2一轻液出口;3一重液
如果流体自下而上地
出口;4一固体物积存区
(1)固定床阶段当
(3)碟片式离心机
此种离心机可用于分离不互溶的液体混合物,或从液体中分隙中流体的真实速度u1小
细的颗粒。如图3-25所示,机的底部做成圆固定床[见图3-27(a)]。
11
壳内有几十至一百以上的圆锥形碟片叠置成
一垂直轴带动而高速旋转。碟片在中央至周边刻
途上开有孔,各孔串联成垂直的通道。要分离的
体混合物从顶部的垂直管送入,直达底部,在
碟片上的孔上升的同时,分布于两碟片之间的
中,受离心力作用,密度大的液体趋向外周,
机壳内壁后上升到上方的重液出口流出;轻液则
(a)固定床
(b)流
向中心而自上方较靠近中央的轻液出口流出。
片的作用在于将液体分成许多薄层,缩短液滴
图3-27流态化
4
12
3
距离;液体在狭缝中流动所产生的剪应力亦有
破坏乳浊液。
(2)流化床阶段
2
若液体中含有少量细颗粒悬浮固体,这些
速度u稍大,此时床
亦趋向外周运动而到达机壳内壁附近沉积下来
着床层的膨胀,床内
间歇地加以清除。
减到沉降速度u3为止
碟片式离心机亦简称分离机,碟片直径可
时颗粒悬浮于流体中
图3-26管式超速离心机
1m,转速多在4000~7000 r•minl之间,分离
(3)颗粒输送阶
1一液体进口;2一制动器;3一重液;4一固体;为4000~10000。此种设备广泛用于润滑油脱水、度u3,则颗粒将被流
5一轻液;6一空气;7一转鼓(管);8一重液
出口;9一轻液出口;10一出口盖;
乳脱脂、饮料澄清、催化剂分离等。
依此,可以实现固体
11一带动机构;12一机架
(4)管式离心机在限定转鼓机械强度的
二、流化床的
下,提高转速,缩小转鼓直径,可以加大离心
根据颗粒在流
因数Kc。依此设计成的管式超速(高速)离心机,其直径一般为100~200m,高(一)散式流态
0.75~1.5 m,如图3-26所示。其转速约8000~50000 r·min, K达15000~60000,散式流态化现
液自底部的进口引人,在管内自下而上运行的过程中,因离心力作用,依密度同而分
流量逐渐增加时,
外两个同心层,到达顶部分别自轻液出口与重液出口送出管外。若用于从液体中分离出
加大,床层的上界
第三章机械分离与固体流态化115
较大的情况下,液面便可视为与转轴平行(见图3-22)。颗粒在被液体带动自下而上流动
的过程中,又受到离心力作用以一径向速度趋向鼓壁,其实际的轨线如图3-22中的虚线
所示。当悬浮液中某一颗粒沉降到达鼓内壁所需的时间,小于它从底部上升到转鼓顶部
所需的时间(即它在鼓内的停留时间),则此颗粒便能从液体中分离出来,否则将随液体
溢流而出。当颗粒层于鼓壁上达到一定厚度之后将其取出,清液则从鼓的上方开口溢流
而出。
(2)过滤式离心机鼓壁上开孔,覆以滤布,悬浮液注入其中随之旋转。液体受离心力
后穿过滤布及壁上的小孔排出,而固体颗粒则截留在滤布上。
(3)分离式离心机用于乳浊液的分离。非均相液体混合物被转鼓带动旋转时,密
度大的液体趋向器壁运动,密度小的趋向中央,分别从靠近外周的及近中央的溢流口
13流出。
浮液
离心机按结构分,主要有;转鼓式间歇离心机(以三足式离心机为代表)、转鼓式自动
3-71卸料连续离心机、碟片式离心机、管式离心机等。
其生
(1)三足式离心机图3-23所示为间歇操作的转鼓式离心机中最简单的一种。转鼓又称滤筐,是直立的,开口向上,从底部带动。机的外壳、转鼓和传动装置都悬在三个支柱上,故称三足式离心机。机盖打开后,浆料经加料管送入;机盖关闭后才能运转,从转鼓壁
机上的小孔甩出的液体集于机壳底部,用管子连续地引出。停止运转后机盖才能打开,滤渣从上方取出。也有转鼓底部可以开启,从下方卸料的设计。
3.图3-23三足式间歇操作离心机
1一转鼓;2一机壳;3一机盖;4一加料管;5一支柱;6一制动器把手;7一电动机
这种离心机转鼓的直径多在1m左右,转速为每分钟几百至一千多转,分离因数一般为600~1200。
(2)转鼓式自动卸料连续离心机图3-24所示为自动卸渣的连续操作离心机的一种。转鼓(滤筐)是平卧的,内衬金属网板,由水平轴带动旋转。浆料由加料管送到一个旋转的圆锥形漏斗中,此斗将滤浆加速之后送到滤筐内。沉积在筐壁上的固体物迅速脱水而成饼状。一个往复运动的推渣器将此固体渣向筐边缘推送30~50mm,然后往后退以空出新的过滤面来接纳新送到的滤浆。锥形加料斗与推渣器一起做往复运动。滤渣在被推到筐边缘落下之前,有喷头向其洒水进行洗涤。
此种形式的离心机的转速多在1000r•min1以内,适用于过滤颗粒直径较大(1mm左右)、浓度较大(30%以上)的滤浆,在食盐、硫酸铵、尿素等的生产中使用广泛。
114化工原理
浸没分数
130
360=0.361
过滤时间
0=.
中_
0.361166.6s
较大的情况下,液面便可视为与
=
n0.13
的过程中,又受到离心力作用以
将θ代入式(a),解得
60
所示。当悬浮液中某一颗粒沉降
转筒转一周得到的滤液量
q=0.0458m3·m-2
所需的时间(即它在鼓内的停留
V=qA=0.0458×20=0.916m3
溢流而出。当颗粒层于鼓壁上达
转筒转一周得到的滤饼量Ve=cV=0.08×0.916=0.0733m3
以每小时计的生产能力
而出。
(2)过滤式离心机鼓壁上
Q=60Ven=60×0.0733×0.13=0.572m3(滤饼)•h
后穿过滤布及壁上的小孔排出,
滤饼厚度为
L=
Ve0.0733
(3)分离式离心机用于
A20=0.00367m(或3.7mm)
度大的液体趋向器壁运动,密
显见,滤饼比较薄,但本题已采用了产品样本中对本设备规定的最小转速(0min'),不能再降低转速来增加过滤时间以提高饼厚。此计算结果表明,本题中的是
流出。
离心机按结构分,主要有
体颗粒含量低,采用转筒真空过滤机则滤饼过薄,不如采用板框压滤机合适。但与例卸料连续离心机、碟片式离心
(1)三足式离心机图3
较后,仍可看出:转筒真空过滤机在过滤推动力小得多、过滤面积也较小的条件下,能力(0.572 m3·hl)仍大于压滤机在最佳操作周期下的生产能力(0.50 m3h),
称滤筐,是直立的,开口向
上,故称三足式离心机。机
液中固含量多、颗粒粗(采矿、煤炭、无机盐化学工业中常见),则采用转筒真空过上的小孔甩出的液体集于机
效果远优于压滤机。
上方取出。也有转鼓底部可
第四节离心分离
利用离心力分离非均相混合物的过程称为离心分离。其设备除前述的旋风(液)分外,更重要的还有离心机。
离心机的主要部件是一个载着物料、高速旋转的转鼓。其产生的离心力,可将悬的固体微粒沉降或过滤而除去,或使乳浊液中两种密度不同的液体分离。
离心分离可以对一般沉降或过滤方法不能分离的混合物进行分离,其速率也较例如悬浮液用过滤方法处理若需1h,用离心分离只需几分钟,而且可以得到比较干的体渣。
离心机转鼓的直径或转速愈大,离心力愈大,对分离愈有利。这与旋风分离器直径
分离性能好的特点似乎有矛盾,其原因在于二者离心力产
方式不同:离心机是由设备本身的旋转产生离心力,其离
1一转鼓;
速度a,=r(2πn)2,可见,直径或转速愈大,a,愈大。后都
是由被分离的混合物以切线方向进入设备而产生离心力。
这种离心机转鼓的
线速度u1一定时,根据离心加速度a,rw2=u2/r可知,为600~1200。
h备直径愈小,则a,愈大,对分离愈有利。
(2)转鼓式自动
离心机按其所产生的离心力与重力之比,即离心分离转鼓(滤筐)是平卧
Kc=a,/g值的大小,有常速(Kc<3000)、高速(3000<K圆锥形漏斗中,此斗
50000)与超速(Kc>50000)之分。
状。一个往复运动的
离心机按分离的方式分,则有下列几种。
过滤面来接纳新送到
(1)沉降式离心机加料管将含固体微粒的悬浮液(下之前,有喷头向其
图3-22颗粒在离心常含颗粒很小且浓度不大)连续引到转鼓底部,使其在
此种形式的离
机内的沉降
自下而上流动。转鼓旋转时,液面形成抛物线形,但在右)、浓度较大(30
第三章机械分离与固体流态化117
极细的固体颗粒则关闭重液出口,只留轻液出口。附于管壁上的小颗粒,可间歇地将管取出加以清除。
第五节固体流态化
流态化是指固体颗粒层在流体的带动下,能使颗粒具有流体某些表观特性的过程。由于流态化了的颗粒表面能全部暴露于周围剧烈湍动的流体中,从而强化了传热、传质和化学反应;因而,流态化技术发展很快,许多工业部门在处理粉粒状物料的输送、混合、加热或冷却、干燥、吸附、煅烧和气-固反应等过程中,都广泛地应用了流态化技术。其缺点则是动力消耗大,设备易磨损,颗粒易碎。
本节介绍流态化过程的一些基本知识,至于流态化过程中的传热与传质问题的详细讨论
某片式离心机
请阅读相关的资料。
液出口;3一重液
一、基本概念
固体物积存区
如果流体自下而上地流过颗粒层,根据流速的大小,会出现下述三种不同情况。
从液体中分离
(1)固定床阶段当流体通过颗粒床层的表观速度(即空床速度)u较低时,颗粒空
底部做成圆锥隙中流体的真实速度u1小于颗粒的沉降速度u2,颗粒将保持静止状态,此时的颗粒层称为固定床[见图3-27(a)]。
片叠置成层,
中央至周边的
道。要分离的
达底部,在
谍片之间的
趋向外周,
流出;轻液
口流出。
(a)固定床
(b)流化床
(c)颗粒输送
缩短液滴沉具
图3-27流态化过程的几个阶段
图3-28聚式流化床
应力亦有助
(2)流化床阶段当流体的表观速度u加大到某一数值时,真实速度u比颗粒的沉降
体,这些颗速度u稍大,此时床层内较小的颗粒将松动或“浮起”,颗粒床层高度也有明显增大。但随
沉积下来,着床层的膨胀,床内空隙率e也增大,而真实速度u1=u/e,将随着的增大而减小,直至减到沉降速度u。为止。也就是说,在某一表观速度下,颗粒床层只会膨胀到一定程度,此
直径可达时颗粒悬浮于流体中,床层有一个明显的上界面,这种床层称为流化床[见图3-27(b)]。
,分离因数
(3)颗粒输送阶段如果继续提高流体的表观速度u,使真实速度u大于颗粒的沉降速
油脱水、牛度u,则颗粒将被流体所带走,此时床层上界面消失,达到了颗粒输送阶段[见图3-27(c)],依此,可以实现固体颗粒的气力输送或液力输送。
强度的条件
二、流化床的两种状态
大离心分离
根据颗粒在流体中分散得是否均匀,可将流态化分成散式流态化和聚式流态化。
m,高约为
(一)散式流态化
000。乳
散式流态化现象一般发生在液固系统。此种床层中颗粒能均匀地分散在流体中。当流体
而分成内流量逐渐增加时,床层从开始膨胀直到颗粒被带走,床内颗粒的分散状态和扰动程度平缓地
离出少量加大,床层的上界面较为清晰,如图3-27(b)所示。
118化工原理
(二)聚式流态化
聚式流态化现象一般发生于气固系统,这也是目前工业上应用较多的系统所示。其特点是床层中存在两个相:其一是颗粒浓度大、分布较均匀的乳化相(一是夹带少量颗粒、以气泡形式通过的气泡相(稀相)。当气泡到达床层顶部则处的颗粒溅散,使得床层上界面起伏不定,造成床层波动。当气量增大时,乳化相起流的空和气其余的气更大的气泡通式中,g、p、分别为流体和固体
将式(3-64)代人式(3-63)
开始,床层的波动逐渐加剧,但其膨胀程度却不大。
聚式流化床中可能发生以下两种不正常现象。
△
(1)腾涌如果床层高度与直径的比值大、气速又高时,气泡就容易相互聚即
泡,当气泡直径大到与床径相等时,就将床层分隔成几段,床内颗粒群以活塞推进的
再对图3-30中截面1-1与
上运动,在达到上部后气泡破裂,颗粒又重新回落,这即是腾涌,亦称节涌。腾涌间的接触状况恶化,加剧颗粒的磨损与带出,并使床层受到冲击、发生震动,甚至式中,△p为压力损失。
构件。
结合上式与式(3-65),得
(2)沟流在大直径床层中,由于颗粒堆积不匀或气体初始分布不良,可在床方形成沟流。此时,大量气体经过局部地区的通道上升,而床层的其余部分仍处于固
上式表明,在流态化阶段
态(死床)。显然,当发生沟流现象时,气体不能与全部颗粒良好接触,将使工艺过全部颗粒的净重力。由于后
恶化。
化,故流化床的压力损失△p
三、流化床的主要特性
中水平线段BC所示。注意
上倾斜是由于流体流过器壁
(一)类似液体的特性
增大而造成的。
流化床在一些方面呈现出类似液体的性质。例如,当容器倾斜时,床层上表面将
图中AB段为固定床阶
平[见图3-29(a)];将两床层相通,它们的床面将自行调节至同一水平面[见图3-290阶段流速较低,颗粒较细时
床层中任意两点压力差可以用液柱压差计测量[见图3-29(c)];流化床层也类似液体期压力损失与表观速度的一次
动性,如容器壁面开孔,颗粒将从孔口喷出,并可像液体一样由一个容器流人另一段为斜率等于1的直线。图
[见图3-29(d)],这一性质使流化床在操作中能够实现固体的连续加料和卸料
化床回复到固定床时的压力
于颗粒从逐渐减慢的上升气
也小一些,故AB段处在
A
CD段向下倾斜,表示
P
平衡颗粒重力所需的压力自
2
根据流化床恒定压力
层流化的优劣。如果床内出
损失较正常时为低。
(a)
(b)
1
(c)
四、流化床的操作流
图3-29流化床类似于液体的特性(d)
流化床的空隙率随流
(二)几乎恒定的压力损失
图3-30流化床
可以有一个较宽的范围。
床层一旦流化,全部颗粒处于悬浮状态,则整个床层受力平衡,即合力为零。现取
床层开始流态化时的
床层做受力分析,如图3-30所示。忽略流体与容器壁面间的摩擦力,则整个床层的被带出时的流体表观速度
(包括流体)等于床层的压差△p(△P=P1-P2)乘以截面积A,即
小于u
(一)起始流化速度
式中,m为床层中颗粒的总质量,kg;m1为床层内流体的质量,kg
△pA=mpg+m1g
(3
令床层高度为L,则
起始流化速度又称临
图3-31中的点B所示,
验测定,也可用下述方法
mg-(AL-)pg
(3
当颗粒较细时,流体
液通过滤渣导出的式(3-3
统,如图
目(密相)
第三章机械分离与固体流态化119
则破裂而将式中,p、p。分别为流体和固体颗粒的密度,kg·m3
化相仍基本
将式(3-64)代入式(3-63),得
从起始流态
△pA-mp(p-p)g+ALPg
s
即
△p-Log=mp(p2-p)g
Ap.
(3-65)
聚合成大
再对图3-30中截面1-1与2-2间的流化床做机械能衡算有
进的方式
△p=Lpg+△p
式中,△pt为压力损失。
涌使气固
结合上式与式(3-65),得
至损坏
△pr=△p-Lpg=
e(ps-p)8
Aps
(3-66)
末内局
上式表明,在流态化阶段,流体通过床层的压力损失等于流化床中以单位床层面积计的
干固定市全部颗粒的净重力。由于后者不随流速而变
过程化,故流化床的压力损失△P不变,如图3-31
固定床
流化床
带出开始
中水平线段BC所示。注意,图中BC段略向
B
上倾斜是由于流体流过器壁的阻力损失随气速a
增大而造成的。
D
A
图中AB段为固定床阶段,由于流体在此
A
将保持阶段流速较低,颗粒较细时常处于层流状态,
起始流化速度
带出速度
29(b)]压力损失与表观速度的一次方成正比,因此该
lgu
本具有段为斜率等于1的直线。图中A′B段表示从流
图3-31流化床压力损失与气速关系
个容化床回复到固定床时的压力损失变化关系,由
于颗粒从逐渐减慢的上升气流中落下所形成的床层较随机装填的要疏松一些,导致压力损失也小一些,故AB段处在AB段的下方。
CD段向下倾斜,表示此时由于某些细颗粒开始为上升气流所带走,床内颗粒量减少,平衡颗粒重力所需的压力自然随着下降,直至达到某一气速颗粒全部被带走。
根据流化床恒定压力损失的特点,在流化床操作时可以通过测量床层压力损失来判断床层流化的优劣。如果床内出现腾涌,压力损失将有大幅度的波动;若床内发生沟流,则压力损失较正常时为低。
四、流化床的操作流速范围
流化床的空隙率随流体表观速度的增大而变大,因此,能够维持流化床状态的表观速度可以有一个较宽的范围。
床层开始流态化时的流体表观速度称为起始流化速度,用u表示。当某指定颗粒开始被带出时的流体表观速度称为带出速度,用u表示。流化床的操作流速应大于u,又要
整小于uo。
量
(一)起始流化速度umf
起始流化速度又称临界流化速度,或最小流化速度,它是固定床到流化床的转折点,如图3-31中的点B所示,故可通过固定床与流化床压力损失线的交点决定。此交点最好由实验测定,也可用下述方法估算。
当颗粒较细时,流体通过固定床层的空隙为层流,其压力损失△P可应用第三节对滤液通过滤渣导出的式(3-35)
原理
3-11一转简真空过滤机的过滤面积为3m2,浸没在悬浮液中的部分占30%。转速为0.5r*min关的数据如下。
滤渣体积与滤液体积之比c=0.23m2m3,过滤常数K=3.1×10‘m2•s1,滤液黏度p1
符号鼓内的绝压为30 kPa.大气压为101.3 kPa(绝),滤布阻力可以忽略。试计算:(1)-每小时积;(2)所得滤渣层的厚度,
A
意义
符号说明
a
面积
a
质量分率
单位
m2
符号意义
a
比表面积
qe
通过单位面积滤布的当单位
液体的搅拌是化学
B
离心加速度
m-1
量滤液体积
种或多种可互溶的液体
宽度
ms-2
半径
年年如用与液体不互溶的溶
滤饼体积与滤液体积之比
比阻
m
m
在液体中悬浮,例如在
D
s
滤饼的压缩指数
m2
的可溶物质,用固体吸
d,dp
直径(设备)
m3·m-3
u
m
在液体反应物中等;使
dAm
直径,颗粒直径
流速,过滤速度,表观流速
uo
m
沉降速度,带出速度
容器壁之间的传热,以
dLm
表面积平均直径
ui
进口速度
ms
长度平均直径
m
dvm
u
在固定床或滤饼孔隙中myl
体积平均直径
m
dvAm
ms
de
体积表面积平均直径
m
流动的真实速度
umi
m
起始流化速度
一、主要部件
H
旋风分离器的颗粒临界直径
ur
ms
m
径向速度
常用的机械搅拌
高度
J
u
ms
m
切线速度
①
盛装被搅拌液
洗涤液体积与滤液体积之比
K
体积
ms
②一根旋转的轴
过滤常数
V
m3
K0,K1
m2s-1
过滤介质的当量滤液体积
③辅助部件,如
比例常数
V
L
体积流量
m3
图4-1所示为生
长度,滤饼厚度,流化床高度
ms
Le
过滤介质的当量滤饼厚度
m
洗涤速率与最终过滤
它随轴旋转而将机械
Iemf
起始流化床高度
m
速率之比
出,搅拌装置的性能
le
长度
m
床层空隙率
叶轮的形状、大小和
m
Emf
m
质量
起始流化床空隙率
搅拌槽的形状和大小
效率
mp
固体床层质量
kg
0
二、叶轮形式
N
kg
时间
气体通过旋风分离器时的旋转圈数
s
叶轮的式样很多
μ
黏度
n
颗粒数
5
Pas
上有三类:桨式、透
n
转速
阻力系数
密度
(1)桨式叶轮
压力
s1
kgm
9
通过单位面积的滤液体积
Pa
Ps
颗粒密度
上的平板构成的平桨
kgm
m3·m-2
转筒过滤机浸没分数
叶片有时是斜的,但
球形度
央以低速或中速旋转
槽壁运动,然后再向
1金绿松等,离心分离,北京;化学工业出版社,2008
参考文献
动。若槽比较深,则
2吴占松等.流态化技术基础及应用,北京:化学工业出版社,2006
桨。平桨式搅拌器可
化、气体的分散。此
理高黏度的液体。它
使固体悬浮的效果较
单桨式叶轮的总
为20~150r•min1,
速很低时,桨式叶轮
液体便沿槽壁打漩而
第三章机械分离与固体流态化121
umi=-
d2v(p3-p)g(0.3×10-3)2×(1150-0.48)×9.81
1650p
auter)
1650×3.53×105
0.0174 ms-
核算RemfRem
=0.3×10-3×0.0174×0.48
3.53×10-5
=0.071(<20)
故对um的计算有效。
将p=0.48kg·m3、μ=3.53×10-5Pa·s代人式(3-21)得
Em及
d2(p3-p)g_(0.15×10-3)2×(1150-0.48)×9.81-0.40ms-1
=181
18×3.53×10-5
核算ReoReo=duop0.15×10-3×0.40×0.48
μ
3.53×10-5
=0.82(<2)
故对u0的计算有效。
(3-6
A-Ell方于是
uo0.40
umf0.0174=23
25.
(3
习
题
发现
3-1求直径为 60μm的石英颗粒(密度 2600 kg·m3)分别在20℃水中和20℃空气中的沉降速度。
3-2一种测定液体黏度的仪器由一钢球及玻璃筒组成,测试时筒内充有被测液体,记录钢球下落一定距离所需的时间即可测出液体黏度。已知球的直径为6mm,下落距离为200mm所需的时间为7.32s,此糖浆的密度为1300 kg·m3,钢的密度为7900kg·m3。求此糖浆的黏度。
3-3
(3-6
某降尘室长2m、宽1.5m、高2m。在常压、100℃下处理2700m3·h的含尘气体,气体的物性与空气相同。设尘粒为球形,其密度为2400kg·m3,试求:(1)能被完全除去的最小颗粒直径;(2)
0。
直径为50μm的颗粒有百分之几能被除去?
3-4速溶咖啡粉(密度为1050kg·m3)的直径为60μm,被250℃的热空气带入旋风分离器中,进入时的切线速度为20m·s。在分离器内的平均旋转半径为0.5m,求其径向沉降速度及分离因数。
降
3-5某淀粉厂的气流干燥器每小时送出10000m3带有淀粉颗粒(密度为1500kg·m3)的80℃热空气。
应当
为了从中分离出淀粉颗粒,采用图3-7所示的旋风分离器。器身直径D=1000mm,其他部分的尺寸按图中所列的比例确定。取气体旋转圈数为5,试估计理论上的临界粒径d;计算直径为10μm的颗粒的理论粒级效率,并利用图3-8估算其实际粒级效率。若阻力系数取8,则设备的阻力损失为多少kPa?
球
3-6原用一个旋风分离器分离排放气中的灰尘,因分离效率不够高,拟改用三个同一型号、较小规格的并联,其各部分尺寸的比例不变,气体进口速度也不变。求每个小旋风分离器的直径应为原来的百分之多少?可分离的临界粒径为原来的几倍?
3-7在实验室内用一片过滤面积为0.05m2的滤叶在36 kPa(绝)下进行吸滤(滤浆压力保持为1个大气压)。在300 s内共吸出400cm3滤液,再过600 s,又吸出400cm3滤液。试估算:(1)该真空过滤的过滤常数K、q;(2)再收集400cm3滤液所需的时间(3)若每收集1L滤液有5g固体物沉积在滤叶上,求比阻r(m·kg1)。滤液黏度为1 mPa·s,滤渣不可压缩。
3-8
某板框压滤机在恒压过滤1h之后,共送出滤液11m3,停止过滤后用3m3清水(其黏度与滤液相同)于同样压力下对滤饼进行洗涤。求洗涤时间,设滤布阻力可以忽略。
v-kAe.
3-9用板框压滤机过滤某悬浮液,框的长、宽均为450m,共有10个框。过滤压力为400kPa,不洗涤,滤布阻力可以忽略。此外,拆卸、重装等辅助时间共为1200s。试求其最大生产能力(m3滤液·hl)。已测得过滤常数K=4.3×10-7m2·s-1。
B
3-10,有一转筒真空过滤机,每分钟转2周,每小时可得滤液4m3。现要求每小时获得5m3滤液,试求:(1)其转速;(2)转筒表面滤渣厚度为原来的几倍?滤布阻力可以忽略不计。
将式中的比表面积a用式(3-3),即a=6/dv表示。得到
E
AP
2Koa2(1-e)2μL
式中,dey为非球形颗粒的体积当量直径,对于非均匀颗粒群,应采用部特(Saute
m;φ为球形度。
△P1=72K。
dv(
(1-e)2uuL
1
E(odev)?
devu
根据欧根(Ergun)的实验数据,层流时72K。取为150,代入上式得
核算Re
mf
故对um的计算有效。
当 u达到起始流化速度 um时, △p、e及L都达到固定床的最大值 △Pmt、 Eth
△p1=150(1-e)2uuL
将p=0.48kg·m
d2(p
式(3-67)改写为
E3(odev)2
t=duop
核算ReReo=
△pmf=150(1-Em)2umiμLmi
的计算有效。
将式(3-67a)与流化床压力损失计算式[式(3-66)]联立,并利用mp=ALmt(1-
(odev)2
故对ug
这一关系,可得起始流化速度
于是
umf(dev)2(p-p)g t
t
150u
1-Emf
应用上式计算 umi时,em和φ的可靠数据常难以获得。而对于常见的细颗粒,3-1求直径为60μm的
1一m~11,代式(3-68)得
一种测定液体黏度
Emi
3-2所需的时间即可测
糖浆的密度为1300
dev(ps-p)g
umf
3-3某降尘室长2m、
1650μ
式(3-69)适用于起始流化雷诺数 Remi=dev umio/μ约小于20的范围,偏差约达士30%
3
空气相同。设尘粒
直径为50μm的颗
(二)带出速度
3-4速溶咖啡粉(密度
颗粒床层通常由非均匀的颗粒组成,当流体表观速度u稍大于某指定粒径颗粒的
的切线速度为20
度u。时,此种颗粒及更小的颗粒将被流体带出,故流化床中指定粒径颗粒的带出速度
3-5某淀粉厂的气流干
等于其沉降速度u。层流范围内,u。按式(3-21)计算
为了从中分离出
按图中所列的比例
粒的理论粒级效
uo=d2(ps-p)g
18μ
少kPa?
流化床操作流速范围的大小可用um/u表示。设想一理想情况:床层由直径相同
3-6原用一个旋风分
形颗粒组成,则式(3-69)中的dy与式(3-21)中的d相等,在两式都适用的范围内
联,其各部分尺
uo1650
多少?可分离的
3-7
umf
18=91.7
在实验室内用
可见,流化床的操作流速范围可以相当宽。实际上,由于床内颗粒通常大小不均匀,
压)。在300s内
的颗粒粒径d<dy,使得操作流速范围比上述的要窄。若颗粒较大,流化或带出时超
的过滤常数K、
流范围,式(3-69)及式(3-21)不适用,其适用公式算出的u/um(也要比上述的小。
在滤叶上,求比
3-8
【例3-9】流化床反应器所用的硅胶催化剂颗粒的平均直径dy=0.3 mm,密度A
某板框压滤机
同)于同样压
1150 kg·m3,求其在470℃气流中的起始流化速度u。设气体的物性可近似按空3-9用板框压滤机
算。又若不希望粒径d=0.15 mm的催化剂被带出,气速范围u/umi为多少?
滤布阻力可以
解根据附录六可得 470 ℃千空气的 p=0.48 kg•m3、 μ=3. 53×10-5 Pa+s,
已测得过滤常
式(3-69)
3-10,有一转筒真空
(1)其转速;
min
黏度p=1mP
(1),每小时的
第四章搅
单位
拌
*M
液体的搅拌是化学工业中经常使用的一种单元操作。借搅拌以达到的目标通常是:使两
m
种或多种可互溶的液体彼此混合均匀,例如用溶剂将浓溶液稀释;使不互溶的液体混合,例
m2
如用与液体不互溶的溶剂对前者进行洗涤;用液体萃取另一液体,或制备乳浊液等;使固体
在液体中悬浮,例如在液体中溶化固体颗粒,从溶液中将固体结晶出来,用液体浸取固体中
速mesl
的可溶物质,用固体吸附液体中的污染物,促进液体与固体之间的化学反应,将催化剂悬浮
在液体反应物中等;使气泡较密切地与液体接触,以加快气液间的传质或反应;促进液体与
m
容器壁之间的传热,以防止局部过热等。
ms1
第一节搅拌设备
ms
一、主要部件
ms1
常用的机械搅拌装置由下列部分组成:
ms-1
①盛装被搅拌液体的容器,称为搅拌槽;
m3
②一根旋转的轴及安装在轴上的推动器(或称叶轮);
m?
③辅助部件,如支架、密封装置、槽壁上的挡板等。
n3s-1
图4-1所示为生产中用的一个典型的搅拌装置。搅拌系统的主件是叶轮(或称推动器),它随轴旋转而将机械能施加于液体,推动液体运动。但应指
出,搅拌装置的性能如何,它消耗的功率多少,不仅取决于
叶轮的形状、大小和转速,也取决于所搅拌液体的物性以及
0
搅拌槽的形状和大小、槽壁上有无挡板等因素。
二、叶轮形式
叶轮的式样很多,但除特殊情况以外,广泛使用的基本
9
上有三类:桨式、透平式和船用螺旋桨(简称螺旋桨)式。
3-
8
(1)桨式叶轮对于简单的搅拌问题,用安装在垂直轴4
0
上的平板构成的平桨即可,常用的有两片桨叶或四片桨叶。
5
7
-3
叶片有时是斜的,但较普通的还是垂直的。垂直叶片在槽中
央以低速或中速旋转,将液体沿径向及切向拨动;液体先向
槽壁运动,然后再向上或向下流。若用斜片桨,还有轴向推
动。若槽比较深,则一根垂直轴上可以自上而下安装几组
图4-1典型的搅拌器装置
桨。平桨式搅拌器可用于简单的液体混合、固体的悬浮和溶1一电动机;2一减速器;3一插入管;
化、气体的分散。此种叶轮并不产生高速液流,故适用于处
4一夹套;5一挡板;6一排放阀;
理高黏度的液体。它的主要缺点是不易产生垂直液流,因此
7一搅拌桨;8一温度计套;
9一液面
使固体悬浮的效果较差。
单桨式叶轮的总长一般为槽内径的0.5~0.8倍,桨叶的宽度为其长度的1/16~1/10,转速为20~150 r•minl,搅拌桨末梢速度(外端的圆周速度)小于3 m•sl,一般是1.5~2 m•sl。转速很低时,桨式叶轮在不加挡板的槽内可造成平缓的搅拌;若转速较高,槽壁上要装挡板,否则液体便沿槽壁打漩而少混合作用。
有一种特制的桨其轮廓与槽的内壁十分密合,旋转时与槽壁形成的缝隙很小
奖叶(见图4-2)。它的特点是其刮扫作用可以防止搅拌桨与槽壁之间产生一层静
去壁上的沉积物,从而有利于传热,但它所起的混合作用是很弱的。
(2)透平式叶轮如图4-3所示。它与叶片数目多而长度短的桨式叶轮相似,大。这是化工厂中使用最广泛的搅拌器,能有效地完成几乎所有的搅拌方式并能处理
围较广的液体。它们在产生径向液流时特别有效,但亦同时引起轴向液流,尤其在
挡板时。对混合液密度相差不大的液体,它们的效力极为显著。此外,其造价也比体随叶轮团团转的运动:
形式的搅拌器低。
的对称,螺旋桨式叶轮通
打漩现象消除后,槽
有挡板的搅拌槽中搅拌
轮轴垂直,并在槽壁和
直的液流,亦有横向的液
叶轮若是螺旋桨式,则
示。与透平式或桨式叶
液体混合。
挡
图4-2锚式桨叶
(a)侧视图
图4-3透平式叶轮
图4-4螺旋桨式推动
图4-5
最普通的叶轮有6个平片安装在一个中心圆盘上(见图4-3),亦有采用弯片而不用的,这样可以降低功率消耗。叶轮亦可做成闭式,即于上、下两侧加盖板,与离心泵
液体混合系统的搅
叶轮相似。此种叶轮的直径比平桨式的小,是槽径的0.3~0.5倍。
(3)螺旋桨式叶轮这是一种高速旋转、引起轴向流动的搅拌器件。标准的螺旋桨式式中,u1为末梢速度
三瓣叶片,叶片的螺距与螺旋桨的直径相等,如图4-4所示。叶轮旋转的速度约为1500rm
透平式叶轮的末
可与电动机的全速相同,直径较大者转速亦可达400~800r·min1。末梢速度可达14~16m这类搅拌器是轴向流动式,产生强烈的湍动,而且螺旋桨叶强烈地剪切液体。由于液流能持
搅
能渗及远方,因此对搅拌低黏度的大量液体有良好效果,但不适用于高黏度液体。
低
螺旋桨式推动器即使安装在很大的槽内,其直径亦不超过45cm。槽比较深时亦
中
两个或更多的推动器。
高
三、叶轮的操作
四、搅拌槽与挡
叶轮旋转时,推动一股液体使它流动,要收到良好的搅拌效果,离开叶轮的液体
搅拌槽一般是直
须足够大,能推进到搅拌槽中深远之处。这股液体具有一定的动能,当其在其余的液体
为简单计亦可用平底
过时,其动能由于液体的内摩擦而耗散,变为热能,可使被搅拌的液体温度稍升高
宜采用。方形槽或
如果搅拌槽是平底圆形槽,槽壁光滑并没有安装任何障碍物,液体黏度不大,而且
槽壁上若安装
放在槽的中心线上,则液体将随着叶轮旋转的方向循着槽壁滑动。这种旋转运动产生所或1/12,其长度一
打漩现象,可造成下列不良后果:液体只是随着叶轮团团转,而很少产生横向的或垂
可离开槽壁放置(
下运动及发生混合的机会;叶轮轴周围的液面下降,形成一个旋涡,旋转速度愈大则旋洲
度液体用的挡板应
心向下凹的程度愈深,最后可凹到与叶轮接触。此时,外面的空气可进入叶轮而被吸到
透平式或螺旋桨式
中,叶轮所接触的是密度较小的气液混合物,所需的搅拌功率显著下降,这却表明打
了挡板的作用。
还限制了施加于液体的搅拌功率并限制了叶轮的搅拌效力;打时功率的波动会引起异五、典型搅拌
作用力,易使转轴受损。避免打漩现象的方法有:在搅拌槽壁上安装垂直挡板,借以打图4-7所示为
称为
静止膜小
第四章搅拌125
,但其和体随叶轮团团转的运动;或不将叶轮放在槽的中心线上而放在偏心的位置上,借以破坏系统
处理黏度的对称,螺旋桨式叶轮通常采用此法而不需挡板。
在槽壁上
打漩现象消除后,槽内液体的流型即取决于叶轮的形式。透平式或桨式叶轮在壁上
有挡板的搅拌槽中搅拌黏度不高的液体时,产生径向流型。径向流动主要与槽壁和叶
多数其轮轴垂直,并在槽壁和叶轮轴附近转折而向上下垂直流动,如图4-5所示。此时既有垂
直的液流,亦有横向的液流,使液体有良好的从顶到底的翻转运动,从而有利于混合。
叶轮若是螺旋桨式,则产生轴向流型。轴向流动主要与槽壁和转轴平行,如图4-6所
示。与透平式或桨式叶轮的情形一样,也有垂直液流和横向液流,因此也产生良好的
液体混合。
挡板
挡板
(a)侧视图
(b)底视图
(a)侧视图
(b)底视图
推动器
图4-5径向流型
图4-6轴向流型
用平
液体混合系统的搅拌程度通常用叶轮叶片的末梢速度u1来衡量。其计算式如下。
的团
ut=πDn
(4-1)
式中,u为末梢速度,m·sl;D为叶轮直径(或叶片总长),m;n为叶轮转速,sl
透平式叶轮的末梢速度范围见表4-1。
叶轮
min
表4-1透平式叶轮的末梢速度范围ut/ms-1
n's!
搅拌强度
久目
低度搅拌
2.5~3.3
中度搅拌
3.3~4.1
高度搅拌
4.1~5.6
安装
四、搅拌槽与挡板
搅拌槽一般是直立的圆筒形槽。槽底的构型以有利于流线型流动为宜,故多为碟形底,
度必
为简单计亦可用平底。锥形底因易形成停滞区及易使悬浮着的固体沉聚,除有特殊原因外不
口流
宜采用。方形槽或有棱角的槽因在有角之处的液体流动不畅,亦不宜采用。
槽壁上若安装挡板,一般用4个(多于此数没有必要)。挡板的宽度通常是槽径的1/10
轮
或1/12,其长度一般要使下端通到槽底,上端露出液面之上。对于中等黏度的液体,挡板
的
可离开槽壁放置(与壁相距一个挡板宽度),以防在槽壁与挡板接触之处形成停滞区。高黏度液体用的挡板应倾斜放置,并将宽度减小到槽径的1/20。液体黏度大于20000cP时,用透平式或螺旋桨式叶轮可不加挡板,因为高黏度对液体流动的天然阻力抑制打漩而自身起到了挡板的作用。
五、典型搅拌器构型
图4-7所示为一种所谓典型搅拌器的构型,这种构型对化工生产中多数工艺过程的液体
128化工原理
或
式中,Po(=N/pn3D5)为功率特征数;Re(=D2np/μ)为搅拌雷诺数;Fr(=n2Dg)弗劳德数;常数K为代表系统几何构型的总形状因数。
Po=KReFr
若把各种形状因数S1,S2,…,S也考虑进去,式(4-6)可写成
如果这些形状因数保持不变(即对某种构型的搅拌系统,其各部分尺寸的比例
Po=K'ReFrS{ S…S
式(4-6a)便简化为式(4-6)。以下解释所得三个搅拌特征数的含义。
搅拌雷诺数 Re=D2no/μ。第一章第三节已说明雷诺数代表加速力A=pd2u2与M=udu之比。在搅拌系统中,加速力A是叶轮或桨叶推动液体运动的力,其中,代度采用叶轮直径D,代表性速度采用叶轮外端速度 ut=πDnc Dn;于是AccpDcp(Dn)2=pD4n2。黏性力M是液体内的剪切力,是阻碍液体运动的力,M∞μDut=故有
ReccA/MccpD4n2/μD2n=pD2n/u
搅拌弗劳德数 Fr=n2D/g代表加速力A与重力G=mgpD3g之比
FrccA/GccpD4n2/pD3g=Dn2/g
以前(曲线的BC段)
搅拌功率特征数Po=N/pn3D5。由式(4-3)Ncpn3D5可知,Po即代表式中的比数。从另一角度看,功率N是推动液体的加速力与速度之积,
段),有足够的能量传
即
雷诺数,直到Re=10
Ncc Fut cpD2 u ut cpD2(Dn)3= on3D5
中的K和x并不恒定
与式(4-3)结果相同。
当流动变为充分
前述的式(4-6)又可写成
此时流动与雷诺数和
9=Po/Fry=KRex
式中,φ为功率函数。
所以对于有挡板的典
对于不打漩的系统,重力的影响甚微,可不考虑,弗劳德数的指数y可取为零,式(4-7)又简化为
在无挡板的搅
=Po=KRer
图4-9所示为与典型
二、功率曲线
(4
由图4-8与图
将中值对Re值在双对数坐标纸上标绘,可以得到所称的功率曲线。对于一个具体的
Re≈300(各曲线的
何构型,只有一条功率曲线,它与搅拌槽的大小无关。因此,大小不同的搅拌槽,只要
数曲线陡然下降,
构型相似(各部分的尺寸比例相同),就可以应用同一条功率曲线。
中的指数x为一变
文献上已发表了许多不同的功率曲线,它们代表许多不同几何构型的搅拌器。利用
斜率为负而趋于成
曲线根据Re读出后,即可求出Po以及功率N。
图4-8所示为前述有挡板典型搅拌器(见图4-7)的功率曲线。由图4-8可知,在低
诺数(Re<10)下,功率曲线是一段斜率等于-1的直线。在此区域(线段AB)中,
的黏性力控制着系统内的流动,而重力的影响可忽略,因此可不考虑弗劳德数。此层流区
内的直线AB可用下式表示
中=Po=N
on3D5=71.0Re-1.0
(49
即
N=71.0(on3D5)
所以对于有挡板的典型构型搅拌器,Re<10时
(o
N=71.0μn2D3
(4-10)
当雷诺数增加时,流动从层流过渡到湍流。对于典型构型,这种过渡缓慢。在Re≈30
尺寸为
装在
第四章搅拌127
T;
拌过程都完全可以用前述三种形式的搅拌器完成。问题在于了解有关的工艺过程对搅拌器中的液体流型、液体循环流量和剪切力大小这几方面的要求以及这三种搅拌器可采用的具体构型,从而确定出叶轮尺寸和转速大小的合理配合,以产生所要求的流量和剪切力,并估算出其功率消耗,而不在于另外设计式样新奇的设备。
第二节
搅拌功率
并从被
搅拌器的功率是为了达到规定的搅拌目的而需付出的代价,是衡量其性能好坏的根据之一,
液体受搅拌所需功率取决于所期望的液流速度及湍动的大小。具体地说,功率与叶轮形
为了状、大小和转速,液体黏度和密度,搅拌槽的大小和内部构件(有无挡板或其他障碍物)以
它并及叶轮在液体中的位置等有关。由于所涉及的变量多,进行实验时可借助于量纲分析,将功
或率消耗和其他参数联系起来。
若液
一、功率关联式
用多
经验表明,搅拌器在槽中搅拌液体的功率消耗取决于下列变量:叶轮直径D和转速n,液体密度p和黏度μ,重力加速度g;以及槽径T,槽中液体深度H1,挡板数目、大小和位置等几何尺寸。假定这些尺寸都和叶轮直径成一定的比例(例如符合对典型搅拌器构型的规定),并将这些比值定为形状因数,如S1=T/D、S2=w/D、S3=r/D等(见图4-7)。考虑
量重力影响的原因是:除非完全消除了打漩现象,否则液面上会出现旋涡,有一些液体被升举到平均液面以上,而这种升举需克服重力。
(4
暂不考虑形状因数,则功率N可表述为上述变量的函数
N=f(n,D,p,μ,g)
(4-5a)
3
用第一章介绍过的量纲分析法,设N=KnaDbpμdge
(4-5b)
小是
式中,K为无量纲常数。
以质量(M)、长度(L)、时间(T)为基本量纲,可将式(4-5b)转换为下述量纲关
瓦量贝
系式
ML2T-3=(T-1)(L)6(ML-3)c(ML-1T-1)d(LT-2)
43
即
ML2T-3=Mc+dLb-3c-d+eT-a-d-2e
一定
比较等号两侧各量纲的指数,得下列关系
c+d=1
b-3c-d+e=2
-4
-a-d-2e=-3
大
可解得
剪
c=1-d,b=5-2d-e,a=3-d-2e
要
代人式(4-5b),得
速
N=Kn3-d-2eD5-2d-epl-dudge
可
上式可改写成
N-K(D)(D)
(4-5c)
pn3 Ds
令:x=—d,y=—e,则式(4-5c)又可写成
-()()
(4-5)
原理
Wb挡板
转轴
槽
混合要求能够满足。典型搅拌器的几何
①叶轮为透平式,有6个平片,安
为s的中心圆片上;
拌过程都完全可以用前述
②叶轮直径D=(1/3)搅拌槽直径的液体流型、液体循环流量
③叶轮距槽底的高度H;=1.0D
型,从而确定出叶轮尺寸和
④叶片宽度(高度)w=D/5;
其功率消耗,而不在于另外
6平片的
透平式叶轮
HL
⑤叶片长度r=D/4;
⑥液体深度H1=1.0T;
⑦挡板数目=4,垂直安装在槽壁上并
搅拌器的功率是为了
延伸到液面之上;
H1
⑧挡板宽度Wb=T/10。
之一
液体受搅拌所需功率
应该强调的是,上述典型构型只是状、大小和转速,液体黏
T
验研究有所根据而规定的,在某些场合及叶轮在液体中的位置等
图4-7典型搅拌器的构型
最适用的构型。例如,对于固含量很高率消耗和其他参数联系走
很高的液体,它可能就不适用。又如,
一、功率关联式
深度有所改变,可能要求叶轮靠近槽底;若深度大于槽径的1.25倍,则应使用
经验表明,搅拌器在
叶轮。
液体密度p和黏度μ,重
六、搅拌器的液体循环量与压头
置等几何尺寸。假定这些
叶轮旋转时,其作用与离心泵叶轮相仿,既输送液体又产生压头(施加给单位重量定),并将这些比值定为
的功),为此要消耗功率。体积流量、压头与功率之间的关系为
重力影响的原因是:除
到平均液面以上,而这
N=QHpg
(4
暂不考虑形状因数
式中,N为功率,W;Q为体积流量,m3·sl;H为压头,m;p为液体密度,kg·m
为重力加速度,m·s-2。
用第一章介绍过的量纲
压头H通常可以写成速度头u2/2g的倍数(u为液体的线速度,m·sl),速度头大
切力大小、也是湍动强弱的量度。叶轮外端速度u:可作为线速度的代表,而unD(D
式中,K为无量纲常数
轮直径,m;n为转数,sl),这样,叶轮所产生的液体速度头就与n2D2成正比。体积流
以质量(M)、长
与速度和面积之积[(nD)(D2)=nD3]成正比。将这两个关系式代人式(4-2),得
系式
ML
Nocon3 D5
(4
既然QcnD3,HcnD2,Nocn3D5,则Q/HcD/nccD8/3/N1/3。在功率消耗为-
即
值的条件下,下列关系成立
比较等号两侧各量纲
QCD
H
(4
从上述可得出一条关于叶轮操作的基本原则:在同等功率消耗下,一个旋转速度慢的
产的体量一个的小的体
可解得
切力大。换言之,对于产生高剪切力的搅拌器,希望其压头H大而体积流量Q小,
代人式(4-5b),得
度要高,而Q/H比值要小。反之,若希望有充分的混合但液体的剪切力不需要很高,
增加搅拌器的直径并减低其速度,以便获得的Q/H比值大。液体的混合,固体在液体中上式可改写成
悬浮或溶解,以及液-液萃取等操作要求高体积流量甚于高度湍动;气-液反应和某些液
触的搅拌则要求高度湍动甚于高体积流量。
值得指出:以往对液体搅拌这一过程的研究不充分,以至于在化工工艺过程中出现很令:x=-d,y=
拌器设计式样,其实并无必要。现已发现,除了极个别的情况以外,绝大多数普通液
n2D|g)为
第四章搅拌129
层流区
过渡区
+湍流区
比例固定
(4-
102
22与黏性
A
,代表性长
10
B
at=uDn
C
D
E
10
102103
104
Re=D2np/μ-
105
图4-8典型搅拌器构型的功率函数曲线(有挡板)
的比例常
以前(曲线的BC段),功率和流动特征仍只取决于雷诺数。在Re≈300以后(曲线CD段),有足够的能量传给液体引起打漩现象,但由于挡板有效地加以抑制,故流动仍取决于雷诺数,直到Re=10000为止。在此Re范围内的曲线BCD,仍可用式(4-8)来表示,但式中的K和x并不恒定,由Re求中要直接根据图4-8。由求N可用下列关系:N=中pn3D6。当流动变为充分湍流时,即Re>10000以后(线段DE),功率函数曲线变成水平线,此时流动与雷诺数和弗劳德数都无关,由曲线的DE段可得
(4-7)
中=Po=6.1
所以对于有挡板的典型构型搅拌器,Re>10000时
(4-11)
于是
N=6.1pn3D5
(4-12)
在无挡板的搅拌槽中,打漩现象随雷诺数的增大而逐渐显著,弗劳德数变得重要。
4-8)
图4-9所示为与典型构型相同唯独没有挡板的搅拌器的功率函数曲线。
由图4-8与图4-9的比较可知,对于有挡板和没有挡板的搅拌系统,功率曲线一直到
几
Re≈300(各曲线的ABC段)时都一样,这表示打漩现象尚未明显。当打漩加剧,功率函
何
数曲线陡然下降,图4-9中的功率函数曲线CD段有一个改变着的负的斜率,亦即式(4-7)中的指数x为一变动着的负值。在充分发展的湍流情况下(Re>10000),功率函数曲线从斜率为负而趋于成为水平线(线段DE),功率函数中近于一个常数值。
层流区
过渡区
湍流区
103
Re<300时, =Po=N/pn3D
102
FA
Re≥300时, = Po/Fr(α-1gRe)/β
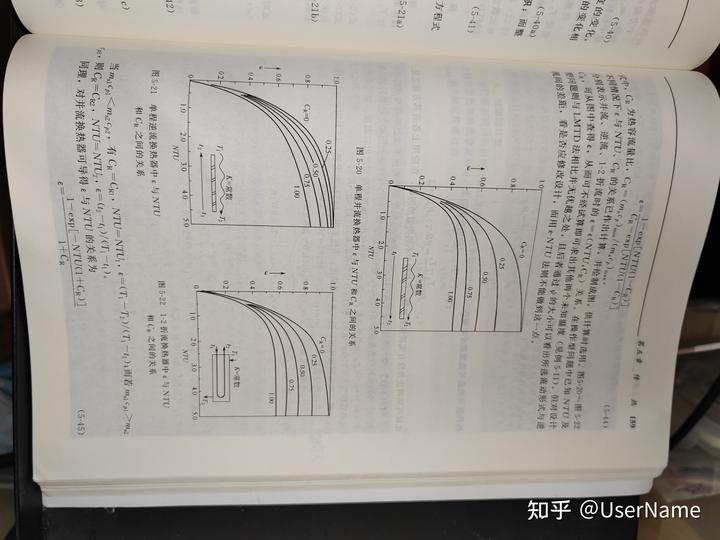
↑
010
B
D
E
1
10
102
103
104
105
Re→
图4-9典型搅拌器构型的功率函数曲线(无挡板)
1.30化工原理
对于无挡板的搅拌系统,当Re<300,=Po,故从功率函数曲线上读出后
可用下列关系:N=中on3D5。
表示
对于无挡板的搅拌系统,当Re≥300,中=Po/Fr>。将实验数据整理后可知y
【例4-2】有一个具有
y=(a-lgRe)/β
心,转速为100r·min1。
于是得
度为945kg•m3。槽中液
Po
=Fr(a-ale7a
功率。此搅拌系统符合
N=pon3D5 Fr(a-lgRe)/3
解
R
几种搅拌器的a、3值见表4-2。
搅拌器形式表4-2几种搅拌器的α值与β值[用于式(4-14)及式(4-15)]
由于Re>300,而搅
功率函数曲线
图4-9上查得中=2,再计
aβ
搅拌器形式
透平式,6平片(典型构型)图4-9
1.0
功率函数曲线
40.0螺旋桨式,T/D=4.5
螺旋桨式,T/D=3.3
图4-10中的曲线B
图4-10中的曲线C
对于本题的搅拌器构型,
1.718.0螺旋桨式,T/D=2.7
0
图4-10中的曲线D2.3
各种不同构型的搅拌器,各有其不同的功率曲线。图4-10所示为螺旋桨式搅拌率曲线。其他可参阅手册或有关搅拌器的专著。
103
曲线螺距TDH/DH/T
A2:13.31.01.0
B2:13.31.01.0
102
C1:14.51.0
选学内容
1.0
D1:12.71.01.0
10
4挡板,WB/T=0.1A
一、搅拌器放大的
无挡板
无挡板B
设计一个设备若仅从理
C
亦不见得都能适用。针对某
无挡板D
设备进行试验,在试验中使
10
102
10310
105
种放大,并非单纯地将设名
Re=D2np/μ
径等尺寸增大以外,至少
图4-10三叶片螺旋桨式搅拌器的功率函数曲线
放大问题在化工设计
理这种问题的途径与所根
上面的讨论,仅限于搅拌器所消耗的净功率。考虑到电机与机械上的各种损失,实概念。
功率应较此为大,约等于净功率值除以0.8所得之商。
放大时使用的一种重
系统(原型)之间的三种
【例4-1】有一个具有6个平片的透平式搅拌叶轮,其直径为3m,转速为10 rmi
若两设备的大小不同
搅拌槽直径为9 m。叶轮距槽底高度为3 m。槽壁上有4块挡板,挡板宽度为0.9m,液此两设备便达到几何相似
深度为9m。液体黏度为1000cP,密度为960kg·m3。计算所需功率。
似。如果两套设备不但几
解此搅拌器系统符合典型构型,其功率函数曲线即为图4-8中的曲线。先计算R何相似与运动相似以外,
对于两个搅拌系统
Re=D2np32×(10/60)×960
tw/D、…]都相等,而
1000×10-3=1440
从图4-8中读出Po==4.5,所以
系统的剪切力相似,需
何尺寸D放大后,若
N=Popn3D5=4.5×960×
显然,两者不能同时成
×35=4860W(或4.86 kW)
出这一控制性特征数,
出后,求N
第四章搅拌131
可知y可用下
【例4-2】有一个具有6个平片的透平式搅拌叶轮,其直径为50.cm,位于槽的中心,转速为100 r•minl。槽径为1.5m,槽是平底而无挡板。液体黏度为200cP,密
14-11度为945 kg*m3。槽中液体深度为1.5m,叶轮距槽底的高度为50cm。计算所需
功率。
解此搅拌系统符合典型构型,但没有挡板,其功率函数曲线如图4-9所示。
(4
re=D2np0.52×(100/60)×945≈1970
200×10-3
(4)5
由于Re>300,而搅拌槽无挡板,故有打游现象,因此要用式(4-15)计算。先从
图4-9上查得=2,再计算
曲线
Frn2D_(100/60)2×0.5
=0.141
g
9.81
曲线C
对于本题的搅拌器构型,式(4-15)中的a=1.0,=40.0。故有
线D
N=中on3D5Fr(a-1gRe)/3
2.318.
=2×945×()
×0.55×0.141(1-lg1970)/40
式搅拌器的项
=2×945×1.6673×0.55×0.141-0.0574
=306W(或0.306kW)
选学内容
第三节搅拌器放大
一、搅拌器放大的基础
设计一个设备若仅从理论出发,则很多具体情况与特殊条件都难以考虑,现有的经验公式或关系曲线亦不见得都能适用。针对某一实际目的而设计一搅拌系统,就会遇到这种困难。常用的解决办法是以小型设备进行试验,在试验中使表示工艺特征的参数达到生产的要求,然后将此小型设备放大到生产规模。这种放大,并非单纯地将设备的尺寸增加若干倍,还包括一系列操作条件的相应变化。例如搅拌器,除了直径等尺寸增大以外,至少还要确定出转速应如何改变。
放大问题在化工设计中常会遇到,搅拌器的放大是比较简单而又典型的一种。此处所述,仅为处理这种问题的途径与所根据的原则,目的是使读者得知有此种解决问题的方法,并对此获得一些初步概念。
失,实际的
放大时使用的一种重要工具是相似原则。在液体搅拌系统中,需要考虑试验系统(模型)与实际生产系统(原型)之间的三种相似:几何相似、运动相似、动力相似。
若两设备的大小不同,但其中一设备任何两部分的尺寸之比与另一设备相应两部分的尺寸之比相等,
rmin
此两设备便达到几何相似,犹如两个三角形的对应边长之比相等即为相似。构型相同的设备都算是几何相
m。液体
似。如果两套设备不但几何形状相似,而且在各对应点上的速度之比也相等,它们便达到运动相似。除几何相似与运动相似以外,如果在各对应点上的力之比也相等,便说它们达到了动力相似。
算Re
对于两个搅拌系统,其几何形状可以使各个几何特征数之值[如式(4-6a)中的S1=T/D、S2=w/D、…]都相等,而达到完全的几何相似;但不同的动力相似,则通常是相互矛盾的。如为使两搅拌系统的剪切力相似,需使两系统的Re=D2np/μ值相等;为使重力相似,需使Fr=n2D/g值相等。当几何尺寸D放大后,若按Re值相等,需使转速保持nD2不变;但按Fr值相等,则需保持n2D不变;显然,两者不能同时成立,在放大中只能满足占控制地位的动力相似——其特征数的值相等。为了找出这一控制性特征数,可以通过逐级放大试验而得到;在几个(一般用三个)几何相似、大小不同的
变
怪热的
物料相变过程
#性问题
(例如搅拌或泵送流体)
成密度的差异,也会发生
第五章传热
伴随有自然对流给热,
(三
辐射
伴
辐射是一种以电磁
体在放热时,热能变为
第一节概述
分地或全部地被吸收,
的转化,这是热辐射区
需要任何物质作媒介。工业生产中的化学反应过程,通常要求在一定的温度下进行,为此,必须适时地输入或
一、传热在工业生产中的应用
是,通常只有在高温下输出热量。此外,在蒸发、蒸馏、干燥等单元操作中,也都需要按一定的速率输入或输出
实际上,上述三种
量。在这种情况下,通常须尽量使其传热优良。还有另一种情况,如高温或低于室温下操
经常遇到热量从热流体的设备或管道,则要求保温,以尽可能减少它们和外界的传热。至于热量的合理利用和废热
的给热。的回收,对降低生产成本、保护生态环境等,都具有重要意义。这些都与热量传递(简称
三、传热速率与
传热过程的首要
热)相关。因而传热是最常见的工业过程之一。传热出
两种方式表述。
热的传递是由于物体内部或物体之间的温度不同而引起。根据热力学第二定律,热
二、传热的三种基本方式
热量
(1)热流量单
是自动地从温度较高的物体传给温度较低的物体;只有在消耗机械功的条件下,才有可能
W)
表示。传热面积
低温物体向高温物体传热。本章只讨论前一种情况。传热的基本方式有三种,已在物理学中
(2)热通量(或
论及;以下做简短回顾,然后讨论其在工业应用中的问题。
位为
W·m2)表示
两种表述方式
(一)热传导
热量从物体内温度较高的部分传递到温度较低的部分或者传递到与之接触的温度较低的另一物体的过程称为热传导,简称导热。这一过程中,物体各部分之间不发生宏观上的相
位移。
(1)需要有温差和导热介质存在
)周、液、气体者呵作导,腿
式中,A为传热面
3纯粹的导
从微观角度来看,气体、液体、导电固体和非导电固体的导热机理各不相同。气体的导
热流量Q和热
热是气体分子作不规则热运动时相互碰撞的结果。气体分子的动能与其温度有关:高温区的
积dA,用于局部
在静止的
分子运动速度比低温区的大。能量水平较高的分子与能量水平较低的分子相互碰撞的结果
的平均值。
固体内部
热量就由高温处传到低温处。对于固体,良好的导电体中有相当多的自由电子在晶格之间
对于不同的传
动。正如这些自由电子能传导电能一样,它们也能将热能从高温处传递到低温处。而在非
I=U/R的形式电的固体中,导热是通过晶格结构的振动(即原子、分子在其平衡位置附近的振动)来实现的:物体中温度较高部分的分子因振动较激烈而将能量传给相邻的分子。一般通过晶格振传递的能量要比依靠自由电子迁移传递的能量慢得多,这就是良好的导电体往往是良好的导
其中,传热温差热体的原因。至于液体的导热机理,有一种观点认为它定性地与气体类似,只是液体分子间
传热速率则与电的距离比较近,分子间的作用力对碰撞过程的影响比气体大得多,因而变得更加复杂。更
概念,会对传热的研究者认为液体的导热机理类似于非导电体的固体,即主要依靠原子、分子在其平衡位置
的振动,只是振动的平衡位置间歇地发生移动。
在传热过程
总的来说,关于导热过程的微观机理,目前仍不够清楚。本章中只讨论导热现象的宏观
规律。
(二)对流
对流是指流体各部分质点发生相对位移而引起的热量传递过程,因而对流只能发生在
一、傅里叶
体中。在工业生产中经常遇到的是流体流过固体表面时,热能由流体传到固体壁面,或者
(一)温度
固体壁面传入周围流体,这一过程称为对流给热,简称给热。当用机械能使流体发生对
由于要有
(或空间)各点
外作用
第四章搅拌133
42若习题4-1中的搅拌槽壁上有4块垂直挡板,每块宽度为18cm,其他条件不变。求此时搅拌器所需若用习4-1中的搅器系统来搅拌一种乳胶配合物,该液体的黏度为120000cP,相对密度为1.12。功率。
4-3求搅拌功率。本题安装挡板对搅拌功率有何影响?
符号说明
单位
符号意义
单位
符号意义
m'
D
叶轮(搅拌桨)直径
m
搅拌槽中液体体积
挡板宽度
m
压头
m
Wb
H
叶片宽度
m
叶轮距槽底的高度
m
w
Hi
Hi槽内液体深度
m
a
指数[见式(4-13)和式(4-14)]
K.K常数
β
指数[见式(4-13)和式(4-14)]Pas
功率
μ
液体黏度
N
kgm3
n
转速
s1
液体密度
N.m1
m3.s-1
a
液体表面张力
Q
液体体积流率
叶片长度
m
搅拌功率函数
r
了
叶轮中心盘的直径
m
Fr搅拌弗劳德数Dn2/g
T
搅拌槽直径
m
po搅拌功率特征数N/pn3D5
ms-1
re搅拌雷诺数D2np/μ
aut
叶轮外缘速度
参考文献
1王凯等.搅拌设备.北京:化学工业出版社,2003
2陈志平等.搅拌与混合设备选用手册.北京:化学工业出版社,2004
吕维明等.液体搅拌技术.台北:高立图书有限公司,2008
132化工原理
模型试验装置中,改变转速,确定达到预定指标(拌要求的转速,检验这一转符合的值相等。
应当指出,由于搅拌槽中的流体流动甚为复杂,逐级放大试验的结果可能表明;所考虑的特都不保持恒定,而需针对某特定的工艺要求另外找寻在放大时保持不变的组合量。由于它们可能
若习题4-1中的搅拌槽壁
(故并非特征数),而统称为放大判据。搅拌系统的放大判据,除上述Re及Fr以外还可考虑:4-2功率。
叶)外端速度u1nD;单位体积流体的输入功率N/V等。现用以下例子,说明如何通过逐级放
若用习题4-1中的搅拌器
放大判据。
4-3求搅拌功率。本题安装挡
二、搅拌器放大的实例
【例4-3】某合成洗涤剂生产过程中需用到的搅拌器,已在符合典型构型(有挡板)的模型符号意义
叶轮(搅拌桨)直径
取得满意的结果;搅拌槽直径T=0.225m,而生产规模T'=2.7m。为进行逐级放大试验,分别了个上一模大构,的进行验及工D
压头
叶轮距槽底的高度
速见表4-3。求生产装置应设定的转速。
槽内液体深度
表4-3搅拌槽的尺寸及转速
K.K'常数
搅拌槽号
功率
槽径T/m
叶轮直径D/m
N
1
转速n/rmin
转速
n
0.225
0.075
液体体积流率
1275
Q
2
0.45
0.15
叶片长度
3
632
r
叶轮中心盘的直径
0.90
0.30
320
T
搅拌槽直径
解为找出在逐级放大中保持数值恒定的放大判据,对已提出的4个判据分析如下。
叶轮外缘速度
ut
①Re=D2np/μ,其值不变即D2n不变;因对同一种料液μ、p一定。
②Fr=Dn2/g,其值不变,即Dn2不变;因g为常数。
③u1=Dn,其值不变即Dn不变。
1王凯等搅拌设备北京:
2陈志平等搅拌与混合设备
④N/pon2D/D3D2n3,当Re>200~300,对于Re值不是很大的变化范围,可认为为能
3吕维明等液体搅拌技术
(见图4-8),故N/V是否不变,可用D2n3代表。
对逐级放大装置的D2n、Dn2、Dn、D2n3做计算,见表4-4。
表4-4D2n、Dn2、Dn、D2n3的计算
搅拌槽号
D'n
Dn
1
D2n3
7.2
12.2×104
2
95.6
11.66×10
14.2
5.99×10
3
94.8
5.68X10
28.8
3.07×10
96.0
2.95×10
由表4-4可知,保持基本不变的是Dn,即叶轮的外端速度u1;对此,转速n与轮径D成反出!产装置的叶轮直径D'=2.7/3=0.9m,为达到与模型试验同样搅拌效果的转速n'应为
n'=n=1275×0.075
0.9=106 rmin
注意:本例中的放大判据不是特征数。但很多试验表明,放大判据以特征数居多。
习题
1搅拌器系统有一个带6个平片的透平式叶轮,位于搅拌槽中央,槽径为1.8m,推动器直径为叶轮在槽底以上0.6m。槽中装有50%烧碱溶液,液体深度为1.8m,液体温度为65℃,在此温液体的黏度为12 cP,密度为 1500 kg•m3。叶轮轮速为 90 r•minl,壁上没有挡板。求搅拌器功率。
物料变温付程
物料相变过程
加强传热
(削弱(保温)
载技的是
起冷却)
选用原剂:(1)温度易调控(2毒性);
T的对而传,称为自然对热在强制对流热的时一般
随有自然对流给热,只是后者的传热速率往往要小得多
(三射
伴随热能与辐射能的转换
不易燃易
一
水饱和水蒸气
爆不腐蚀
B价格便宜
体在放热时,热能变为辐射能,以电磁波的形式发射而在空间传播,当遇到另一物体,则部
来源容易
地或全部地被吸收,重新又转变为热能。因而辐射不仅是能量的转移,而且伴有能量形式
地输入或
的转化,这是热辐射区别于热传导和对流的特点之一。此外,辐射能可以在真空中传播,不需要任何物质作媒介。物体(固体、液体和某些气体)虽经常以辐射的方式传递热量,但
是,通常只有在高温下辐射才成为主要的传热方式。
不需温差
或输出热
t
温下操作
实际上,上述三种传热方式,很少单独存在,而往往是三者不同主次的组合,如生产中
月和废热
经常遇到热量从热流体通过间壁向冷流体传的过程它包括通过间壁的热传导和壁两侧
(简称传
的给热。
三、传热速率与热阻
导热+对流1称为对流传热
热过程
热流方向:高温向低温进行传递
传热过程的首要问题是确定传热的速率。不论是哪种传热方式,传热速率都可以用以下
两种方式表述。
热量总
KwkJ
可能由
(1)热流量单位时间内通过全部传热面积传递的热量,以符号Q(单位为Js1,即
W)
理学中
表示。传热面积与热流方向垂直,类似于与流体流动方向垂直的横截面积。(2)热通量(或热流密度)单位时间内通过单位传热面积传递的热量,以符号q(单
位为W·m2)表示。传热面上不同的局部面积其热通量可以不相同。
两种表述方式之间的关系为
低的
dQ
勺相对
dA
Q-06
(5-1)
材理荷
式中,A为传热面积,m2
的导
热流量Q和热通量q以后要经常用到,应注意其间的区别和关系。其中,q基于微元面
区的
积dA,用于局部地区;而Q是对整个传热面积A而言,当局部的q不相等时,Q为关于A
结果,
的平均值。
间运
对于不同的传热方式,传热速率的表达式也不相同,但一般可以转化成电学中欧姆定律
非导
I=U/R的形式
I-TwaF
实现
传热温差、
传热推动力
振动
传热速率=
热阻
传热阻力
Q2-
的导
其中,传热温差为传热的推动力,与电压U对应;而热阻为传热的阻力,与电阻相对应;
子间
传热速率则与电流I对应。正如欧姆定律在电学中得到广泛应用,在传热过程中引入热阻的03.tt
更多
概念,会对传热问题的求解带来很大的方便。R3
立置
在传热过程中,通常传热温差较易决定,传热速率的问题主要是确定热阻。
总边推动力at=T-t
观
第二节热传导
总热阻:R=R1+R2+R3
传速率Q=Q1=a2=Q3
一、傅里叶定律
温度分布:对应温差大小,决定:
导执速率大小
Ri
流
推动力:温差
由
由于要有温差才会发生传热,故需知道物体内的温度分布才能计算其热传导速率。物体
(一)温度场和温度梯度
流
(或空间)各点温度在时空中的分布,称为温度场,可用通式表示如下。
136
化工原理
=f(x,y,z,0)
式中,t为某点的温度;x,y,z为这一点的坐标;为时间。
气体的热
一维稳定温度场
有气体存在
女
200 MPa)
e
温度随时间而改变的温度场称为不稳定温度场;若各点的温度均不随时间而改变,则
为稳定温度场,其一般数学式应在式(5-2)中去掉0。
温度相同的点所组成的面称为等温面。因为空间任一点不能同时有两个不同的温度,
图5-3月
以温度不同的等温面彼此不会相交。
4t=0
30
沿着等温面温度不发生变化,故也没有热量传递;而沿与等温面相交的任何方向移
28
温度都有变化,因而也有从高温到低温的热量传递。温度随距离的
26
化率以沿等温面的法线方向为最大。两等温面的温度差与其
24
0
t-△
法向距离△n之比称为温度梯度,某点的温度梯度为△n趋近于零时
22
1n-
an
极限值,即
好快子
At
at
1X..
20
0
fdA
lim
△n→0
△n
an
18
√
图5-1温度梯度与
温度梯度是向量,其方向垂直于等温面,并以温度增加的方向
16
热流方向示意
正(见图5-1)。偏导数的意义是指只考虑法向上的温度差。
14
(二)傅里叶定律的表达式
导热的微观机理虽不够清楚,但其宏观规律可用傅里叶(Fourier)定理描述,即导
12
n=1,1时,=入[J]
0
2
导热系数
通量q与温度梯度at/an成正比
小一
dQ
dA芸
q=-
(5-3
1一无水甘油
入为物质
式中,X为比例系数,称为热导率,W·m1·K1或W·m℃-1
6一苯胺;7
而负号表示热流方向与温度梯度的方向相反;此外,热流方向与等温面垂直。
11一异
的物理属性
15-
、热导率
热导率(也称导热系数)表示物质的导热能力,是物质的物理性质之一,其值常与物
不同物
的组成、结构、密度、压力和温度等有关,可用实验方法求得。下面分别叙述固体、液体
气体的热导率。
(一)固体的热导率
1物质越纯,
③片-液)2同一材料P越大,入个(与物质内部结构有关)
与物质物理
金属是良好的导热体。纯金属的热导率一般随温度升高而略有减小。金属的纯度对率的影响很大,例如纯铜在20℃下的热导率为386 W·ml·K1,而若含有微量的砷,
剧下降到一半以下。
入导体非导体>入液体>入气体
金属的水。
非金属的建筑材料或绝缘材料的热导率与其组成、结构的致密程度以及温度等有关。
常值随密度的增大或温度的升高而增加。
y1-U.M/Y
北65>0
大多数均一的固体,其热导率在一定温度范围内与温度约成直线关系,可用下式表示式中,.为固体分别在温度t、273K(0℃)时的热导率。Wm·K1或WmC;
λ=Ao(1+at)
度系数,对大多数金属材料为负值,而对大多数非金属材料则为正值,K-1。
附录四列出了一些常见固体材料的平均热导率。
(二)液体的热导率
非金属液体以水的热导率最大。除水和甘油以外,绝大多数液体的热导率随温度的
M
而略有减小。一般来说,纯液体的热导率比其溶液的热导率为大。
图5-2所示为几种常见液体的热导率及其与温度的关系
(三)气体的热导率
三、
(一
如图
第五章传热137
气体的热导率很小,不利于导热而利于保温。如软木玻璃棉等就是因其细小的空隙中
00MPa)或很低(如小于 2.7 kPa),其热导率实际上与压力无关。
图5-3所示为几种气体的热导率及其与温度的关系
30
传热速率随面积的个而
28
69
16
8
27
0
9
26
67
8
65
24
4
7
63
0
.ou.
22
13
.E.0
6
5
61
20
5
3
5
59
E
6
18
7
4
6
57
4
16
89
10
3
3
55
14
13
IT12
(H2)≈10(Ar)
14
53
2
2
12F
/
15
16
1.163
0
2040
60
80100120140
02004006008001000
/℃图5-2
液体的热导率
图5-3气体的热导率
1-无水甘油;2-蚁酸;3一甲醇;4-乙醇;5-蓖麻油;
1一水蒸气;2一氧;3一二氧化碳;
6-苯胺;7-乙酸;8-丙酮;9丁醇;10一硝基苯;
4一空气;5一氮;6一氩
11一异丙苯;12一苯;13一甲苯;14—二甲苯;
15一凡士林油;16一水(用右边的坐标)
不同物质的热导率的大致范围如图5-4所示。
1000
√
银、铜
固体100
钠金属
液体钢
氧化物金属
LX.1-U.M/Y
10
固汞
体
非
1
金
水属
液体
纤维非金
绝热
He、H2
属
材料
气
真空
0.1
塑料
体
绝热
木材
油
发泡
CO2
材料
0
x b
材料
0.01
图5-5单层平壁的稳定热传导
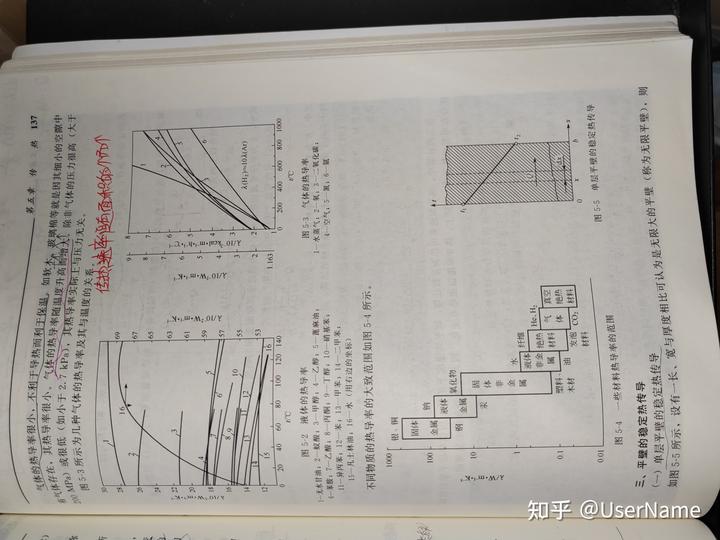
图5-4一些材料热导率的范围
三、平壁的稳定热传导
如图5-5所示,设有一长、宽与厚度相比可认为是无限大的平壁(称为无限平壁),则
(一)单层平壁的稳定热传导
双层
140化工原理0.001
t2+t-(1305-2048x)=0【例5-3】
t=-1000±√3.61-4.1x×103
2
舍去负值,计算得平壁内的温度分布如表5-1所示。
表5-1平壁内的温度分布今测得
0.20.3
0.4
0.10.5
上的温度。
0670
543
404
解参
距离x/m789
250
900
温度t/℃640
510
380
Q-b1
900770
250
按温度直线分布式(a)AIA
按此温度分布作出的曲线如图5-6。由图可知,考虑随t的变化,温度分布曲线稍是由式(5-5)
行的。
(二)多层平壁的稳定热传导
若平壁由多层不同厚度、不同热导率的材料组成,其间接触良好,即接触热阻可以略,如图5-7(以三层平壁为例)所示。设各层的厚度分别为b1、62及b3,热导率分别各层温度降
1、2及3,壁的导热面积皆为A,各层的温度降分别为At1(=t1—t2)、At2(=t2-t)1△t3(=t3-4)。由于在稳定导热过程中,通过各层的热流量相等,故
Q=1At1-t2Ati
耐
b1bi/1A Ri保
1000建
=λ2At2t3△t2
△
1b2
b2/2A
R2四、圆
=λ3At3-t4At3_
At3在工业
b3R3
。所示。若圆
(55)
应用合比定律可得径向的一维
Q=At1+△t2+△t
0b1 b2 b3
x/mλ1A2Aλ3A
图5-7多层平壁的稳定热传导且传热面A
△t1+△t2+△t3t1
R1+R2+R33
R与平壁不同
推广到层平壁i=1
哪层热阻大哪层温差大(5-6a)
半径r成正
反之成立。是相等的
.Q
_t1-tn+1_总导热温差
R式(5-7a),
总热阻(5-6)
式(5-5)及式(5-6)表明,应用热阻的概念可以简化多层平壁导热的计算。注意以上
i=1
接触良好而忽略两层平壁之间的接触热阻,若不能忽略,则应在总热阻中加入。
式(5-5)还表明,对于串联的多层热阻,各层温差△t;的大小与其热阻R;成正比。这
一概念在例5-3中要用到,今后也很有用。故
热是x向
公式g--t2 t-1
第五章
传
因此平壁内的温度分布可用下式表示b/Am x/m热
139
t=900-2=900-
入m2050.x
9001.575
=900-1300x(a)
育化成800
(5-1a)700
600λ为变数
500λ为常数
(5-4)400
300
200
(5-4a)0
0.10.20.30.40.5
x/m
图5-6例5-2附图
砖壁当x=0时,t=t1=900℃;当x=0.5m时,t=t2=250℃。在直角坐标上将此两点
相连而得到的直线就是热导率为常数时的温度分布线。如图5-6所示。
的导(2)如取热导率为温度的线性函数
q=-1.0(1+0.001t)
分离变量并积分gdx--(1+0.01)dr
的温q(1+a.g1)+c
(b)
t)将边界条件代入上式
当x=0,t=t1,
有o=-(n+g)+c
(c)
当x=b,t=t2qb=-(1+0.901)+c
(d)
得
由式(d)减式(c)消去C,可得[1+0.01()](-)
将t1=900℃,t2=250℃代人上式得
0.5×[1+0.001×(
900+250)7
×(900-250)=2048W·m2
与以上取平均温度下热导率的结果相同。将值代式(d)得C=1305,再由温度
分布式(b)得
△t
)62
R:
d=d
平壁A为常数
只沿厚度方向(图中x向)有热流,或说温度只沿垂直于壁面的x向变化,即导热是,138化工原理
Q-Att
可简化成而得
岩单层壁导速率公式
的一维问题;式(5-3)中的an=-
因此平壁内的温度分
若给定边界条件:x=0时,t=t1x=b时,t=t2;如图5-5所示,积分后可得
A(t1-t2)
q=
b
对于无限平壁,通过导热面各局部面积(等温面各点)的热通量相等,式(5-1)可简化成ts:t温布dQ_Q
q=
dA A(5-
Q=Aq
即平壁温度分布线性的
结合以上两式可得AA(1-12)
Q=b
式中,A为平壁壁面面积,m2;Q为通过全部壁面面积的热流量,W。
式(5-4)可改写成“传热推动力/热阻”的形式
t1-t2At
Q-b/(A)R(5-a)
式中,R为无限平壁的导热热阻,R=b/(A)。
对于工业平壁,常应用上述无限平壁的结果,而无需校正。当x=0时
【例5-1】厚度为230mm的砖壁,内壁温度为600℃,外壁温度为150℃。砖相连而得到的直
的热导率可取为1.0W·m1·K1(即1.0W·m1·℃1),试求通过每平方米砖壁的(2)如取热
热量。
解由式(5-4)分离变量并积
QA(t1-t2)1.0×(600-150)
q-A=1960W·m-2
0.23
在工程计算中,热导率通常可作为常数处理,取平均温度下的值,所以单层平壁内的温
度分布可看成是直线。实际上,热导率随温度略有变化,因而温度分布线略呈弯曲
【例5-2】平壁厚500mm,若t1=900℃,t2=250℃,热导率λ=1.0×(1+0.001将边界条件代
W·mK1,试求沿平壁厚度的温度分布和导热通量。当x=0
(1)热导率按平壁的平均温度t取为常数;(2)考虑热导率随温度而变化。有
解(1)热导率按平壁的平均温度tm取为常数当x=b
tm900+250=575℃得
热导率的平均值2
Am=1.0×(1+0.001×575)=1.575W.mK-1由式(d)
减
导热通量Q_Am(t1-t2)_1.575×(900-250)
将
-A
b
在稳定导热过程中,任一等温面上的t不随时间而变化,即输入各等温面的热量与输
0.5=2048W·m2
出的热量相等。若以x表示沿壁厚方向上的距离,在x处等温面上的温度为t,则与以
分布式(b)
T一T2
:a+A(T-下)
d(2+)67
【例5-3】有一炉壁,由三种材料组成:第五章
般:16~32
耐火砖λ1=1.4 W-m-K1,b1=230 mm;传热141
保温砖2=0.15WmK1,b2=115 mm;
建筑砖λ3=0.8 W•m1-K1,63=230 mm
0.5今测得其内壁温度为900℃,外壁温度为80℃,求单位面积的热损失和各层接触面
上的温度。
解参看图5-7,应用式(5-6)不用取得过大
50=3
t1-t4
Q-b1+b2b30.23900-80
500.115
1.4×10.15×10.23820
空气是最好的佳温
0.8×1
由式(5-5)得0.164+0.767+0.288
=673w
陆
稍呈
是可△t1=QR1=673×0.164=110.4℃
t2=t1-△t1=900-110.4=789.6℃
△t2=QR2=673×0.767=516.2℃
t3=t2-△t2=789.6-516.2=273.4℃
以忽各层温度降和热阻的数值见表5-2。
△t3=t3-t4=273.4-80=193.4℃
别为
)及表5-2各层温度降和热阻
项目温度降/℃
耐火砖,厚230mm热阻/℃W-
110.4
保温砖,厚115mm516.2
0.164
建筑砖,厚230mm0.767
193.40.288
四、圆筒壁的稳定热传导
在工业生产中,常常用到圆筒形的容器、设备和管道。通过圆筒壁的热传导,如图5-8所示。若圆筒的长度远比半径r为大,可认为其内的传热是只沿
5-5)径向的一维导热,于是式(5-3)
中的
at
on
简化成而有
dt
q=—x
总推力且传热面A上各点的热通量q相等,式(5-1a)Q=Aq仍然成立,得到
总热阻Q=-λA
(5-7a)
与平壁不同的是圆筒壁的内外半径不等,其导热面积A=2πrl与
半径r成正比。在稳定情况下,通过圆筒壁内、外壁面的热流量0
a)是相等的,即Q为常数;因而q与A成反比。将A=2πrl代人
式(5-7a),分离变量,进行积分(积分限参看图5-8)。图5-8圆筒壁
6)的热传导
d =asot
Q-2nLi
trto
Qln=2πl(t1-t2)R
(5-7)
r1t1-t2
故t1-t2
t1-t2
Q=2πλlIn(r2/r1)
R
In
#22元l
0-2元9=2元
热通量:a=
-u].
142化工原理In(r2
2)为热阻。
2nA/
式中,温差(t1t2)为推动力;R
式(5-7)也可以改写成平壁导热式(5-4)的形式:
2nl(r2-r1)(t1-t2)
2=Am5-
A,Q=
In(r2/r1)(r2-r1)
对数r2-r
电抽:优:便于控制
热源
式中,6为筒壁的厚度,b=r2—rAm为均面积,Am=2rm;rmIn(r/r)
数平均半径;当r2/r1<2时,可以改用算术平均值,即取rm=(r1+r2)/2,而误差不大
2饱和水蒸汽(常用):
为
令△2、△1(△2>△1)代表任意两个数,现将不同△2/△1下,这两个数的算术平均值和缺
对数平均值做对比,见表5-3。表5-3算术平均值与对数平均值
1.51.3
优:可加热
1.1
21.013
1.005
3烟道气
1.04约1.0
4/41.10
Am算术m(对数)由此可见,在△2/△1=2时,算术平均值和对数平均值相一
2.冷源:水空气
差4%。工程计算中常能容许,故当r2/r1≤2时,可用算术
均值代替对数平均值。
热阻可按R=b/λAm来计算。3稳定传热:流体温
传热速
对于层与层间接触良好的多层圆筒壁,如图5-9(以三层圆
壁为例)所示,各层的热导率分别为1、A2及A3,厚度为b1、随位
及b。与多层平壁的稳定传导热计算式(5-6)相类比,得
△t1+△t2+△t3t1-t4
Q=R1+R2+R3R1+R2+R3(5-8a)
影响因素内因
t1-t4(5-8b)
内因不影响
b1_b2b3
①热容热
A1Am1 A2Am2A3Am3
对于n层圆筒壁黏度:
人低
图5-9多层圆筒壁的热传导Q
=t1-tn+1t1-tn+1
(5-8)
bln(rii/r)
入A导热手入:入个
2元Di
与多层平壁导热式(5-6)的差别仅是各层热阻的平均导热面积不同,应对各层分别算。式(5-8)也说明应用热阻的概念能使计算简化。
由于各层圆筒的A不同,故在稳定导热中各层的热流量Q虽相同,但热通量则不相等(与半径成反比),其相互关系为烟:1流体流动状态
或Q=2πr1lq1=2πr2lq2=2r3lq3=2πr4lq4
式中,q1、q2、q3、q4分别为半径r1,r2,r3,r4处的热通量。
r1q1=r2q2=r3q3=r4q4
【例5-4】50 mm×5 mm的不锈钢管,热导率为 16 W·m-1K-1;外包厚30 mm的矿物棉,热导率2为0.2 W·m·K1。若管内壁温度为350℃,保温层外壁温度为100℃,试计算每米管长的热损失。4流所在的相
解不锈钢管内半径r1=40/2=20 mm,外半径r2=50/2=25 mm,r2/r1<2,可按算术平均求平均半径及每米管长的平均面积研究方法—因
R
m
r2-r
5-7
An(
)/2,而误差不大
热源
个数的算术平均值
优便空制使用方使比较情洁贵用他和冰片(常月):调的和蒸山的在姿就可以控制库
加热速度
缺:冷凝传热能达的温度受压强控制
1.1
约1.0
3烟道气:优:可加热高温度缺:传热速度慢
匀值和对数平均值相
<2时,可用算术平
2
冷源:水、空气.冷冻盐水图5-9(以三层圆
3稳定传热:流体温度只随位置改变,不随时间改变
(传热速率为常数)Q=Q2=Q3
及A3,厚度为b1、
相类比,得
:随位置、时间变为变量
4
+R3
(5-8a)
影响因素内因、外因(5-86)
内因不影响
2712-9则小
黏度:低占流体小占流体(5-8)
n)
热系数入:入个,2个应对各层分别计
但热通量qi
则升
:1流分流动状态:小湍>小层流
2引起流体对流原因
以强制对流子自自对流
3流体有无相变化对心的外包厚30mm
@长相书
影响:有相变>无相变
小液气
层外壁温度为
©影响
2/r1<2,可按
化工原理
给热速
144
第三节两流体间的热量传递
流体的速度
上可组合成
前已提及,工业上处理的物料多为易于输送的流体。当流体被加热或冷却时,一般用另率等热物性
一、两流体通过间壁传热的分析
一种流体来供给或取走热量。这另一种流体称为载热体;其中用于加热的称为加热剂,常用通量q与壁
的有水蒸气、烟道气等;用于移除热量的称为冷却剂,常用的有冷却水、空气。在大多数情得到较简单
此式相当于
管(称为换热管)管壁的两侧流过,热流体将热量传给壁面,通过管壁,再从管壁的另一侧
比例系数a
将热量传给冷流体。图中,热流体走管内,其温度沿壁面由T1逐渐下降到T2;冷流体走W·m-2·℃-1
外,其温度由t1逐渐上升到t2。热、冷流体沿壁面平行流动,方向彼此相反,称为逆流即相当于图
若方向相同,则称为并流。
而对间壁右
给热时
一种局部
T
T2
一般情况
da
平均温度
平
面的平均
x
←dx
热、
故即使将
t1
质。因此
图5-11套管换热器示意
即
上述换热过程中,既要考虑通过固体间壁的导热,又要考虑间壁两侧与流体的给热,而
二、
且往往后者更重要。下面着重讨论这一问题。
热、
通常,间壁两侧的流体都作湍流运动,湍流区中流体直接携带热量的对流传热,因流体质点的激烈脉动、混合而热阻很小;紧贴壁面处的层流底层(因为很薄,也形象地
形式。在
称为“膜”),则只能依靠热阻相对大得多的导热方式传热;故膜虽薄,却是给热的主要很小的管
热阻所在。
也相等,
上述传热过程可对局部壁面放大观察,如图5-12所示,相当于图5-11在离热流体进口距离为x的dx段、传热面积为dA处的放大。间壁两侧为热、冷两流体的层流底层(为示出它,其厚度放大了很多倍),两边再向外经过过渡层,达到两流体的湍流主体。左边的热
写成串联
流体,以△T=T-T的温差为推动力,传热给壁面;再消耗温差△tw=Tw-tw,以导热方式通过间壁;然后又以给热方式传给冷流体,其温差为△t=tw—t。图中示出,在两侧的给热中,由于膜内是主要热阻所在,故占给热温差(T-T)或(tw-t)的主要部分。从温
式(5-10
度分布情况可以了解各串联热阻的相对大小[见式(5-5)]。
它由三
而成。
也折算成某一膜厚,则热、冷流体的给热热阻所相当的总膜厚在图中示出为1及2,称为当量膜厚。于是,可将复杂的给热现象转化成通过当量膜厚的导热问题;这样虽然在概念上令K=
可使给热问题得到简化,但由于当量膜厚是虚拟的,并不能直接测定,给热速率的问题还需另寻其他途径解决(见本章第四节)。
可得


















K
一侧的
Aml=2rml×1=2π(0.025+0.02)
第五章传热143
2
=0.141m2
状态(热状态)
rm2=0.055-0.025
In(0.055/0.025)=0.038m
每米管长的热损失为
Am2=2rm2×1=0.239m2
△
=b1-+、b2
0.005
350-100
16×0.141+0.03
250
界层内;
0.2×0.239
250
0.0022+0.62760.6298=397W
注意:钢管壁的热阻只占总热阻的0.0022/0.6298=0.0035,而可忽略。
【例5-5】求例5-4的温度分布。
解已给定的温度是管内壁t1=350℃,矿物棉层外壁t3=100℃。管外壁亦即矿物
层内壁的温度t2可由温差与热阻成正比的关系得出
P:
350
300
↑250
e200
150
常温水的源
100<
2025303540455055
r/mm)
强制湍流的
图5-10例5-5附图
3p.
t1-t2管壁热阻
t1-t3总热阻=0.0035
350-t2=0.0035(350-100)=0.9℃
t2=349.1℃
令矿物棉层内半径r处的温度为t,为求t与r的关系可用式(5-7)的第一个等式
Q=2l(t2-t)
In(r/r2)
代人已知数值
所以
397ln(r/25)=2×0.2×1×(349.1-t)
t=349.1-316ln(r/25)
(a)
将计算结果列成表5-4。
0.4
表5-4计算结果
r >r/mm
45
50
55
1/℃
25
30
35
40
130.1
349.1
291.5
242.8
200.6
163.4
100
作成图,如图5-10所示。由式(a)或图5-10、表5-4可知,圆筒壁内的温度分布在取入为常数时也并不是线性的。
对流传热=“热传导+热对流”
矿物棉层内半径2
其速度与流体流动状态、流体性质状态(热状态)固体壁面等均有关。
每米管长的热损失为
4b2
b1×
对流传热的热阻全部在此传执边界层内;
注意:钢管壁的热阻
求例5-4
八√主要集中在层流层内
解已给定的温度是
【例5-5】
层内壁的温度t2可由温
小研究方法因次分析法
联式:Na=Re=P=
OGr:
M
低占液体的界定:其黍占度2倍常温水的季度1、无相变低占流体在圆形直管内强制湍流的对流传热系数关系式:Nu=0.023Re.8P1特性尺L=d内,d>50
2宝性度:
令矿物棉层内半径
3流体被加n=0.4.被冷却pn=0.3
代人已知数值
所以
"
液体被加热时被冷却时的小
0.4
s
将计算结果列成表5-4。
气体
rmm
作
25
Q-dSatAt
Ys热对流的推动力
热对流阻力
给热速率与许多因素有关。如影响膜厚的有
第
小对流传热系数膜系
体的速度、黏度、密度及壁面的几何特性(以
0LW
可组合成雷诺数);影响膜内传热性能的有热导90
温度3ot
等热物性参数。通常是应用牛顿冷却定律:热
Jel
0
般用另
与壁面-流体间的温差(tt)成正比,而
r
距离



















刊,常用
体
大多数情
得到较简单的形式q=a(tw-t)
(5-9)传热方
尔为热交
别从小
式相当于图5-12石边壁面被冷却的情况;式中
比例系数。称为给热系数,单位为W•m2K-1或
冷流体
另一侧Wm℃。式(5-9)也可用于流体对壁面加热,
二了
体走管
为逆流;
相当于图5-12间壁左边的给热情况
q=a1(T-Tw)
(5-9a)
图5-12热、冷流体通过间壁
而对间壁右边壁面对流体的给热写成
传热过程示意
q=a2(tw-t)
(5-9b)
给热时,无相变流体的温度会变化,物性随之变化,故。也沿传热壁面而变,即。是一种局部性质的系数。但是,在应用时以对全部传热面积A平均的给热系数为便。由于一般情况下物性的变化不是很大,在某一平均温度下取值,对工程计算是可行的;这一平均温度称为定性温度以后所称的给热系数,若不另做说明,都是指这种对整个传热面的平均值。
确定物理量取值的温度:Tt)定=进
>
热、冷流体的温度沿传热壁面而变还使得给热温差(T-T)及(t-t)发生变化,等
故即使将给热系数作为常数,给热通量q仍将随壁面位置(图5-11中的x)变化而属局部性质。因此,热流量与热通量的关系需按微分式(5-1)列出
dQ=qdA
即
顿冷却宣律
QAst
At
热,而
二、传热速率和传热系数
热、冷两流体通过间壁的传热速率,可用以前处理串联热阻的方法,得出较简单的表达
,因
形试。在稳定情况下,两侧给热及间壁导热的三个热流量相等。对于平壁(壁厚与直径之比
象地
很小的管壁亦可近似适用),三个传热面积相等,都用A代表。于是三个热通量q=dQ/dA
主要
也相等,而有t=7-7W热流体与热壁面温着
q-a3(T-T)=(T_-tw)=a3(t-t)
短管>小管
进口
为示
写成串联热阻的形式
T-t
(5-10)
的热
T-TwTw-Iw _
q-1/a1
b/1/a21/a+b/+1/a2
热方
的给
式(5-10)最右边的分子为传热的总温差A=Tt;分母为总热阻R=1/a+b/+1/a,
从温
三个分热,壁的热热1/1/和壁身的导热热6/加而成。
(5-11)
热阻
(5-12)
令K=R.1/a+b/+1/a2
1
,即++
称为
q=K(T-t)
念上
可得
还需
K称为传热系数,单位为W·m2K-,与给热系数的单位相同。但给热系数仅考虑间壁一侧的传热,而传热系数则考虑了从热流体通过间壁到冷流体的整个传热过程。前已提及,





















2薄
式(5-11)中的a1、a2、一般作为沿壁面的平均值,故K也通常认为是不随壁面位置而变化
同金
146化工原理
垢热阻
阻为
的常数。流体温度沿壁面的变化,使得总温差△t=T一t也发生变化;
按式(5-1)q=dQ/dA,将式(5-12)写成微分式
dQ=K(T-t)dA
(5-1
常见
以下讨论有关传热系数的几个问题。
1.换热管内外面积不相等的考虑
为考虑管内表面积dA1=πd1dx与外表面积 dA2 =πd2dx的差别,可将两侧给热式及测
水(u<1
蒸馏水
壁导热式写成dQ=a1 (T-Tw)dA1 =(A/b)(Tw-tw)dAw=az (tw-t)dAz
(5-10)
其中,导热面积dAw=dmdx,因换热管内、外直径d1、d2相差不多,平均直径dm可用
海水
洁净的
未处理
考虑到三个传热面的面积不同,其热通量也不相同。基于管内表面积的热通量方程可其算术平均值。
经处理
式(5-14)各项除以dA1,得到
经处理
=a1(T-Tu)-()(Tn-tn)=a2(tn-1)
dA2
硬水、
水蒸气
即
3,=a T-70(6)0-d
(5-15)
优质、
写成串联热阻的形式
若
T-TwTw-twtw-t
T-t
q1
降。所
1
a1
)(2)(2)+(2)+号2)
(5-16)
3.
令基于管内表面积的传热系数为
若
热面积
-(++)
(5-11a)
成本。
则有
同理,基于管外表面积的传热系数为q1=K1(T-t)
为
(5-12a)
大时,
换热器
基于管外表面积的热通量为ki()
(5-11b)
会占到
之,当
系数计
换热管内外的传热系数、热通量有以下关系
q2=K2(T-t)
(5-12b)
4
K2 q2 dA1 d1
K1
(见图
在传热计算中,基于管的内表面或外表面,所得结果相同;但应注意换热器制造厂
q1dA2d2
(5-17)
热时的
习惯以管外表面积作为公称面积的依据,故传热面积计算的最终结果通常用管外面积
表示。
2.污垢热阻
换热器在使用中,传热速率Q会逐渐下降,这是由于传热表面有污垢积累的缘故
由气
因此,计算K值时,污垢热阻一般不可忽视。污垢层的厚度随使用时间增厚,其热导率
由气
也不易确定,通常是根据经验估定污垢热阻,作为计算的依据。如管壁内侧和外侧的污
由煤
由水
①新管KS0-F31-0还际
2管壁
置而变化
较大56
热芬别用R1和
R2表示,由于污垢层一般很薄,因而以外表面积为基准时,
官内体
第五章传热147
流量,应
1
欢
K
d
bd+R+1
3管外流体热阻
热
(5-13)
常见流体在传热表面形成的污热阻,其大致数值范见5-5
d
(5-11e)
表5-5
流体
污垢热阻/m2·K·kW-
污垢热阻的大致数值范围 dass-nd= la
热式及间
水(n<1m/s,t<50℃)
流体二冷流体:dQ-=dlQ
污垢热阳
蒸馏水
0.09
劣质、不含油
r
(5-14)
往复机排出传势率:K1205DA-dQ
海水
0.09
0.18
dm可用
液体
洁净的河水
0.21
未处理的冷水塔用水
0.58
处理过的盐水
有机物
0.26
程可对
经处理的冷水塔用水
0.26
0.18
经处理的锅炉用水
燃料油
0.26
1.06
焦油
硬水、井水
0.58
1.76
气体
水蒸气
空气
0.26~0.53
(5-15)
优质、不含油
0.052
溶剂蒸气
0.14
诺流体容易结垢,换热器使用一定时间后,污垢热阻往往会增加到使传热速率严重下
(5-16)
降。所以换热器要根据具体工作条件,定期清洗。
3.控制性分热阻
若设法增大传热系数K,可以使传热强化,即在相同的温度条件下,用同样大的传热面积可以传递更多的热量;或对同样的传热任务可以用较小的传热面积完成,以降低
-11a)
成本。
为增大K,原则上减小式(5-11c)右边任一个分热阻都有效;但当分热阻的相互差别很
12a)
大时,总热阻1/K主要由其中最大的热阻所左右。通常,金属间壁的热阻很小而可忽略。换热器经较长期使用后,往往污垢热阻占主要部分而需进行清洗。有时,某一侧的给热热阻
11b)
站到控制地位,如在式(5-11c)的右边,与1/α2相比其他项都可忽略,则有K2≈a2。总之,当串联热阻中存在某控制性的分热阻时,为强化传热应集中力量去削减它。同理,传热系数计算的准确性,也主要取决于这个控制性分热阻。
2b)
4.传热系数数值的大致范围
换热器计算中,往往要预先估计传热系数K的值。对于工业上最常见的列管式换热器
(图5-15),K值的大致范围见表5-6。由表可知,K值的范围很大。对不同类型流体间传
17)
热时的K值,应有一数量级的概念。
厂
表5-6列管换热器中K值的大致范围
A2
进行换热的流体
传热系数K/W·m2K
进行换热的流体
传热系数K/W·m2K-1
300~5000
水蒸气冷凝到水
60~350
由气体到气体
12~35
水蒸气冷凝到油(有机液体)
由气体到水
12~60
300~900
。
水蒸气冷凝到油沸腾
由煤油到水
350左右
120~400
率
由有机溶剂到轻油
800~1800
污
由水到水
烙衡算:Q=mn(In1-In2)=Mc(Ic2-Ic1)
礼工原理
热量衡算:冷流体被加热1吸及热):Q=mcPc(t2-tH
150
热管有效长度的热流体出口处的截面Ⅱ,△
冷的(T下
d(At)
1-d
△
【例5-7】
无相变:Q=mn9(T1-T2)
mkdA-
245℃,出口
,t.1
mKA=In
别计算并流和
原引入式中的参数m,可通过对全部换热面的热量衡算而消去
K)
Q=ms1Cp1(T1-T2)=ms2cp2(12-t1)
容cp1=3kJ·k
Q
(5-22
解(1)
Q
ms2cp2t2-t1
故
mICplTI-T2
(5-22
自
代人式(5-19)中
项
(T1-T2)-(t2-t1)_(T1-t2)-(T2-t1)_At1-At
T
总传热速率基本
程
Q
Q
Q
(5-19元
再代人式(5-21),对Q解得
传扬基本方程
△t1-At
△m
即A:换热器的传热面积
Q-KA In(A/At)采用逆流:t227
st,左侧流体
Q=KA△tm
并流不可以
(5-2
6
(2)Q=
其中
AA
△m=
In(At /At
5
5-241
为换热器进、出口处的对数平均温差,当At1/At<2,可用算术平均值代替。
总热量衡算式(5-22)中,p1、Cp2为热、冷流体的种类及定性温度所确定;m、mT1、T2、t1、t2共6个参数中,已知5个可求其余的1个。
图5-13(b)所示为两流体为并流的情况,可用同样的方法导出相同的结果:式(5-23)及式(5-24);只是此时进口端的温差At1=T1-t1,出口端At=T2-t2,如图所示。应当
由本例可见
指出,并流时△1恒大于△t;但逆流时则不一定,要看mCp1(热流体的热容流量)
传递相同热流量
mag2(冷流体的热容流量)的相对大小;由式(5-22)可知,当m1Cp1<ma2Cp2,有
热剂的用量。因
△;当mp>m2p2,则△<△。为计算方便。求逆流时的对数平均温差,可取两
时,冷却剂的
端温度较大的一个作为式(5-24)中的△t1,以使分子分母都是正值。
些。同理逆流加
在热、冷流体进出口温度相同的条件下,逆流时的对数平均温差恒大于并流时的,故从
用量可以少些。
传热推动力△m的角度看,逆流总是优于并流(见例5-7)。
节省了冷却剂
当两流体之一以相变传热,其温度变化情况如图5-14所示,则相变流体的温度不沿
【例5-8】
热面变化,上述式(5-23)、式(5-24)仍适用,只是逆流或并流对△tm已无影响。
后,送再生塔
K1,试求蒸汽
温度可近似取
T
T
解使冷
12
T2
A→
加热蒸汽放出
(a)蒸汽冷凝加热无相变流体
A→
(b)无相变热流体使液体沸腾
压力为3
图5-14一侧流体相变时的温度变化
kJ-kg
0
除逆流和并流以外,换热器中两流体还有其他较复杂的流动方式,其平均温差总是介于
,故
逆流与并流之间。详情将在下面“四、复杂流向时的平均温差”中介绍。
0由饱和水蒸
利用程序计算工具计
直过,冷
应用式(5-17)换算到对管外表面积的传热系数K
K2=46.4×
第五章传热149
(1)求
百分率;
d1=46.4×
d2
热系数
20=37.1W•m2K
与本例(1)中求出的K2=37.5W·m2K相比,相差小,即可以用此方法简化近似,
三、传热温差和热量衡算
λ=45
以以上可以清楚地看到,要提高K值,就要设法减小占控制地位的分热阻。
侧污垢
的传热面积能否满足传热需要。为此,需对传热速率的微分式(5-13):dQ=K(T-)dA进
行积分。
t逆>t
d
可以
①Q、K同,A逆<A并
dAT
2A.K同,Q逆>
dr
第1
传热面A→
传热面A
(a)逆流
(b)并流
图5-13两侧流体均无相变时的温度变化
考察图5-13(a)(相当于图5-11补上温度变化),热、冷两流体为逆流,其温度T、随距离或传热面积A的增大而降低,通过微元面积dA传热后,两流体的微分温度变化dT、d都为负值。当热损失可以忽略,热流体传出的热流量与冷流体获得的热流量相等
dQ=-ms1cp1dT=-ms2cp2di
(5-18)
式中,cp1、cp2为热、冷流体的定压比热容,kJ•kgK,可取定性温度下的数值作为常数;
阻
msm为热、冷流体的质量流量,kg+s-1,稳定情况下为常数。
(5-
取负号是因为dT、d皆为负值。应用合比定律,可以从式(5-18)得到(T-t)的微分式
dT-dt
(5-18a)
1/(ms1cp1)1/(ms2cp2)1/(ms1cp1)-1/(ms2cp2)
dT
dt
dQ=
(5-19)
11
如前述,m为常数;又(dT-dt)=d(T-t),于是dQ=-d(T-t)/m,代入传热速率式令
m=
ms1cp1ms2Cp2
(5-13),得到
(5-20)
K(T-t)dA=_d(T-t)
或
K△tdA=-d(△t)/m[将总温差(T-t)写成△t]
m
分离变量,在A=0(x=0的热流体进口处的截面Ⅰ,△t=△t1=T1-t2)至A=A(x为换
148化工原理
【例5-6】有一列管换热器,由25mm×2.5mm的钢管组成。CO2在管内流过,准
应用式(5
却水在管外流过。已知管内的a1=50 W•m2K1,管外的α2=2500 W•m?•K1。(D
传热系数;(2)若设法使a1增大1倍,其他条件与前相同,求传热系数增大的百分
(3)若使a2增大1倍,其他条件不变,求传热系数增大的百分率;(4)若计算传热系
与本例(
时,不对内、外表面的差异做校正[采用式(5-11)],误差有多大?
从以
解(1)求以外表面积为基准时的传热系数根据附录四,取钢的热导率=
三、f
W·mK3;从表5-5中查CO2侧污垢热阻取R1=0.5×10-3m2•K·W-1,冷却水侧污
讨论
热阻按井水取R2=0.58×10-3m2·K·W-1,应用式(5-11c)有
的传热面和
+1
行积分。
+
a2
K2 and1
250.5×10-3×250.0025×25
45×22.5+0.58×10-3+
50×20
20
2500
=0.025+0.000625+0.000062+0.00058+0.0004
=0.02667m2K.W-1
K2=37.5W.m2.K-1
钢管壁的热阻占总热阻的比例为0.000062/0.02667=0.0023,可见工程计算中完全可以
忽略。
(2)a1增大1倍,即a1=100W·m-2K1时的传热系数K',式(5-11c)右边只有第
项减为一半
K7=0.0125+0.000625+0.000062+0.00058+0.0004=0.01417 m2KW
K'=70.6W.m2.K-1
K值增加的百分率=
K'-K2×100%=
70.6-37.5
K2
37.5×100%=88.3%(明显增大)
(3)a2增大1倍,即a2=5000W·m2·K1时的传热系数K"
考察
=0.025+0.000625+0.000062+0.00058+0.0002=0.0265 m2KW
t随距离
变化dT
K"=37.7W.m2K1
量相等
K值增加的百分率=K"-K
K×100%=37.7-37.5
37.52×100%=0.53%(几乎没有增大)。
(4)文中述及,当几个分热阻差别大时,总热阻与控制热阻相近。本例有控制热阻
式中,cp
1/a1,而K1≈a1。但现在a1系对管内,故先求得对管内表面的K1后,需再通过式(5
ms1、ms2
17)换算为对管外表面积的K2,才能进行比较。
取负号是
式(5-11)加上污垢热阻后应为
令
代入已知数据
如前述,
K0.02+0.0005+0.00056+0.00058+0.0004=0.02154
(5-13),
所以
K1=46.4W.m-2.K-1
或
分离变量
2)mhR
第五章传热151
(5-21)
【例5-7】在一列管式换热器中用机油和原油换热。机油在管内流动,进口温度为
N5℃,出口温度下降到175℃;原油在管外流动,温度由120℃升到160℃(1)试分
(5-22)
测计算并流和逆流时的平均温差;(2)若已知机油质量流量m=0.5 kg+e、定压比热
=3kJkgK,并流和逆流时的K均为100Wm3K,分别求所需的传热面积。
解(1)分别求(△tm)和(△tm),见表5-7。
5-22a)
表5-7
项目
逆流
(Arm)逆和(Arm)
T
245-175
19a)
160-120
并流
Ar
8555
245-*175
85-55
30
Mm
In(85/55)0.435
120-160
=68.9
12515
3
125-15110
In(125/15)2.12=51.9
(2)Q=ms1p1(T1-T2)=0. 5×3×(245-175)=105 kJ•s
247
A逆
Q
K(Atm)i105×1000
100×68.9=15.2m2
A并
=
Q
K(△tm)并105X1000=20.2m2
s2
100×51.9
3)
由本例可见,当两流体的进、出口温度都已确定时,逆流的平均温差比并流的大,因此
当
传递相同热流量时,逆流所需的传热面积比并流小。逆流的另一优点是可以节省冷却剂或加
与
热剂的用量。因为并流时,t2总是低于T2,而逆流时,t2却可以高于T2,所以逆流冷却时,冷却剂的温升(t2一t1)可比并流时大些,对于相同的热流量,冷却剂用量就可以少些,同理逆流加热时,加热剂本身温降(T1-T2)可比并流时大些,也就是说,加热剂的用量可以少些。但应当注意的是,上述两个优点不一定同时具备:若是利用逆流取代并流而节省了冷却剂或加热剂,则其平均传热温差就未必仍比并流时大。
【例5-8】某工厂用300kPa(绝)的饱和水蒸气,将环丁枫水溶液由105℃加热至115℃
后,送再生塔再生;已知其流量为200m3·h1、密度为1080kg·m3、比热容为2.93kJ·kg
K,试求蒸汽用量。又若换热器的管外表面积为110m2,求传热系数;计算温差时水溶液的
温度可近似取为其算术平均值。
解使冷流体由105℃加热至115℃所需的热流量为
200
Q=ms2cp2(t2-t1)=
×1080×2.93×(115-105)≈1760kW
3600
加热蒸汽放出的热流量与之相等Q=ms1r=1760kJ·s-1
压力为300 kPa(绝压)的饱和蒸汽,其对应的温度为133.6℃、汽化潜热为2164k·kg-10,故mi=1760
=0.813 kgs-1
2164
由饱和水蒸气的压力求其对应的温度及潜热,可查本书附录九;或根据本章附录关联式(5-113)至式(5-118),利用程序计算工具计算;通常以后者为便。两者的数值可能有差异,但不影响所得的最终结果,
152化工原理
应用式(5-23)求传热系数,其中平均温差为
105+115
=23.6℃
依次往返流过名
△m=133.6
2
为一程,图5-1
系数,但同时也
A1+(133.6-105)+(133.6-115)28.6+18.6
以上算法相当于用算术平均温差
2
=23.6℃
去部分布管面积
2
Am=
Q1760×103=678W.m2.K-1
敌
K=
A△t110×23.6
【例5-9】有一列管式换热器(见图5-15),其传热面积A=100m2,用作锅炉给水原油之间的换热。已知水的质量流量为550 kg·min1,进口温度为35℃,出口温度为75油的温度要求由150℃降到65℃,由计算得出水与油之间的传热系数K=250W·m2K问如果采用逆流操作,此换热器是否合用?
解所要求的传热速率Q可由热量衡算求得
参与热交
Q'=mcp2(t2-t1)=(550/60)×4.187×(75-35)=1535 kW
程),由另一
校核换热器是否合用,取决于冷、热流体间由传热速率方程求得的Q=KA是
安装一定数目
大于所要求的传热速率Q'。若QQ'则该换热器合用。或由Q'=KA'△rm得出要求的
使流体多次横
热面积A',若A'<A,则该换热器适用。
流向交错的流
已知K=250W·m2K1,现有的传热面积A=100m2
图5-17(
(150-75)-(65-35)45
图5-17(b)所
△tm
=
=49.1
75
℃
150-75
In65-35
In
沿一个平行的
30
图5-18
Q=KA△t=250×100×49.1≈1230000 W(或 1230 kW)
流),和流体
Q<Q,故该换热器不适用。要求的传热面积A=Q
1535000
示;也可以是
KAtm250×49.1=125m2(>A).
也可说明该换热器不适用。
T2=65℃
1
2=75℃
水
1=35℃
油T1=150℃
2
图5-15
四、复杂流向时的平均温差
例5-9附图
以上表明,就传热平均温差来说,逆流比并流优越。除非冷流体被加热的温度不得超过
图5-17
某一规定温度、或热流体被冷却的温度不得低于某一规定温度,因而采用并流较易控制或
有其他特殊要求外,一般应尽可能采用逆流操作。但在换热器的设计中,除温差的大小以
错流
外,还要考虑到影响传热系数的多种因素以及换热器结构等方面的问题。所以实际上单纯的
可以想
逆流或并流并不多见,而是采用比较复杂的流向。
如1-2折流
当管内流体的流速过低,使得传热速率过小时,为了提高管内流速,可在换热器顶盖内装
次往返流过各组管,最后由出口处流出,这种换热器称为多管程列管式换热器(流过一组管称一程,图5-16所示为2管程换热器)。采用多管程,虽然能提高管内流体的流速而增大其给热
第五章传热153
数,但同时也使其阻力损失增大,且平均温差会降低(达不到完全逆流)。此外,隔板也要占部分布管面积而使传热面积减小。因此,程数不宜过多,一般以2程、4程、6程为常见。
+折流挡板
+
户给水和
隔板
为75℃,
一
n-2·K-1,
图5-16有隔板和折流挡板的列管换热器示意
参与热交换的另一种流体则由壳体的接管进入,在壳体与管束间的空隙处流过(称为壳
是否
求的传
按装一定数目与管束垂直的折流挡板(见图5-16)。这样既可提高壳程流体流速,同时也迫流体多次横向流过管束,增大湍动程度。这时两流体间的流动是比较复杂的多程流动或是流向交错的流动。
图5-17(a)所示为参与换热的两流体在传热面两边的流动方向相互垂直,称为错流。图5-17(b)所示为其中一边流体反复地做折流,代表多管程内的流动;而另一边的流体只一个平行的方向流动,使两边流体间交替出现并流与逆流。这种情况称为简单折流。图5-18所示为简单折流中热流体做单程流动、冷流体做双程流动的组合(简称1-2折
流),和流体温度沿流动路程而变化的情况。两流体可以是先逆流后并流,如图5-18(a)所
A'),
示;也可以是先并流后逆流,如图5-18(b)所示。
12
7
2
2
T
11
2
T
(a)错流
T
T2
12
2
1
2
t1
SS+dSA
0
SS+dSA
(a)先逆流后并流
(b)先井流后逆流
(b)简单折流
图5-181-2折流时的温度变化
过
图5-171、2两流体成
错流和折流的示意
或
以
可以想象,在上述复杂流程中,平均温差△m的计算远比单纯并流或逆流时复杂。例
的
如1-2折流时理论导出的平均温差计算式如下
√(T1-T2)2+(t2-1)2
(5-25)
Atm
(T1-t2)+(T2-1)+√(T1-T2)2+(t2-1)
In
/
(T1-t2)+(T2-t1)-√(T1-T2)2+(t2-t1)2
P月样校正系数中→
s校正系数中
→156
0校正系数中
→
0100
000校正系数中
=→
河
3R0
0十一10
-↓020
2
2
、-↓
-↓
0S0600
盒100
昆00
0
-0老08
2000
0一
心
年年
总传执手数为常数:AQ
t2-t1
PT-t1两流体的最初温差
冷流体的温升
第五章传热155
代表传热
R=
T1-T2热流体的温降
t2-t1
P、R的具体关系可对不同况由理论导出,现以1-2折流为例
冷流体的温升
Atm
=m.逆
(T1-t2)-(T2-t1)
△tm,逆In[(T1-t2)/(T2-t1)]In[(1-P)/(1-PR)]
(5-35a)
而式(5-25)用P、R表示时,为
(R-1)(t2-t1)
(5-26)
(5-36)
(5-27)
Atm=
√R2+1(t2-t1)
In2-P(1+R-√R2+1)
2-P(1+R+√R2+1)
(5-25a)
(5-28)
将式(5-25a)及式(5-36)代入式(5-35a),得
√R2+111-P
(5-29)
4=
R-11-PRIn2-P(1+R-√R2+1)
L2-P(1+R+√R2+1)
(5-37)
一较复杂的=(P,R)函数关系,可在计算后绘成图5-19(a),以便于查用。
(5-30)
对于单壳程、管程为4、6、8等偶数时的复杂折流换热器,可近似作为1-2换热器处理,即亦可应用图5-19(a)。图5-19(b)所示为2壳程,管程为4,8,…时的φ=φ(P,R)
5-31)
关系;图5-19(c)所示为1-3折流,代表1壳程3(奇数)管程的情况;图5-19(d)所示为错流时的情况。
由图可知≤1,即△tm≤△tm,逆,这是由于复杂流动中同时存在逆流和并流。在设计时
-32)
应注意使≥0.9,至少不应低于0.8;否则经济上不合理,而且若操作温度稍有变动(P稍增大),将会使值急剧下降,即缺乏必要的操作稳定性。增大的一个方法是改用多壳程,即将几台换热器串联使用[对比图5-19(a)与(b)]。
33)
【例5-10】在一1-2换热器中,用水冷却异丙苯溶液。冷却水走管程,温度由20℃升至0℃,异丙苯溶液由65℃冷至50℃。求平均温差。
解T1=65℃,T2=50℃;t1=20℃,t2=40℃
对于逆流
△t1=T2-t1=50-20=30℃
△t=T1-t2=65-40=25℃
4)
30+25
△tm,逆2=27.5℃
用
T1-T265-50
R=
=0.75
t2-t140-20
t2-t140-20=0.44
P=T1-t165-20
查图5-19(a),得=0.93,故有
△tm=△tm,逆=0.93×27.5=25.6℃
五、传热效率-传热单元数法
以上传热计算的基础是下述两关系,共三个方程。即
热量衡算方程
154化工原理
此式对图5-18中的两种1-2折流情况皆可适用。
现以图5-18(a)所示的1-2换热器为例,说明理论推导△m计算式的思路。图中垂线T/tS代表
选学内容
面积为S时的情况,流体温度T、t'及t都是S的函数。
对图中TS线右侧的热量衡算为
mstcpt(T1-T)=mcp(t-t+t-t)
φ与P,R的
=ms2cp2(t'-t)
对微元面积dS的热量衡算为
-=(dt'-dr)
其中
而式(5-25)
第一管程在dS段的传热速率方程为
=K(T-1ds
(50)
第二管程在dS段的传热速率方程为:-ms2cp2dt'=K(T-t')dS
(5-)
将式(5-25a)
将式(5-27)、式(5-28)代人式(5-26),得
msicp dT
KdS
=2T-t-t
(5-2)
为消去式(5-29)右侧的t'与t,先将该式对S微分
此一较复杂
msicpi d2To dT dt dt'
对于单
K ds2 ds ds ds
(5
理,即亦可
然后借助式(5-27)、式(5-28)及式(5-26),将式(5-30)改换成下列形式
d2t_2k dT(K
关系;图5-
ds2 msicp1 dsms2c(T1-T)=0
(5-3
错流时的情
此式是一个二阶线性常微分方程,代表热流体温度沿流程的变化。其边界条件为
由图可
S=0,T=T2(及t=t1、t'=t2);
应注意使
S=A,T=T1(A为一个管程的传热面积)
(5-32)
增大),将会
此微分方程不难解出,其结果为
即将几台换
T1-T=(T1-T2)exp(m1A+m2 S)-exp(m2A+m1 S)
式中,m1、m2为下述特征方程的两个解
exp(m1A)-exp(m2A)
(5-33)
【例5
升至40℃
m2-2K-(m)=0
解
ms1cpl
由传热速率方程K(2A)△tm=ms1cp1(T1-T2)知
对于
△tm=(T-t2)
可见,为求得△m需先将mcp1/2KA化成温度间的关系。为此,先将式(5-33)对S求导,再应用
2KA
(5-30
式(5-29)及S=0时的边界条件,通过代数运算,即可得到式(5-25)。
对于常用的复杂折流或错流的换热器,也可用理论推导求得其平均温度差的计算式,形式将更为复杂。
通常采用一种比较简便的计算办法,即先求两边流体假定为逆流情况的对数平均温
查图5-19
△m,逆再根据实际流动情况乘以温差校正系数而得到实际平均温差△m
△tm=p△t
五、
校正系数则表达成以下P、R两参数的函数,可查图而得到=(P,R)。
m,逆
以上
热量衡算
传热速率方程一
Q=(T-T2)=
Q=KA△tm
第五章传热157
三个方程中除定压比热容cp、Cp2随温度的变化小,可由手册查出作为已知量外,还有9个变量:ms、m2、T1、T2、1、2、K、A和Q。其中需给出6个,才能进行计算。若给定
(5-22)
量中包括流体在进、出口的4个温度、就可以直接应用式(5-22)两个方程。如例5-7中因
(5-23)
、2、、2、K、m已知△m易于算出Q、m、A随之而定,这类问题通常在设计时出现,而称为设计型问题。
传热计算的另一类问题是给定m1、m2、K、A和两个温度如T1、1,求解其他两个温度T2、t2及Q。这类问题通常在改变操作条件或核算时出现,而称为操作型问题。在求解时,由于冷、热流体各有一个温度未知,加之Q也是未知量,故无法由热量衡算式(5-22)解出两个未知温度;同时两个未知温度还出现在式(5-23)的对数项中,故对式(5-23)及式(5-22)联立求解时需采用试差算法。对此,较方便的是采用另一种方法,即传热效率传热单元数法,简称-NTU法。而前述三方程联立求解的方法称为对数平均温度差法,简称LMTD法。它不便于求解操作型问题。
(一)传热效率
换热器传热效率的定义为实际传热速率Q和理论上可能的最大传热速率Q之比
Q
(5-38)
首先讨论一下Q的确定。不论在哪一种形式的换热器中,根据热力学第二定律,热流体至多能从进口温度T被冷却到冷流体的进口温度1,而冷流体的出口温度t2不可能超过1,即在换热器中两种流体可能达到的最大温差均为(T1一t1),因而
Qmax=(mscp)min(T1-t1)
(5-39)
式(5-39)中的mcp应是两流体中热容流量数值较小的一个,这是由于:从热量衡算式(5-22)得知,热流体放出的热量等于冷流体得到的热量;若计算Q时以mc较大的流体为准,则另一流体的温差必然大于最大值的(T1一t1),而这在热力学上是不可能的。若热流体的m2c较小,则令ms1cp1=(mscp)min,于是
Q(T1-T2)T1-T2
Qmax ms1cp1(T1-t1) T1-ti
这时m2cp2用(mcp)max表示,反之,冷流体的热容流量mcp较小时,则(mcp)min=m,2C2,此时m1cp1用(mcp)max表示,则有
Qms2cp2(t2-t1)t2-t1
EQmax ms2cp2(T1-t1) T1-t1
若能知传热效率ε,则由Q=Qmax=e(mcp)min(T1-t1)求得Q后,便很容易从热量衡算求得两个出口温度T2和2。这样,问题就集中到如何求出传热效率,为此先引入传热单元数的概念。
(二)传热单元数
在换热器中,对微元传热面dA的热量衡算和传热速率方程为
dQ=ms1Cp1dT=ms2Cp2dt
=K(T-t)dA
对于热流体,上式可改写为
dtKdA
T-1msiCpl
其积分式称为对热流体而言的传热单元数,用NTU表示
158化工原理
当K为常数及推动力(T一t)用平均推动力△tm表示时,则积分式简化为
T1-T2 KA
NTU1=
式中,C
Atm
ms1cp1
(5-40)
不同情况
传热单元数的概念是由努塞尔首先提出的。其中,(T1一T2)为热流体温度的变分别表示
m为热、冷流体间的平均温度差。故对热流体的传热单元数可看成是热流体温度的变化
CR,可
当于平均温度差的多少倍。
型问题则
对式(5-40)的第二个等式,可改写为:
流间的差
A=NTU1(ms1cp1/K)
(5-40a)
可知式中的msicp1/K为一个传热单元(NTU1=1)的传热面积,称为传热单元面积;而
个换热器的传热面积A,为此单元面积与传热单元数之积。
同理,对于冷流体
NTU下_6
KA
ms2Cp2
(5-41)
(三)传热效率e和传热单元数NTU的关系
对于一定型式的换热器,传热效率和传热单元数的关系可以根据热量衡算和速率方
导出。现以逆流换热器为例,应用式(5-19)将式(5-21)改写为
-m)
设热流体的热容流量较小,即(mcp)min=ms1Cp1,将上式写成
(5-21a)
将式(5-40)代人,并令ms1cp1/ms2cp2=CR1(CR1≤1),得
T1-t2=NTU1(1-CR1)
1.0
In T2-ti
为了找出e与NTU1的关系,进行下列转换
(5-21b)
0.8
T2-t1=T1-t1-T1+T2=(T1-t1)-T1-t1
T1-T2(T1-t1)=(1-e)(T1-t1)
0.6
T1-t2=T1-t1+t1-t2=(T1-t1)-t2-t1T1-T2(T1-t1)
T1-T2^T1-t1
0.4
=(1-sile)(T1-t1)=(1-CRie)(T1-t1)
ms2cp2
将上述转换关系代入式(5-21b),并解出e,得
0.2
1-exp[NTU1(1-CR1)]
ECR1-exp[NTU1(1-CR1)]
0
若冷流体的热容流量较小,则将式(5-21a)写成
(5-42)
T-12-KAms2cp2-1)
图
In T2-t1
将式(5-41)代人,并令m2cp2/msicp1=CR2(=1/CR1,CR2≤1),同样可解得
(5-21c)
1-exp[NTU2(1-CR2)]
当m
E=CR2-exp[NTU2(1-CR2)]
式(5-43)与式(5-42)的结构相同,可写成统一的形式
Cp2,则C
(5-43)
同理
1-exp [NTU(1-CR)]
eCR-exp[NTU(1-CR)]
第五章传热159
(5-40)
式中,CR为热容流量比,CR=(mcp)min/(macp)mat s
(5-44)
度的变化,
的变化相
不同情况下与NTU、CR的关系已作出计算,并绘制成图。供计算时选用。图5-20~图5-22
分别表示并流、逆流、1-2折流时的e=e(NTU,CR)关系。在操作型问题中已知NTU及(,可从图中查得e,从而可不经试算即可求出其他两个未知温度(见例5-11)。但对设计
(5-40a)
流间的差距,看是否应修改设计,而用eNTU法则不能做到这一点。
1.0
积;而整
CR=0
0.8
0.250.50
(5-41)
▲0.6
0.75
0.4
1.00
方程式
A.(T-另=
0.2
血
TK=常数
5-21a)
零
t2
1.02.03.04.05.0
NTU
图5-20单程并流换热器中e与NTU和CR之间的关系
1.0
0.25
1.0
CR=0
21b)
0.50
0.25
0.8CR=0
0.75
0.8
0.50
1.00
0.75
0.6
0.6
1.00
0
0.4
0.4
T1K=常数
K=常数
0.2
0.2
12
T
T2
1
12←
I
T2
0
0
1.02.03.04.05.0
1.02.03.04.05.0
NTU
2)
NTU
图5-221-2折流换热器中e与NTU
图5-21单程逆流换热器中ε与NTU
和CR之间的关系
和CR之间的关系
c)
当micp<mecpe,有CR=CR1,NTU=NTU1,e=(T1-T2)/(T1一1);而若 macp1>me,则CR=CR2,NTU=NTU2,e=(t2-t1)/(T1-t1)。
同理,对并流换热器可导得与NTU的关系为
1-exp[-NTU(1+CR)]
(5-45)
=
1+CR
162化工原理
(3)传热量
Q=K2A2△t2=231×296.2A2=68420A2
传热机理
表5-8
(4)管内壁温度T及管外壁温度t
T=T-Q/1A1,T为热流体温度,取进、出口温度的平均值,即T=(575+472)/2=
相差甚远
有益处。
523.5℃,代入式中得
68420A
T=523.5℃-
=238.4℃
300A
给
空气自然
管外壁温度
气体强制
68420A2
bQ
0.0025
=238.4-
×
水的自然
I =TwAAm
45
Am
水的强制
0.002568420×25
=238.4-
×
=234.2℃
45
22.5
二、
由此可见,由于水沸腾一侧的给热系数比另一侧的大得多,故内壁温度接近于水的
(一)
度(227.3℃)。同时,由于管壁的热阻也很小,故管外壁温度与内壁温度相差不大
研究
远低于转化气的平均温度(523.5℃)。
计算式。
式,它并
第四节给热系数
要途径。
(1)
以上介绍了传热速率方程[式(5-23):Q=KA△t],在不同情况下平均温差△tm的求
简化条件
取,以及在热、冷流体的4个终端温度T1、T2、t1、t2中有两个为未知时,避免试差的
然后获得
热问题的
解法。其中传热系数K按式(5-11):K=(++)
分析解。
式(5-11c)]计算。本节讨论这些公式中给热系数α1、a2的求取。
及其修正式[式(5-11a)~
若上
一、给热系数的影响因素和数值范围
余年来,
影响给热的因素很多,总体而言,这些影响因素可以分为以下几方面。
内的燃烧
(1)引起对流的原因可分为强制对流和自然对流两大类。流体因用泵、风机输送或
(2)
搅拌等外力作用产生流动时,称为强制对流。由于流体内部存在温差,使各部分流体的密
关联式或
发生差异而引起的流动,称为自然对流,所导致的传热称为自然对流给热。这两类对流给热
通用性,
的流动成因不同,所遵从的规律也不同。通常强制对流的湍动较为强烈,故其给热系数也较
纲分析法
大。有时两种对流都需要考虑,这种情况则称为混合对流给热。
关系。这
(2)流体的流动形态图5-12描述的是湍流情况。对于层流,传热需依靠热阻大的导
热;只有自然对流会附加一些传热方向上(垂直于壁面)的质点运动而增大传热速率。总的
绍其量纲
来说,层流时的给热系数明显比湍流时小。
(二)
(3)流体的物理性质前已提及,雷诺数Re的大小影响膜厚,而Re中含有流体的
根据前
度、密度。还有热导率则直接影响膜的传热性能。对于自然对流给热,体膨胀系数的大小会
尺寸l、流
影响对流的强弱。另有其他一些物性将在涉及时提到。
函数式表示
(4)传热面的几何因素传热表面的形状、大小、流体与传热面作相对运动的方向以及
传热面的表面状况也是影响给热的重要因素。还可将流体的流动分为内部流动(如圆管内、
这7
套管环隙中的强制对流)和外部流动(如圆管外或管束间的强制对流)两类。
无量纲特
(5)流体有无相态变化前述的情况都是流体作单相流动,依靠流体的显热变化实现给
个无量纲物
热;而在有相变的对流传热过程中(现指沸腾或冷凝),流体的流动状况有了新的特点,其
丌1、丌
(1)多
【例5-12】质量流量、温度等数据同例5-11,又假定K值也不变,若换热器改为并流操作,求所需传热面积。
第五章传热161
的中间温
前者整理
和度与511C0.5=0.
流的图5-20得NTU=0.75,故有:
A=
R与R、
NTUXms1cp10. 75×2.5×1.0×103
K
由此可见,在流体进、出口温度相同时,并流所需的传热面积比逆流时大,这再次说
80
=23.4m2
明前面并流与逆流对比的结论。比较图5-20和图5-21也可以看出,在传热单元数相同
(5-46)
定经济上合理的NTU值。
六、壁温的计算
在后面讲到的热损失计算以及某些给热系数的计算中,都需要知道壁温。此外,选择换
热器的类型和换热管材料时,也需知道壁温
5-46a)
对于稳定传热过程
之处。
Q-aA(T-T)-Am(T-1)
=aA(tn-t)=KA△tm
进行
系数
式中,A、A2、Am分别代表热流体侧传热面积、冷流体侧传热面积和平均传热面积;
,1分别代表热流体侧和冷流体侧的壁温;,分别代表热流体侧和冷流体侧的给
定压
热系数。
整理上式可得
去
T
Tw=TQ
anAn
十tunt
(5-47)
tw=TwbQ
AAm
壁温Tt值接近小值较大
(5-48)
或
tw=t+Q
热阻较一侧的流体温度
(5-47a)
aAc
【例5-13】有一废热锅炉,由25mm×2.5mm锅炉钢管组成。管外为沸腾的水,压
力为2.57MPa。管内走合成转化气,温度由575℃下降到472℃。已知转化气一侧a=
300 W•m2•K1,水侧 α2 =10000 W•m2K1。若忽略污垢热阻,试求平均壁温 T及。解(1)传热系数以管外表面A2(冷流体侧)为基准
bd21dz
=0.0001+0.000062+0.004167
=0.00433
K2=231W.m2.K-1
(2)平均温度差水在2.57MPa即绝压2.67MPa下的饱和温度为227.3℃,有
(575-227.3)+(472-227.3)_347.7+244.7=296.2
2
△tm=
2
160对于一组串联的换热器,其传热单元数为各换热器之和
化工原理
K1A1+K2A2+K3A3+…
【例5-
NTU=
(mscp)min
流操作,求
易于得到其传热效率,从而得到总的温升及温降;比LMTD法要试算各换热器间的中间
解由
流的图5-2
从以上eNTU法的导出过程,可知其与LMTD法都是基于同一个来源,只是前者整理度要方便很多。
成e、NTU及CR之间的关系,而后者整理成为、P及R之间的关系。实际上,CR与R
由此可
与P还具有以下的对应关系。
当冷流体的热容流量较小,有
明前面并流
ms2Cp2-T1 -12-RI
时,逆流换
CR-msicp1 t2-t1
而增加,但
t2-t1=P
(5-46)
定经济上合
eT-t1
六、壁
当热流体的热容流量较小,有
在后面
CR=ms1cpl=T.-Ta=R
ms2cp2
热器的类型
T1-T2
=PR
(5-46a)
对于稳
e-T-t1
比较可知两法并没有实质性的差别,只是对于不同类型的问题,在应用上各有其方便之处【例5-11】空气质量流量为 2.5kg·s1,温度为100℃,在常压下通过单程换热器进行冷却。冷却水的质量流量为2.4kgs2,进口温度15℃,与空气作逆流流动。已知传热系数
式中,AB、
K=80Wm2K1,又传热面积A=20m2,求空气出口温度和冷却水出口温度。空气的定压
TB,tw分别
比热容取为1.0kJ·kgK1,水的定压比热容取4.187kJ·kg-1K-1
热系数。
解此为两流体出口温度未知的情况,不便于用LMTD法求解,以下用e-NTU法
整理上式可
水的热容流量
空气的热容流量
ms2cp2=2.4×4.187=10.05 kW.K-1
ms1Cp1<ms2cp2,故取
msicp1=2.5×1.0=2.5 kW.K-1
(mscp)min=ms1cp1=2.5 kW.K-1
或
(mscp)max=ms2Cp2=10. 05 kW.K-1
NTU=KA80×20
【例5-1
msicp1 2.5×103=0.64
力为2.57M
CR=
msicp12.5
300 Wm2.
根据NTU=0.64和CR=0.25,由逆流换热器的图5-21查得ε=0.48。空气出口温
ms2cp210.05=0.25
度T2可根据传热效率的定义求得
解(1
T1-T2100-T2
TI-t1100-15=0.48
冷却水出口温度t2可由热量衡算求得
T2=100-85×0.48=59.2℃
Q=2.4×4.187(t2-15)=2.5×1.0×(100-59.2)=102 kW
102
t2=2.4×4.187
+15=25.2℃
(2)平
热机理也不相同;还有相变潜热起重要作用
第五章传热163
有益处。
表5-8给出了几种常见情况下给热系数的大致范围。由表可知,不同情况下的给热系数
给热情况
表5-8
空气自然对流
给热系数/W·m2K-1
给热系数的大致范围
气体强制对流
5~25
给热情况
水的自然对流
20~100
油类的强制对流
给热系数/W·m2K-1
水的强制对流
200~1000
水蒸气的冷凝
50~1500
1000~15000
有机蒸气的冷凝
5000~15000
水的沸腾
500~2000
二、给热系数与量纲分析
2500~25000
(一)获得给热系数的方法
温
而
研究给热的主要目的是要揭示其主要影响因素及其内在联系,并得出给热系数a的具体针算式。给热现象相当复杂,影响a的因素很多,牛顿冷却公式只能看作是a的一个定义,它并没有涉及有关因素与a的内在联系。目前,获得a表达式的方法可分为以下两种主要途径。
(1)数理演绎法指对某一类给热问题,根据流体流动及热量传递的一般规律,在一定
求
简化条件下建立起偏微分方程及其定解条件;求得分析解后,得出其温度场和壁面热通量,然后获得给热系数。这种方法能较深刻地揭示有关物理量对给热速率的影响程度,是研究给热问题的基础理论方法。然而,由于数学上的困难,目前只能得到个别简单给热问题的理论分析解。这方面的内容较为深入,在传热学或化工传递过程的专著中有论述。
若上述数学描述不能得到分析解,可对其离散化,用数值法求解而得到给热系数。二十余年来,这种方法得到了迅速发展。很多工程问题需借助这种方法才能进行分析,如气化炉内的燃烧等复杂的给热问题。
(2)实验归纳法对不同的给热问题进行实验,将实验数据归纳成给热计算式(常称为关联式或经验式),仍然是目前工程计算的主要依据。为减少实验工作量,提高实验结果的通用性,应当在量纲分析的指导下进行;即对某一类给热问题,将影响给热系数的因素用量纲分析法得出几个无量纲的特征数,以减少变量数目,再用实验确定这些特征数之间的具体关系。这种方法在求取管内湍流的摩擦损失中已经用过。以下再对没有相变的给热问题,介绍其量纲分析。
(二)强制湍流时的特征数方程
根据前述影响给热因素的分析,得知此情况下的给热系数a主要取决于传热设备的定型尺寸1、流体的流速u、黏度μ、热导率、定压比热容cp、密度p。这7个物理量可用普遍函数式表示为
f(l,u,μ,A,cp,p,a)=0
(5-49)
这7个物理量涉及四个基本量纲,即长度L、质量M、时间T和温度。按照定理,无量纲特征数的数目等于变量数n与基本量纲数m之差,即为n-m=7-4=3个。令这三个无量纲特征数为π1、π2、π3,则式(5-49)可转换成
(5-50)
(π1,π2,π3)=0
1、π2、π3可采用第一章所述的量纲分析法得出,现分别解释如下。
(1)努塞尔(Nusselt)数 π1=Nu=al/λ。其中含待求的a,是特征数方程中的待定
数。其意义为:将 Nn改写成Nu=α△t/△t/1)[△t为给热温差],可知Nu代表给热速
164化工原理
与流体层厚度为1的导热速率之比;又若应用当量膜厚8'的概念(见图5-12),有a=
于是Nn=(A/8′)1/A=1/8',即设备定型尺寸1与当量膜厚δ′之比。
按照公理2
(2)雷诺数2=Re=lup/μ。已在第一章第三节中阐明是惯性力与黏性力之比。
式中,a1,j为待定
(3)普朗特(Prandtl)数 π3=Pr=cpμ/A。代表流体物性对给热过程的影响。
由式(5-54a)、式
将此式及式
选学内容
(三)量纲分析定理的证明
这里对第一章求特征数的定理作出普遍性的证明,并导出求无量纲参数(无量纲数群)的新方
按照公理3,其
在变量数目较多时,应用此法较为方便。
1.定理的证明与无量纲数群的导出
则
将描述某物理现象的普遍函数式(指物理量间的关系式)写成
代入式(5-56),
f(a1,a2,…,ak,bk+1,…,bn)=0
(5-51)
式中,包含n个有量纲的量,选定k个量(a1,…,ak)作为独立变量,其中应包括该现象所》的全部基本量纲,故k一般即为基本量纲数;其余(n一k)个则称为“依赖量”,其量纲可由独立
量量纲的幂次组合得到。例如等加速度运动物体所走距离的算式
令1
=b+1
l=u0+(1/2)a02
于是
共有四个变量1、、0、a,其量纲分别为:[]=L、[u]=LT1、[0]=T、[a]=LT-2。本例k=2(
式中,前k
L及时间T),可以任选两个量作为独立变量a1、a2,其余两量b3、b4的量纲可由a1、a2导得。例如的,即为无量
a1=1、a2=u,则[b3]=[O]=[l/u]=T、[b4]=[a]=[u2l]=LT-2。
特征数,可根据
白金汉的定理表明:可将任一物理方程转换成无量纲的方程;无量纲数群为物理量数n减基本量
2.强制对
数k之差。即式(5-51)可转变成
前已得知此
F(π1,π2,…,πn-k)=0
为证明定理,除上述量纲一致的原则以外,还需应用以下关于量纲和单位的三条公理。
(5-52)
7个变量的
①物理量A的大小等于其度量单位(A)与一数值a之积。例如某一长度A=3.2m,意为A是期量单位m的3.2倍,这里a=3.2,(A)=m,A=a(A}。
②物理量A与度量单位(A}的大小无关。例如对于某一长度,以米为度量单位可知为3.2m,如
本现象可
厘米为度量单位,则应为320cm,虽然用不同的单位所得数值不同,但长度并未改变,即与度量单位的大小无关。
因其中未包括
③物理方程的函数形式与所采用的度量单位无关。即无论是用SI制、c.g.s制、英美制或其他单位
对式(5-49
制,函数形式不变。以前各物理方程适用于不同的单位制中,这一公理也都得到体现。
量纲形式而采
若式(5-51)中n个量的数值是用k个独立变量的度量单位(简称独立单位){A1},(A2},…,(A)得出,现将各独立单位分别缩小为原来的1/c1+1/2,…1/ck,即改成(A1/c1)…,{Ak/ck),使式(5-51)转换为
为将此式转换
式中
f(a1,a,,ak,be+,,bn)=0
a1,…,a,b2+1,…,bn——改用新度量单位后各物理量的值。
(5-51a)
由公理1及公理2,物理量A1=a1{A1}=a1{A1/c1}可知
推广为
a1=a1ci
以下求依赖量B+1,…,B的新值b+1,…,b。按照公理1
a1=a1c(i=1,2,…,k)
(5-53)
代人式(5-56a)
面度量单位(B)可用独立单位的幂次组合表示如下。
B,=b1(B1)(j=k+1,…,n)
或
(5-54)
式中
代人到式(5-54)得
(B1}={A1}°1(A2}2,…,{Ak},=IⅡ(A)
以上得出
B=b)Ⅱ(A.)%
(5-54a)
普朗特数,用
热速率
=/’,
按照公理2
B,=b
第五章传热165
中,为待定指数,i=1,…,kj=k+1、…
由式(5-54n)、式(5-55)得
(5-55)
将此式及式(5-53)
代入式(5-51a)
b'1=b1
i
f(a1c1,…,act,bk+1C=1
方法,
好照公理3,其中,c1,…,c可以任意选择而不改变函数的形式,现按如下取值。
(5-56)
c1=1/a1,c2=1/a2,…,ck=1/a
则
代人式(5-56),得
=1/
-51)
涉及
f(1sb//)-
立变
=b+/a,…=ba/a
(5-57)
于是
f(1,…,1,π1,…,πn-k)=0
长度
选
式中,前k个量都已转换为1,无量纲。按量纲一致的原则,m1~共(n-k)个数群也应是无量纲
(5-57a)
的,即为无量纲数群。式(5-57a)可简化成式(5-52),这样就证明了#定理。至于如何求得各无量纲数群或
特征数,可根据上述原则简化手续,具体见下述实例。
纲
2.强制对流(无相变)时特征数的导出
前已得知此时的普遍函数式为
2)
f(l,u,p,,cp,p,a)=0
7个变量的量纲分别由基本量纲L、T、M、Θ如下组成:
(5-49)
度
[]=L,[u]=LT-1,[]=ML-1T-1,[]=MLT-30-1,
[cp]=L2T-20-1,[p]=ML-3,[a]=MT-30-1
本现象可选择1、u、μ、λ作为独立变量,它们包括了以上四个基本量纲,若选择、u、μ、p
就不当,
因其中未包括基本量纲Θ。
对式(5-49)中的物理量选用SI单位,即长度m、时间s、质量kg及温度K。为使式(5-49)转换为无
量纲形式而采取新的度量单位m/c1、s/c2、kg/c3、K/c4,将式(5-49)转换为式(5-56)的形式
f(lc1,ucic21,μe3e1 1c2 1,Ae3c1c2 3c41,cpeic22c41spec13,acac4e23)=0
(5-56a)
为将此式转换成式(5-57)的无量纲形式,对c1、c2、c3、c4如下取值
lc1=1,c1=1/1
ucic21=1,c2=uc1=u/l
μcc1c21=1,c3=cic2/μ=u/μl2
Ac3cicz3c41=1,c4=Ac3cic23=A/μu2
代人式(5-56a)中,即得到无量纲函数式f(1,1,1,1,π1,π2,π3)=0
(5-58)
或
中(π1,π2,π3)=0
式中
m1==a()(Hu /)(u)
π2=pc3c13=p(u/pl2)l3=lup/p
==Cpl-2(I u )(/)=/
以上得出的无量纲数群al/λ称为努塞尔数,用Nu表示;lup/μ即为雷诺数,用Re表示;cu/λ称为
普朗特数,用Pr表示。
流体密度不
系式可以简化为用幂函数表示
浮力(p1-
表示
Nu=CRemPrn
第五章传热167
(5-59)
=7-4=3
系数C与指数m和n由实验加以确定。其步骤是:先固定一个独立变量,求出Nu和
另一个独立变量之间的关系。例如舍伍德等用不同的流体,在Re=104时作管内流动的给
(5-61)
(5-59a)
热实验而得出图5-23。图中Nu和Pr是在双对数坐标上标绘的。不同Pr的流体的实验点,
都落在一条直线的附近,说明Nu与Pr之间的关系,在双对数坐标上可以用直线方程来表
示,即
或
lgNu=nlgPr+lgC'
Nu=C'Prn
400
(5-62)
(5-62a)
200
100
B
40
A
(5-60)
20
10l
0.61.0.24
102040
Pr
100200
图5-23Re=104时不同Pr的流体的实验结果
·空气;▲水;丙酮;×苯;煤油;正丁醇;1石油
与式(5-61)比较,应得C'=CRem,而指数n即为图5-23所示直线的斜率。按图中的A、B两点,可得
lg200-lg40
n=1g62-lg1.15≈0.4
再以lg(Nu/Pr4)为纵坐标,Re为横坐标,用不同Pr的流体在不同Re下的实验数据,
得到如图5-24所示的结果,并可用下列方程式表示
强制
103
下
102
2×1010
103
5×105
Re
图5-24管内强制湍流传热的实验结果
参阅 Sherwood: IEC, 24.736-745,1932。图5-23是经简化的示意图。文献作者采用丙酮、苯、正丁醇、水和煤油进行实验。原文中未考虑加热和冷却的差异。
166
化工原理
前面介绍自然对流给热时,曾指出它是由于流体内部存在温差,使得各部分流体密度
(四)自然对流时的特征数方程
系式可
同而引起的流动;故速度不是自变量。引起流动的推动力用单位体积流体的升浮力(、p)g=pgB△t表示,其量纲为ML-2T-2。因此自然对流给热可用下列函数关系式表示
系
f(a,l,p,p,cp,λ,pgB△t)=0
(5-59)另一个
式中包含7个物理量,4个基本量纲,按照π定理,无量纲数群的数目应为n-m=7-{热实验
都落在
个。可用下述特征数的关系式来描述该物理现象
(丌1,2,3)=0
示,即
(5—59a)
采用量纲分析方法导出π1,π2,π3。得
1 al-Nu
或
π2=l3p2gB△t/μ2=Gr
Gr为格拉晓夫(Glashof)数,代表升浮力的影响,相当于强制湍流的雷诺数
π3==Pr
于是描述自然对流给热的特征数普遍式为
Nu=f(Pr,Gr)
(5-60)
式(5-58)及式(5-60)中共含有4个特征数,见表5-9。
表/5-9特征数的符号和意义
特征数名称
符号
涵义
努塞尔数
N
待定特征数,包含待定的给热系数
与式(
雷诺数
Re-lup
μ
反映流体的流动形态和湍动程度
两点,
普朗特数
PG
反映与传热有关的流体物性
格拉晓夫数
Gr=l3p2βg△t
再以
μ2
反映由于温差而引起的自然对流的强度
得到
式(5-58)及式(5-60)表明,对于一定的传热面和流动情况,当Re和Pr确定后,强
对流时的Nu就被决定;当Pr和Gr确定后,自然对流时的Nu也就被决定。对不同情况下
的给热,其具体关系则需通过实验建立。在实验关联及其应用时应当注意以下几点。(1)定型尺寸Nu、Re中的l应如何选定。
(2)定性温度各特征数中的物理性质应按什么温度确定。
(3)适用范围例如强制对流时,Re和Pr各在什么范围内适用。
以下加上有相变的给热,共分四种情况来讨论给热系数的关联式,即
①强制对流时的给热系数;
②自然对流时的给热系数;
③蒸气冷凝时的给热系数;
④液体沸腾时的给热系数。
三、流体作强制对流时的给热系数
(一)流体在管内作强制对流
1.流体在圆形直管内作强制湍流
面已能明。此对热系数的特征散关联式为Na一fPr-Re)。在一定向。
煤油
168化工原理
p.-mlgRe+1gC
Nu
值。由于求壁
式中,m为图5-24所示直线的斜率;lgC为直线在纵坐标上的截距。
lg
1.05,冷却时
这样,n、m和C都可由实验数据求得。此外,为从实验数据得出特征数方程中待定的
【例5-14
指数和系数,也可以应用最小二乘法,它还能避免上述作图法可能引入的人为误差而提高准
到220℃,平
解在(
确度。
以下介绍此情况下应用最广泛的经验式。
0.0393W.m
当Re>10000,Pr=0.6~160,管长和管径之比l/d>50时,对管壁温度和流体平均
度相差不大的情况(所谓温差不大,其数值概念取决于流体黏度随温度变化的大小而定:
而
水而言,一般与壁面温差不超过20~30℃,对黏度随温度变化很大的油类则不超过10℃
Re>10000,
可采用下式计算
Nu=0.023Re0.8 Prn
(5-63
即
d -o e
对空气
(5-633)
其中,定型尺寸规定为管内径d。定性温度为流体进、出口温度的算术平均值。
结果相近。
当液体被加热时,n=0.4;当流体被冷却时,n=0.3。这一差别主要是由温度对层
2.流体在
底层中液体黏度的影响所引起的。对于主体温度相同的同一种液体,被加热时,它在邻近
流体在圆
壁处的温度较高,黏度较小,因而层流底层较薄而给热系数a较大;相反,当液体被冷部的方式进行。
时,它在壁面附近的温度较低,黏度较大,层流底层较厚,使a较小。至于气体,Pr中的
只有在管径小
黏度和热导率皆随温度升高而增加,结果气体的Pr基本上不随温度而变化;n取为04
这种情况,文
对于空气或其他对称双原子气体,Pr≈0.7。式(5-63)可简化为
Nu=0.02Re0.8
(5-63b)
对于短管,由于管入口处的扰动较大,a也较大;当l/d<50时,需要考虑短管效应
式(5-65)适
对式(5-63)算出的a乘以大于1的校正系数f1;f1取决于/d及Re,如图5-25所示
自然对流给
2.0
式中,除μw
径。在换热
3.圆形
1.0
当Re
0.51.0
0
1030
lld
100
的式(5-63)
图5-25管长的校正系数f
1-Re=104;2-Re=2×104;
4.弯曲
3-Re=5×104;4-Re=105;5-Re=106
流体在
当壁温与流体主体温度间的温差较大,超出前面所述的温差范围时,近管壁与管中心的大,实验表
液体黏度相差亦大,加热和冷却时的区别更大,这时给热的关联式中,须加入一个包括壁温
下的黏度的校正项,按下式计算可得到较为满意的结果。
式中,α'为
Nu=0.027Re
0.8Pr-0.33
0.14
(5-64)
径,m;R
式中,除μ取壁温下液体的黏度,其他物理性质均按液体进、出口算术平均温度
rpIw
5.非圆
此时,
(5-69)
式中
第五章传
d2/d1=
Q=aA(t-1w)
A=ndl=π×0.012L
热171
而
Q-macp(t1-12)
(B)
A
(5-70)
按式(b)
代速率方程[式(a)]
msl=d2 up=×0.0122×0.32×852=0. 0308 kgs
(b)
20℃。
Q=0.0308×2.13×(95-65)=1.97 kJ•s或1970 W
本膨胀
解得
1970=(115.3-1/3)(π×0.0121)×60=261[2/3
3/2
关联
-()=20.7m
所需
于是
a=115.3×20.7-1/3=42.0W.m2.℃-1
/2=
本题由于润滑油的黏度大,流动为层流且给热系数小,需要相当长的换热管才能达到冷却目的(其实冷却的要求并不高)。对此,可选4管程、管长6m的换热器(相当于总管长为4×6=24m);换热面还留有一定余地。
【例5-16】某厂用冷却水冷却从反应器出来的有机液。按反应器目前的产量,要求从有机液中取走4×105kJ·h的热量。在仓库找到两个相同的单程换热器,其内径D=270mm,内装48根25mm×2.5mm、长为3m的钢管。壳程未加挡板,管间流体的给热系数可按当量直径计算。操作条件及物性见表5-10。
表5-10操作条件及物性数据
温度/℃
液体
质量流量定压比热容
入口
出口
密度
/kgh-1
热导率
kJ.kg1K
/kg·m-3
黏度/Pa·s
/W.m1K-1
有机液
63
T2
30000
2.261
950
0.172
1×10-3
28
t2
20000
4.187
1000
0.6210.742×10-3
试通过计算回答问题:(1)这两个换热器能否移走4×105kJ·h以上的热量?(2)应当并联还是串联(相对于有机液)使用?
解(1)先考虑串联使用。为便于清洗,且有机液的热导率较小而走管内。
①求有机液一侧的a1。管内径d1=0.02m,
总截面积
S1dn-0.02×48=0.0151 m2
30000
管内流速
=0.581 ms-
u-
3600×950×0.0151
diup
0.02×0.581×950≈11040
Re=1
1×10-3
Pr=Cp-2.26×103×1×10-3≈13.15
0.172
0.172
×1715×2.17=736W.m2.K-1
a=0. 023ARe0.8 Pr.3=0. 023
0.02
②求管外水侧的α2。管外径d2=0.025m,
管间截面
S2=(D2-d2n)=0.0337m2
170化工原理
量直径d
d=4×(管道截面积)
润湿周边
(5-69)
对于套管环隙中的给热,有专用的关联式。例如在Re=12000~220000,d2d
式中
1.65~17范围内,用水和空气等进行实验,所得关联式为
=0.02()
0.53Re0.8Pr1/3
而
(5-70
按式(b)
其他流体在环隙中做强制湍流时亦可应用此式。
代入速率方
【例5-15】润滑油在内径d=12 mm的换热管内,由95℃冷却到65℃;壁温 tw=20℃在本题涉及的温度下,油的物性可取:cp=2.13 kJ·kg1℃-1,λ=0.138 W·m℃-1;体膨,系数8=69×105℃1,在0℃时的密度po=899 kg•m3;黏度μ(cP)与温度T(K)的关联
解得
可用μ=4.75×10-6exp(5550/T)表示;管内流速u=0.32 m·s-l。求给热系数及所需
于是
本题由
换热管的长度。
冷却目的(
管长为4×6
80℃,此温度下的物性如下计算。
润滑油的比体积
1_1(1+△t)(m3·kg1),故
【例5-1
ppo
从有机液中
Po
899
=852 kgm-3
P-1+B△to
270mm,p
1+69×10~×(80-0)
热系数可按
黏度
5550
μ=4.75×10-6exp(273+80)=32.0 cP或 mPa.s
于是
Re=
dup_12×10-3×0.32×852102.2
μ
32×10-3
液体
由Re可知为层流,选用式(5-65):Nu=1.86(RePr)()0.14
有机液
水
式中
Pr-CPH-
2.13×103×32×103
0.138
=494
试通过
5550
=4.75×10-*exp(273+20)=800mPas
(2)应当并
而管长尚为未知,需利用给热速率方程去求取
解(
将已知值代入式(5-65)
①求
Nu=1.86×(102.2×800×0.012/)1/3(32/800)0.14
总
=1.86×(8.461-1/3)×0.637=10.031-1/3
-()Nu-
0.138
管
0.012×10.031-1/3=115.3-1/3
层流的a还要检验Gr值,以决定是否需对自然对流做校正
Gr=gd3p2B△t
μ2
9.81×0.0123×8522×69×10-5×60
现Gr远小于25000,不需校正。对于水平放置、直径不大的管,其内流体的自然对流受
(32×10-3)2
498
到较大的限制,对给热的影响一般不需考虑。
在给热速率方程(5-9a):q=α(t-tw)中,由于α及(t-tw)都是对整个换热面的平均值
②求
故热通量式(5-9a)可写成热流量的形式
管间
05,冷却时取为0.95。
第五章传热169
中待定的
由于求壁温会使计算复杂化,对工程问题可作以下简化:(/)
而提高准
【14】101-3kPs()下。空气在径m中流,度由180℃
220℃,平均流速为15m·s-1,试求空气与管内壁之间的给热系数。在液体加热时取为
本平均温
在(180+220)/2=200℃及101.3P下空气的物由六得。1一
0.0393 W•m-1K-1, μ=2. 60×10-5 Pa•s, p=0.746 kg•m3, Pr=0.680而
Re=
而定:对
dup0.025×15×0.746
μ
10℃),
Re>10000,应用式(5-63),得
2.60×10-5
=10760
(5-63)
Nu=0. 023Re0.8 Pr0.4=0.023×107600.8×0.6800.4
=0.023×1680×0.857=33.1
a=ANu0.0393×33.1
d
0.025
对空气,还可用较简单的式(5-63b),得
=52Wm2K1
mNoH=X(1-51x129v
(5-63a)
结果相近。
Nu=0.020Re0.8=0.020×1680=33.6
二1287×
=327.13
对层流
2.流体在圆形直管中作强制层流
邻近管
皮冷却
流体在圆形直管中做层流流动时,假定传热不影响速度分布,则热量传递完全依靠导热
中的
的方式进行。实际情况比较复杂,因为流体内部既有温差存在,必然附加有自然对流给热。
0.4。
只有在管径小和温差不大的情况下,即Gr<25000时,自然对流的影响才可以忽略;对于
这种情况,文献推荐求a的特征数关联式为
Nu=1.86()
1/3上0.14
63b)
Hw
(5-65)
应:
式(5-65)适用范围:Re<2300,6700>Pr>0.6,RePr(d/l)>10。当Gr>25000时,忽略
自然对流给热的影响,往往会造成很大的误差。此时式(5-65)右端应乘以一校正因子f1
f1=0.8(1+0.015Gr1/3)
(5-66)
式中,除是按壁温取值外,定性温度为流体进、出口的算术平均值。定型尺寸取为管内
径。在换热器设计中,应尽量避免在层流条件下进行传热,因为此时的给热系数很小。
3.圆形直管中的过渡流区
当Re=2000~10000时,还没有可靠的计算公式可用。作为粗略估计,可用Re>10
的(5-63)算出α值,然后乘以校正系数f2
f2=1-
6×10
(5-67)
Re1.8
4.弯曲管道内的给热系数
流体在弯管内流动时,会因离心力造成二次环流,使扰动加剧。其结果是使给热系数增
的
大,实验表明弯管中的a'约为直管中的(1+1.77d/R)倍,即
温
a'=(1+7d)a
(5-68)
式中,a'为弯管中的给热系数,W·m2K;a为直管中的给热系数,W·m2K1;d为管内
径,m;R为弯管轴的曲率半径,m。
此时,仍可采用上述式(5-63)~式(5-67)作近似计算,只是要将式中的管内径改为当
5.非圆形直管中的给热系数
172化工原理
20000
=0.165 ms-1
3600×1000×0.0337
故
u=
管外流速
4×0.0337
=0.0292m
de D+dn π(0. 27+0.025×48)
4S2
deup 0.0292×0.165×1000≈6490(过渡流区)
Re=
0.742×10-3
Pr=4.187×103×0. 742×10-3
=5.0
0.621
a2=0.023(A/de)Re0.8 Pr0.4
先求Re>104时
=0.023×(0.621/0.0292)×1120×1. 904≈1050 W.m2.K1校正到过渡流区
=a2(1-
R1.8=1050×(1-0. 0824)=963 Wm2K-1
6×105
查表5-5,取有机液侧污垢热阻R1=0.176×10~3m2·K·W-l,水侧污垢热阻R=0.58×10-3m2K·W-1,忽略钢管壁热阻,有
如图
I_I d2+
d2+Rd2+1
k a d1
0
0.025
10.025+0.176×10-3×
+0.58×10-3+
0.02
963
7360.02
=0.00170+0.00022+0.00058+0.00104=0.00354
解得
K=282W.m2K-1
解得
每台换热器的面积
A=πd2nl=11.3m2,串联时A=2×11.3=22.6m2
图
由于只知道热、冷流体的进口温度,采用-NTU法求出口温度较为方便。现mcp=
体并联
(30000/3600)×2.261=18.84 kJs1K1; ms2cp2=(20000/3600)×4.187=23.26 kJsKl,应
第
以热流体为准进行计算
KA
282×22.6
NTU=
=0.338
mslcpl18.84×103
CR=ms1Cpl=0.810
ms2Cp2
查逆流换热器的图5-21,因NTU太小而难准确。改按式(5-44)计算
1-exp[NTU(1-CR)]
1-exp(0.338×0.19)
CR-exp[NTU(1-CR)]0.81-exp(0.338×0.19)0.81-1.066
1-1.066=0.258
从E=T1-T2,得T1-T2=0.258×(63-28)=9.03℃
T1-t1
第
热流量
或
Q=ms1cp1(T1-T2)=18.84×9.03=170 kJs
温度提
Q=170×3600=6.12×105kJ.h1>4×105 kJh-l
故两个换热器串联时能符合要求。
150kg/ha0.581/20.21m+Re520
式(5-63)算出的a乘上校正系数f2
总热
f2=(1-
6×10
或
55201.8=0.89
174化工原理
流体在单根圆管外以垂直于该管的方向流过时,其前半周和后半周的情况并不相同,
由于各
(二)流体在管外强制对流
图5-27所示。正对流体流动方向的A点(φ=0处)称为驻
这里主流方向的流体速度为零,压力最大。随着增大,
边界层逐渐增厚,流体主流速度逐渐增大,压力逐渐下降
式中a1,
圆柱面后半周,则会发生边界层分离,形成旋涡。这种流动
1排、第2
对于
特点,必然使得在不同的φ处,具有不同的局部给热系数
流体垂直于单根圆管
局部给热系数的分布,关系到管壁圆周上的温度分布折流挡板
于在高温流体中操作的换热管(例如锅炉的高温过热器)
束,但在
图5-27
作管外流动的情况
于管束,
出圆周上的最高局部温度,有较大的实际意义。但在一般
的不断变
系数的计
管外装有
单根管外时复杂。管束的排列分直列和错列两种,如图5-28所示。
看图5-32
(103~10
十十十十十十十十十十十十十十00
或
0
电
(a)直列
在图
5-3
一
零
Alw
)0.14
女
0
轴
=
女女
00
成正三
X2
(b)错列
图5-28换热管的排列
流体在管束外横向流过时的给热系数可用下式计算
式中,
C1、C2和n的值见表5-11。
Nu=C1C2Re"Pr0.4
(5-71)
102
8
表5-11
直列流体垂直于管束时的C1、C2和n值
4
排数
2
错列
?
C2
1
C
0.6
0.171
C2
8
2
6
0.65
0.6
0.151
0.171
3
0.6
x1/d=1.2~3时
0.65
4
0.151
0.228
0.65
0.6
C1=1+0.1x1/d
2
0.151
0.290
0.6
x1/d>3时
0.290
C1=1.3
10
流体在错列的管束间通过时,受到阻拦,使湍动增强,故C2较大,即错列时的给热系数比直列时要大一些。从第3排以后,直列或错列的C2值亦即给热系数基本上不再改变。
式(5-71)适用于Re=5000~70000和x1/d=1.2~5,x2/d=1.2~5的范围。式中的物理常数取流体平均温度下的数值,定型尺寸取管外径,流速取各排最窄通道外的流速。
a1=0.023(A/d)Re0.8 Pr0.3 f2
第五章传热173
=0.023×(0.172/0.02)×985×2.17×0.89
=376Wm2K
2
T=63℃
12
图5-26
4=28℃
例5-16附图
如图5-26所示,冷流体仍为串联而流量不变,设物性常数等亦不变,则a2不变,有
11d2+Rd
Ka1d1kdi+rs
a2
10.025
3760.02+0.00022+0.00058+0.00104
=0.00516
解得
K=194W.m2.K-1
图5-26还示出,由于冷流体仍为串联,需求出它在两换热器之间的温度t2。又热流
体并联时的热容流量ms1Cp1比串联时更小,故在应用e-NTU法时仍应以热流体为准。第一换热器
NTU1=
194X11.3
(15000/3600)×2.261×10=0.233
CR=
msicp118. 84/2=0.405
ms2Cp223.26
1-exp[0.233×(1-0.405)]
1-1.149=0.200
0.405-exp[0.233×0.595]0.405-1.149
T1-T2=e(T1-t1)=0.200×35=7.0℃
Q1=ms1cp1(T1-T2)=(18.84/2)×7=65.9 kJ•s
t2=t1+msicp)(T-T2)=28+0.405×7=30.8℃
ms2cp2
第二换热器已设物性等不变,即与第一换热器的NTU及都相同,只是水的人口
温度提高为t2=30.8℃,有
TI-T2
ET1-12
T1-T2=e(T1-t2)=0.200×(63-30.8)=6.44
Q2-m1p1(T-)=(18.84)×6.44=60.7k1+s1
总热流量
Q=Q1+Q2=65.9+60.7=126.6 kJ•s
或
Q=126.6×3600=4.56×105kJh1(>4×105kJ.h1)可知热流体并联时也能满足需要。但串联比并联的效果要好,只是阻力损失也较大。
第五章传热175
司,如
由于各排的给热系数不同,可按下式求整个传热面积的平均α值
驻点,
a1A1+a2A2+a3A3+…
A1+A2+A3+…
层流
;到
排、第2排、第3排、……的传热面积。
动的
对于常用的列管式换热器,由于壳体是一个圆筒,故各排的管数不同,而且大多都装有
po
折流挡板(见图5-29),流体虽然大部分是横向流过管
。对
,但在绕过折流挡板时,则变更了流向,不是垂直
于管束,而是顺着管外的方向流动。由于流向和流速
折流挡板
,找
E
换热
的不断变化,Re>100时即达到湍流。这时管外给热
是流
系数的计算,要根据具体结构选用适宜的计算式。当
管外装有割去25%(直径)的圆缺形折流挡板时(参
流过
看图5-32),可以由图5-30求给热系数。当Re=2×
0
(103~106)之间时,亦可用下式计算
Nu=0.36Re0.55Pr
1/3()0.14
(5-72)
图5-29换热器壳程的流动情况
B-B-C一壳程流体通过圆缺形挡板缺口
a=0
0.55
0.36
()()1/3(瓷)0.14
的路径;A一少量流体通过管与挡板圆孔
或
间环隙的路径;E一少量流体通过壳内壁
与挡板间间隙的路径
(5-72a)
在图5-30和式(5-72)中,定性温度取流体温度的平均值,μ是指壁温下的流体黏度;(μ/)4可以简化,见管内湍流式(5-64)的说明。
轴向的当量直径d。要根据管的排列情况决定。如图5-31所示,管成正方形排列时
4(t2-nd/4)
de=
4t2
(5-73)
πd。
πd。
成正三角形排列时
de—(2-d)
(5-73a)
式中,t为相邻两管中心距;d。为管外径。
1)
102
86
4
二2
(a)正方形
0864
O
dnN
o
O
2
o〇〇〇〇〇〇
102468102246
8103246810
(b)正三角形
Re
图5-32换热器的
为
图5-31换热管
折流挡板
图5-30管壳式换热器壳
比
程给热系数计算用图
的排列
(5-74)
的
管外的流速可以根据流体流过的最大截面积S。计算
So=h(D-ncdo)
式中,h为两块折流挡板之间的距离;D为换热器壳径;n。为管束中心线上的管数(管数最多176化工原理
常用折流挡板的形式如图5-32所示,称为圆缺形(或弓形)折流挡板。割去部分的
【例
度约占直径的25%。显然,在管间安装折流挡板,可以加大流速,并使流动方向不断变
周围空气
从而可使给热系数增大;但同时也增加了流体流动的阻力。
流量。
如果列管换热器的管间没有折流挡板,管外的流体将平行于管束而流动,此时的可做
解
管内强制对流时的公式作近似计算,但需将管内径改为管间当量直径。
K1;其他
(三)提高给热系数的途径
随着Re的增加,流体流型从层流转变为湍流时,给热系数α显著增大,所以应力10-5Pas
热、冷流体皆在换热器中达到湍流流动。
而Gr
湍流时,常应用式(5-63)或式(5-63b)求圆形直管内的a,若将式中所有物性参数合为常数A、则得a=Au.8/d0.2。可见,a与流速的0.8次方成正比,而与管径的0.2次方
根据表5
流体横向流过管束作湍流流动时,在管外加折流挡板的情况下,应用式(5-72)求a理,将物性常数合并成B,则得α=Bu0-55/d45。可见,管外加有折流挡板时,给热系数与流速的0.55次方成正比,而与当量直径的0.45次方成反比。因此设置折流挡板,提高流
这是一
和缩小管子的当量直径,对加大管外给热系数均有较显著的作用。
给热热
总之,不论管内或管外,提高流速都能增大给热系数,但随着流速的增加,阻力损失
五、
要大致按流速的平方迅速增加,因此设计换热器时,应当根据具体情况选择优化的流速
当纯
除加大流速外,在管内装置添加物如麻花铁,选用波纹管等,均能增加流体的湍流程度,从而增大给热系数,但阻力损失或能量消耗也随之增加。
凝液能润
四、流体作自然对流时的给热系数
若冷凝壁
大空间(指边界层不受干扰)中流体作自然对流时,给热的特征数普遍关联式为式(
冷凝液不
60):Nu=f(Gr,Pr);在一定范围内可用以下的幂函数表示
重又露出
Nu=C(GrPr)"
盖着一层
或
(5-75)
a=C(2RBAt3×C)
凝时的
(5-75a)
通常会
不同几何状况下所得的实验数据都表明:Nu对GrPr在双对数坐标上标绘,都是一条
下面仅
稍向上弯的曲线。可分段近似用直线式关联,见表5-12。式中,定性温度取壁温t和流体
如
进出口平均温度tm
(-)
的平均值,称为膜温,定型尺寸见表5-12。
蒸气的
蒸气所
表5-12式(5-75)中的C、n值和定型尺寸
方式通
加热表面形状位置
GrPr
n
10~104
C
定型尺寸
垂直平板及圆柱
104~109
1/6
1.23
式中,
109~1013
1/4
1/3
0.59
高度H
厚度。
水平圆柱体
10~103
0.1
104~109
1/6
同
1/4
1.02
109~1012
将
水平板热面朝上或水平
1/3
0.53
外径d。
板冷面朝下
2×104~8×106
0.13
8×106~1011
1/4
1/3
0.54
式中,
水平板热面朝下或水平
0.15
正方形取边长
板冷面朝上
105~1011
长方形取两边平均值
平均给
1/5
圆盘取0.9d
0.58
狭长条取短边
显
式(5-7
最多)。
分的宽
【例5-17】有一垂直蒸气管,外径100mm,长3.5m,管外壁温度为110℃。若
第五章传热177
变更,
围空气温度为30℃,试计算单位时间内由于自然对流而散失于周围空气中的热流量。
可用
解定性温度(110+30)/2=70℃。在此温度下,空气的3=1/(273+70)=2.92×1032:其他物理性质由附录六查得p=1.029 kgm3,A=2.966×10-Wm3+℃p=2.06×10-5 Pas, Pr=0. 694。
求使
Gr=gH3p23t_9.81×3.53×1.0292×2.92×10-3×(110-30)
148
(2.06×10-5)2
合并
GrPr=2.45×1011×0.694=1.70×10u
=2.45×101
方成
根据表5-12,查C=0.1,n=1/3,得
Nu=0.1(GrPr)1/3=0.1×(1.70×1011)1/3=554
。同
a=Nu=554×
2.966×10-2
数与
3.5-=4.70W.m2.℃-1
流速
这是一个很小的给热系数值(较表5-8范围的低限还稍小)
热热流量Q=αA△t=4.7×(π×0.1×3.5)×(110-30)=413W
夫也
五、蒸气冷凝时的给热系数
当纯的饱和蒸气与低于饱和温度的壁面相接触时,蒸气将放出潜热并冷凝成液体。若冷
程
凝液能润湿壁面,并形成一层完整的液膜向下流动,称为膜状冷凝;
壁面上存在一层油类物质,或蒸气中油类或脂类物质,
热流方向
冷凝液不能润湿壁面,结成滴状小液珠,逐渐长大,最终从壁面落下,
5
重又露出冷凝面,则称为滴状冷凝。由于膜状冷凝时,壁面上始终覆
盖着一层液膜,形成壁面和冷凝蒸气之间的主要传热阻力,故滴状冷
一一一一一一一一一一一一一一一
纯饱和蒸气
5)
凝时的给热系数,比膜状冷凝时要大几倍到十几倍。两种方式的冷凝
ts
通常会同时存在,但在工业生产中,大多数情况下以膜状冷凝为主,
=8
a)
下面仅讨论膜状冷凝情况。
条
如图5-33所示,冷凝液在重力作用下沿壁面向下流动,同时由于图5-33膜状冷凝
蒸气的冷凝,新的冷凝液不断加入,故使液膜厚度从上至下不断增加。
蒸气所放出的潜热,必须通过冷凝液膜传到壁面,若液膜沿壁面作层流流动,热量以导热的
方式通过液膜,则根据傅里叶定律
(a)
式中,M为冷凝给热温差,即跨过冷凝液膜两侧的温差;为距壁顶端距离为处的液膜
厚度。
同时,此项热量也可用给热方程式表示:dQ=a(dA)At。
将上两式比较,得
ax=/8x
式中,a2为距壁顶端距离x处的局部给热系数。当x增大,因62随之增厚,故a2减小。
(5-76)
平均给热系数
a-ada-
显然,a2的大小取决于冷凝液膜的厚度和热导率,只要求出,与x的关系,即可由
式(5-76)得出平均的给热系数。
180化工原理
Q-msr _Mr
对于垂直管、板,在层流(Re<1800)时,△t=
直接整理成Re的函数。
aa abh aH代人式(5-79b)得
1/4
a=1.13
=1.13()
a3=1. 87Re-1/3
1/3
(5-81)
整理后得
a*=1.87Re-1/3
(5-81a)
1/3
或
12
式中,a*为冷凝特征数,无量纲,a*=a2
当液膜中的液体为湍流流动(Re>1800)时
a*=0.0077Re0.4
(5-82)
可将层流和湍流的公式绘制在同一张图中,如图5-38所示。
湍流
以上公主
0
层流
1.0
不凝性气体
0.8
0.6
达液膜表面
0.4
0.2
推荐值
在冷凝过程
理论值
【例5-
0.1
102234681032345681023456810
Re
管径100
图5-38冷凝液膜中Re对a的影响
时的给热
解
同理,对于水平管,将式(5-80)整理后得到特征数关联式
959 kgm
a2=a()=1.51(M)-1/3
(5-83)
100℃,r
M'=ms/l
(1)
式中,1为管长,m;M'为单位水平管长的冷凝液质量流量,kg·sm-
数,然后
工业中的许多冷凝器都由水平管束组成,蒸气在水平管束外冷凝时有以下特点:就上面第一排管而言,它的冷凝情况与水平放置的单根圆管的冷凝情况相同;对于下面其他各排管,其冷凝液的流动情况还要受到在它上面各排管所流下的冷凝液的影响。
对于在垂直方向上由n根管子组成的管束,在各管上跨过液层的温差△=t一t。相同的条件下,努塞尔假定上排管流下的冷凝液是平稳地流到下排管而使液膜增厚;如图5-39(a)所
校验Re
示,则只需将定型尺寸由do改成ndo而得出管束的平均给热系数
式中
a=0.725
1/4
(5-80a)
因而
und。△t
但是,按式(5-80a)计算所得的平均a较实验结果偏低,尤其是在垂直方向上管数n较所示,于是下一排管上的冷凝液膜并不像上述的那样厚,同时附加的扰动还会加快传热,
故假定为
究表明,这些影响与冷凝液负荷M、冷凝液的物性(主要是黏度和密度等)以及管间距等
(2)
因素有关。总之,这是一个很复杂的问题,目前还没有总结出普遍适用的规律。在缺乏数据
管水平放
时,可在式(5-80)中用n2/3do代替do。
若为过热蒸气的冷凝,在壁面温度低于饱和温度的情况下,仍可应用以上公式求a,式中的△t仍为饱和温度与壁温的温差,只是冷凝潜热一项应改为过热蒸气冷凝成饱和液体时
故单根
放出的热量(比饱和蒸气稍大)
度、热导率和
中,蒸气的冷凝潜热按饱和温度t取值;其余物性均按液膜平均温度m=(+t,)/2取值。
对于与水平面成夹角中的斜壁,如图5-35所示,同理可得类似式(5-79)的方程为
第五章传热179
4所示,微元
a=0.943×
摩擦力可以忽
r2gsinp 1/
图5-36所示为蒸气在单根水平管外冷凝时液膜的流动情况,通常管径比较小,可认为液膜内的流体为
pH
流流动,与直立壁面不同的是液膜沿管外壁流动时,重力作用的方向和液流动的方向不一致,而且
(5-79a)
sing沿圆周连续变化。
图5-35蒸气在斜壁上冷凝
图5-36水平管外的膜状冷凝
塞尔曾用积分法求得水平管外蒸气冷凝时的给热系数:
a=0.725×
()
(5-80)
式中,定型尺寸为管外径d。
壁面呈垂
(二)实验结果
对于水平单管,实验数据和上述理论公式所求得的结果符合得很好,即a=0.725×rp2g31/4
。至于垂直管和垂直板,即使冷凝液沿壁面为层流流动,由于推导过程中所作udoAt
的假定不能完全保证,例如液膜流速较大时液膜表面将出现波纹,故大多数实验值比由理论
+d2),
公式所求得的结果大20%左右。修正后的计算公式为
()
1/
a=1.13
(5-79b)
,并假
式(5-79b)是在层流条件下得出的。若壁面较长,热通量较大时,在离壁顶端一定距离
液层的
,由于冷凝液积累的结果,流动将转变为流,如图5-37所
示。与强制对流一样,可用Re作为确定层流和湍流的准则。若层流
冷凝液流过的截面用S表示,润湿周边用b表示,质量流量用m
表示,并将单位长度润湿周边上冷凝液的质量流量称为冷凝负
(5-77)
荷,用M表示(M=m。/b),则
湍流
Re=dep_(4 S/6)(ms/s)
μ
图5-37蒸气在垂
5-78)
4 ms1b_4M
直壁面上冷凝
当Re<1800时膜内流体做层流流动;Re>1800时则为湍流流动。
μ
-79)
由于Re对确定流体在冷凝液膜中的流动状态有重要作用,故蒸气冷凝时的给热系数常
μ
178化工原理
其中,蒸气
选学内容
对于与
图5-34所示为冷凝液膜沿垂直壁面向下作层流流动的情况。设冷凝过程中,冷凝液的密度、热导率(一)蒸气冷凝时给热系数的理论推导
黏度可作为常数处理。在冷凝液膜内取一微元,分析其在某瞬间的受力和运动情况。如图5-34所示,微边长在x、y轴方向分别取dx、(62一y),在z轴方向取l为单位长度。又假定蒸气对液膜的摩擦力可以息
图5-3
略,在稳定情况下,微元所受向下的重力和壁面的阻力达到平衡,即
层流流动。
dx(6x-y)×l×pg=μ(dx×l)
gsing沿圆
或
du,=2(&2-y)dy
积分得
u2=(&2y-y2)+C
式中,u2为





















离壁面y、距顶端x处下流液体的速度。
orH
dx
x
duy
μdx
dy
pg(δ,-y)dx
努塞
dx
y
x图5-34蒸气在垂直壁面上的冷凝
式中,定
由于与壁面接触处,液体流速为零,即当y=0处,u=0,故常数项C=0。距顶端x、在与壁面直的截面上液体的平均速度u为
。)
(二
在距顶端x处下流的质量流量为
对
rp2ga
m3=po2×l×u
pd。
由于蒸气在垂直壁面上冷凝的结果,从距顶端x到(x+dx)处,液膜厚度由δ,增加到(8+d)
3
液体质量流量的增量为
的假定
公式所
=do
da
da=p2go do,
蒸气冷凝时放出的热量,必等于以导热方式通过冷凝液膜的热量。若蒸气的冷凝潜热用r表示,并
0
定液膜和壁面接触处的温度等于壁温t,而液膜和蒸气接触处的温度等于蒸气饱和温度t,则跨过液层的
式
温差△t=t。-t。如假定此温差为一定值,则
处,由
r ams dr=rp2go.do,
示。与
将上式在x=0至x=x间积分可求得距顶端x处的冷凝液膜厚度为
=dx×lX
冷凝液
表示,
因此,距顶端x处的局部给热系数为
=()
(5-77)
荷,月
()"
若垂直壁面的总高度为H,则平均给热系数为
--()"I-()" -.()"
(5-78)
当Re
(5-79)
(5-79b)得到
第五章传热181
(5-81)
(5-81a)
(5-82)
(a)液膜平稳下流
(b)液膜下流时产生撞击和飞溅
图5-39管束中液膜下流情况
以上公式是按纯净的饱和蒸气在清洁的表面上冷凝时建立的。若蒸气中含有空气或其他达液膜表面才能冷凝,这就相当于增加了一项大的热阻,使冷凝给热系数急剧下降,因此,在冷凝过程中及时排除不凝性气体甚为重要。
【例5-18】101.3 kPa(绝)下的水蒸气在单根管外冷凝(管内通空气作为冷却剂)。管径100mm,管长1.5m,管壁温度为98℃。试计算(1)若管垂直放置,水蒸气冷凝时的给热系数;(2)若管水平放置,重新计算冷凝给热系数。
解冷凝液膜平均温度(100+98)/2=99℃下,水的物性常数查附录五,内插得p=959 kg•m3; μ=0. 286 mPas; λ=0.683 WmKl; 101.3 kPa(绝)下的水蒸气, t=
(5-83)
100C,r=2257 KJ.KG - Башкы бет。
(1)管垂直放置时先假定液膜中的液体为层流流动,由式(5-79b)求平均给热系数,然后再校验Re是否在层流范围内。按垂直面的式(5-79b)得
点:就上面
1/4
2258×103×9593×9.81X0.68331
=1.13×
其他各排
a=1.13o g
uH△t
0.286×10-3×1.5×(100-98)
=1.13×(7.56×1015)1/4=10540W.m2.K
相同的条
-39(a)所
校验Re数
Re-()()/-
式中
Q=aA△t=10540π×0.1×1.5×(100-98)≈9930 W
4×9930
(5-80a)
因而
Re=X0.1×2258×103×0.256×10
管数n较
=219(<1800)
5-39(b)
传热。研
(2)平放(5-80)和式(5-79b),长为1.5m、外为0.1m故假定为层流是正确的。
管间距等
管水平放置和垂直放置时的给热系数a与a的比值为
()
=1.263
缺乏数据
a'0.725(H)0.642×
a1.13
求α,式
和液体时
故单根管水平放置时的给热系数为
a'=1.263×10540=13310W.m2K1
182化工原理
【例5-19】一套管换热器水平放置,其内管是22mm×1mm的铜管,管间通人110℃饱和水蒸气,使内管中的冷水水温从25℃升至45℃,现已知水侧的给热系数为
以下对
4800 W·m2K1,垢层及间壁总热阻为0.0007 m2·K·W1,试计算冷凝给热系数a1和传解本题在应用水平管的式(5-80)时,因壁温t未知,故冷凝给热温差△t1=t-热系数K。
变化不大,可按比t稍低(如设t=t。3=110—3=107℃)取值,以后再核对。
与原设t行
按t=107℃查附录五(内插),可得
p=953 kg•m3, λ=0.684 W•m-2C-1, μ=0.266 mPas
于是
且110℃下,r=2230kJ·kgl,代人式(5-80)得
1/4
2230×103×9532×9.81×0.68431/
a1=0.725
=0.725×
ud。At
0.266×103×0.022△1
=0.725×(1.087×1018)1/4△1
再按新
(a)
含a1及At1的另一关系是基于管外壁面积的冷凝给热速率方程
阻是污垢
q1=a1△t1
(b)
置,以上式
对式中的q1可列出基于管外壁的传热速率方程
Wm2℃
q1=K1△tm
本题在
(e)
关于△tm,因换热管两端总温差之比
题是物性的
ts-t1110-2585
ts-t2110-4565(<2)
六、液
在锅炉
可取
85+65
Atm=2=75℃
为两种情况
再考察K1
是由于自然
称为管内沸
(d)
复杂的气-液
式中a1虽未知,但水蒸气的冷凝给热系数通常甚大(10000以上),其热阻占总热阻的
本章主
比例较小,故误差对K1的影响不大。现暂根据上一例题设a1=13000W·m2℃-1,得
(一)
1_1
K113000+0.0007+48
沸腾给
22
4800×20=(0.77+7+2.29)×10-
态,即液体
=10.06×10-4m2.C.W-1
的平均温度
K1=994W.m2.C-1
长大需要能
以上对总热阻1/K;的计算中,可知1/a占1/K;的比例不到1/10,将△m及K代
式(c),得
速率。例如
的一薄层液
tw,如图 5
将所得q1值代入式(b),得q1=994×75≈74600W
下面仍
a1△t1=74600W
平的点上形
为从式(a)中消去△t1,将式(e)两边开4次方再去除式(a),得
(e)
继续汽化而
空间被周围
故
4=0.725×1400)=1417
形成,有
α1=14174/3=15910Wm2℃-1
随时填补,
(④)
化时的大很
液体沸
通入
以下对得出的a1作核算。先考察膜温t(·由式(e)
第五章传热183
数为
和传
△t1=1s-tw=
q174600
a115910
=4.69℃
-tw
tw≈ts-△t1=105.3"℃,t4=
110+105.3
度的
与原设t很接近,无需对物性做调整。重新按式(d)计算K
2
=107.7℃
K-10
+0.0007+0.000229=1008Wm2C-1
于是
q1=1008×75=75600W
8/4=0.725×(1.087×1018/75600)1/4=1412
a1
a1=14124/3=15840W•m2℃
再按新得出的a1去算K1,结果与式()并无差别。其实,本题由于传热的主要热
(g)
(a)
是污垢热阻,其估计的误差较大,且随时间延长而增大;冷凝热阻本身只占次要位
(b)
置,以上式(f)~式(g)的复算并无必要;答案取为α1=15840 W·m2℃-1,K1=1008W.m2℃-1。
本题在需要试差时先做分析,找出计算最稳定的途径(初值对结果的影响最小;本
(c)
是物性的变化很小,α1对K1的影响很小),这一思路在含试差问题的求解中很重要。六、液体沸腾时的给热系数
在锅炉、蒸发器等设备中,都是将液体加热使之沸腾并产生蒸气。工业上液体沸腾可分为两种情况:一种是将加热面浸于液层中,液体在加热面外的大容积内沸腾,液体的运动只是由于自然对流和气泡扰动所引起;另一种是液体在管内流动的同时在管内壁发生的沸腾,称为管内沸腾。这时在加热面上产生的气泡不能自由浮升,而是被迫与液体一起流动,出现复杂的气-液两相流动状态,其传热机理较大容积沸腾更为复杂。
d)
本章主要讨论大容积沸腾的情况。
的
(一)沸腾现象
沸腾给热过程最主要的特征是液体内部有气泡生成。一般认为气、液两相处于平衡状态,即液体的沸点等于该液体所处压力下相对应的饱和温度t。但实验测定表明,沸腾液体的平均温度t1略高于饱和温度t,即液体处于稍过热的状态;过热的原因是气泡的生成和
长大需要能量克服表面张力;温差(t一)称为过热度,其大小取决于液体的物性及汽化率。例如在常压下,沸腾水的平均温度往往比饱和温度高0.4~0.8℃。而在紧靠加热面
人
的一层液体中,温度急剧升高,直到液体和加热面直接接触处,其温度等于加热面的温度
s,如图5-40所示。这里的过热度最大,△t=tw-t,也就是给热温差。
下面仍以水的沸腾作为讨论对象。实际观察表明,气泡只是在加热面上某些凹凸不
平的点上形成。这些形成气泡的点称为汽化核心。当形成气化核心以后,周围的液体
续汽化而其体积不断增大。当气泡长大到某一直径后,就会脱离壁面上升,让出的
e)
空间被周围温度较低的液体所置换。所以,从一批气泡脱离加热面到另一批新气泡的形成,有一段重新过热的间隔时间。气泡的不断形成、长大和脱离加热面、周围液体
时填补,引起贴壁液体层的剧烈搅动,从而使液体沸腾时的给热系数可以比无相变
f)
液体沸腾给热的规律,可以通过图5-41来加以说明。
化时的大很多。
184化工原理
1.大容积饱
由于气泡产
109
响甚为复杂,因
108
_自然对流核状沸腾膜状沸腾
理出核状沸腾的
107
(1)
106
105
式中,Cwe为取
2明104
为饱和液体的定
103
102
水面
tw-ts; r, p
水
101
100.4℃100℃蒸汽
蒸气的密度,
1.0
10
0.1
100
100
6
78
At/K
1000
对于其他液体
I2345
0离加热面距离/cm
式(5-84)
图5-41水沸腾时温差和
图5-40
从下面加热时,沸腾水温
给热系数的关系
2.0之间变动。
度的变化(常压,t=109.1℃)
常压下当壁温t与水的饱和温度t。之间的温差较小时,只在加热面少量汽化核心上形
表面-液体
成气泡,而且气泡的长大速率很慢,边界层受到的搅动不大,因此,给热以自然对流为主,
水铜
给热系数随温差增大的规律与自然对流时差别不大。
随着给热温差△t=tw-t。的加大,汽化核心数增
水铂
水-黄铜
2
2
加,气泡长大速率也较快,对液体产生强烈的搅动作
正丁醇-铜
106
106
用,使给热系数随温差增加而急剧增大(与△t的2~3
异丙醇-铜
5
5
次方成正比),这时的沸腾称为核状沸腾。
9
2
2
随着△t继续增加,汽化核心数和气泡长大速率
正戊烷-铬
I105
10
进一步增加,直到大量气泡在加热表面上汇合,形
苯-铬
5
5
E
成一层蒸气膜,热量必须通过此蒸气膜才能传递到
2
2-.E.8液体主流中去。由于蒸气的热导率比液体的小得多
(2)
10
104
从而使给热系数迅速下降,这时的沸腾称为膜状
5
即
沸腾。
2
103
当△t再加大时,由于加热面具有甚高的温度,辐
10
式中,d为
2
5102050100
射的影响增大,使给热系数重又有所增大。
温差△/℃→
由核状沸腾转变为膜状沸腾时的温差称为临界
图5-42水在100℃下沸腾时,温度差。这时的热通量称为临界热通量。
之间的接触
差对给热系数和给热通量的影响
由此可知,工业上,一般应控制在核状沸腾
作。如果超过临界热通量,给热系数α将迅速下降,因()
为
管烧毁的严重事故。对于常压下的水,在大容积内沸腾时的给热系数、热通量和温差之间的反映汽化速
关系,如图5-42所示。由图可知,临界温差为22℃,这时的给热系数为51kW·m2K,临界热通量为1100kW·m20
(二)沸腾给热计算及其影响因素
腾的影响;
定压比热容
结果有些差别。
0
KH
时的实验数据
1大容积饱和核状沸腾
第五章传热185
由于气泡产生和运动的规律,以及加热表面状况对不同液体在核状沸腾下传热速率的影
响甚为复杂,因而至今还难以从理论上求解。一般采用量纲分析法,通过大量的实验数据整
出核状沸腾的特征数关联式。下面推荐两个工业计算上常用的计算式
(1)
cp△t
rPrs
=Cweq
0.33
(.)
中,C为取决于加热表面-液体组合情况的经验常数,其数值参阅表5-13c、Pr分别
(5-84)
气的密度,kg•m3;为液体-蒸气界面的表面张力,N·ml;s为系数,对于水s=1.0,
对于其他液体s=1.7。
式(5-84)适用于单组分饱和液体在清洁壁面上的核状沸腾。对于沾污的表面,在0.8~
20之间变动。
形
表面液体组合情况
表5-13不同表面-液体组合情况的C值
Cwe
表面-液体组合情况
。
Cwe
水铜
0.013
乙醇铬
0.027
水铂
0.013
水-金刚砂磨光的铜
增
0.0128
水黄铜
0.0060
正戊烷-金刚砂磨光的铜
0.0154
作
正丁醇-铜
0.00305
四氯化碳-金刚砂磨光的铜
0.0070
3
异丙醇-铜
0.00225
水-磨光的不锈钢
0.0080
0.015
水-化学腐蚀的不锈钢
0.0133
率
正戊烷-铬
苯铬
0.010
水-机械磨光的不锈钢
0.0132
到
(2)
Nu=3.25×10-4Pe0.6 Ga0.125K0.7
0.125
1
)0
(d)
(5-85)
犬
即
adb=3.25×10-4
,其中,0为壁面和自由液面
式中,d为气泡脱离加热面时的直径,db=0.020√(p1-p)g
,m;Pe
之间的接触角,(),在一般钢制设备中蒸发水溶液时0≈50°,即d≈
(a-0)8
,称为导温系数,Pe
9
相当于气速,而这里a=A
CpO
为克来(Peclet)数,rpy
反映汽化速率对沸腾的影响;(d)
为伽利略数,表示重力作用下流体流动情况对沸
的影响;Kp(一
pdb为反映压力p影响的特征数;λ、cp、μ、1分别为液体的热导率、
定压比热容、黏度和密度;p为饱和蒸气的密度。
0KaraH等C6opHa pa6or KIHMC (1957)推荐式(5-85)用于计算管内沸腾的a。但它用在综合大容积沸腾时的实验数据时也能符合(大连工学院学刊,第8期,1958)。
186化工原理101.3 kPa(绝)下的水在机械磨光的不锈钢容器内沸腾,钢表面保持
(3)
【例5-20】
113.9℃。试求给热系数a。
度p下降,
解沸腾时的给热温差=113.9-100=13.9℃,由图5-41或图5-42可知沸腾在核状沸
(4)
而加大,
腾区。
(1)根据式(5-84)求取g和a。
般比水的
对于水-不锈钢组合由表5-13得C=0.0132,水与水蒸气的物性为:c
(5)
4.22 kJkg3K1; p=958.4 kg•m3; r=2257 kJ•kg1; =0. 597 kg•m3; a=58.84x
管也有区
10-3N.m1; Pr=1.75;μ=28.24×105Pas; s=1
的管外产
将这些数据代入式(5-84),得
差、压力
q
58.84×10-3
0.33
4220×13.9=0.013228.24×10-5×2257×103×9.81×(958.4-0.597)
2257×103×1.75
、
一、
解得q=362200W·m2
前第
故
--26000Wm2K
出辐射能
(2)根据式(5-85)计算a
体吸收而
那一部分
-3.25×10())()
都会不停
两过程的
对于水
d=(m-a)
a=0.0025m,a=1.69×10-7m2·s-1,
时,辐射
热射
A=0.682W.m1K1,v=0.295×10-6m2.s-1
一介质中
a×0.0025=3.25×10
a△t×0.0025
0.6
不能透过
0.682
2258×103×0.597×1.69×10
如图
9.81×0.00253×958.420.1251.013X105X0.00250.7
(0.295×10-6)2
一部分能
58.84×10-3
=3.25×10-4a0.6×0.15240.6×(1.76×106)0.125×43100.7
透过物体
a0.4=60.56
两个公式的计算结果基本相符。
a=28500W.m2.K-1
即
或
2.影响大容积核状沸腾给热的因素
(1)表面粗糙度和表面物理性质然式(5-85)用C考液体壁面组合
式中,A
能
黑体,但
能
再继续增加粗糙度并不能进一步强化沸腾给热。对工业设备来讲,由于氧化、结垢等原因、
的,但
能
在当设备使用一段时间后,对a不再有明显影响。在计算公式中没有考虑加热表面材料的物
的气体
理性质对沸腾给热的影响,主要体现在液体和壁面的润湿能力上,式(5-84)中的C和
不对称
式(5-85)中的d内所含的0在一定程度上反映了这种影响。
吸
(2)沸腾给热温差前已述及,温差△t(=tw-t)是影响沸腾给热的重要因素,在常
的波长
用的核状沸腾范围内,其a与△t的2~3次方成正比(见图5-41或图5-42)。
黑
保持
(3)操作压力当沸腾的压力p增大,饱和温度也随之升高,使液体的表面张力。和黏度μ下降,有利于气泡的形成和脱离,在同样△t下的α将增大。第五章传热187
状沸
(4)液体性质液体的物性对沸腾给热有重要影响。a通常随热导率λ和密度p的增大面加大,随a和μ的增大而减小。盐类水溶液和有机物的a在同样的△r(或q)及p下,一比水的a要小。
4×
也有区别。对于常见的水平管束,由于最下一排管外产生的气泡,在上浮过程中对其上面
的管外产生附加扰动,故管束的平均给热系数比单管大,其程度与管排的间距及沸腾的温
、压力等条件有关。
33
第五节辐射传热
一、基本概念
前第一节中提到,物体通过电磁波来传递能量的过程,称为辐射。物体可由不同原因发
出辐射能,其中由于热而发出辐射能的过程称为热辐射。电磁波的波长范围极广,但能被物
吸收而转变为热能的辐射线主要为可见光和红外线两波段,即波长在0.4~40μm之间的
一部分,统称为热射线。自然界中所有物体(其热力学温度高于零度)除下述透热体外。
不停地发能时,不断吸来外界物发来的能和吸收
程的综合结果,造成物之间的能量传递,称为辐传热。当物体与周的温度相同
时,辐射传热量虽为零,但辐射与吸收过程仍在不断进行。
热射线和可见光一样,具有反射、折射和吸收的特性,服从光的反射和折射定律,在均
一介质中作直线传播,在真空和一些气体中可以完全透过。但热射线
Q
不能透过工业上常见的绝大多数固体或液体。
如图5-43所示,投射在某一物体表面上的总辐射能为Q,其中有
一部分能量QA被吸收,一部分能量QR被反射,另一部分能量QD则
透过物体。根据能量守恒定律,得
QA+QR+QD=Q
图5-43辐射能的吸
即
QA+=1
收、反射和透过
或
A'+R+D=1
中,A'(=QA/Q)为吸收率;R(=QR/Q)为反射率;D(=QD/Q)为透过率。
清况,
能全部吸收辐射能的,即A'=1的物体称为绝对黑体或简称黑体。自然界中并不存在绝对
糙表
黑,但有些物体相当接近于黑体。如没有光泽的黑漆表面,其吸收率A'=0.96~0.98
穴反
能部反射辐射能的,即R=1的物体称为绝对白体或镜体。实际上镜体也是不存在
限后,
的,但有些物体相当接近于镜体,如表面磨光的铜,其反射率R可达0.97。
原因,
能透过全部辐射能的,即D=1的物体称为透热体。例如,由单原子或对称双原子构成
糙度
的气体(如He、O2、N2和H2等),在工业常见温度范围内可视为透热体。多原子气体和
的物
环对称的双原子气体则能够有选择地吸收和发射某些波段内的辐射能。
we和
吸收率A'、反射率R和透过率D的大小取决于物体的种类、温度、表面状况和辐射线
的波长等,一般来说,表面粗糙的物体吸收率较大。
在常
黑体在一定温度下,单位表面积,单位时间内所发射的全部辐射能(波长从=0到A=
二、物体的发射能力与斯蒂芬-波尔茨曼定律
∞),称为黑体在该温度下的发射能力,以Eo表示,单位为W·m2。
188化工原理
E必小于黑
在一定温度下,设在波长λ至(+△)范围内黑体的发射能力为△E。,则
为了处
△Eo_dEo
o A da
lim
(5-86)
多工程材料
黑体的单色发射能力,以E表示,它是指黑体在一定温度下,单位表面积、单位时间
射,使问题
度,其值小
内发射的某一特定波长的能量。Exo随温度和波长而变化的规律,已经由普朗克根据量子理
论得出下列关系式,称为普朗克定律
材
CiA-5
EAO-CC2/AT-1
(5-87)
红砖
耐火砖
式中,E为单色发射能力,Wmm1;为波长,m;T为黑体的热力学温度,K;C1为
钢板(氧化的
常数,其值为3.743×10-16W•m2;C2为常数,其值为1.4387×10=2m•K。
钢板(磨光的
铸铁(氧化的
图5-44示出式(5-87)的具体关系。由图可知,每一等温曲线在λ从零增大时,E也
从零迅速增加,达到一最高值后,又随λ的继续增大而减小。如图5-44(a)所示,在常见
灰体的
的工业高温下,辐射能主要集中在λ=0.8~10μm范围内;图5-44(b)示出温度高于400
K后,可见光(A≈0.4~0.7μm)所占的比重才较大。普朗克的理论值与实验值能很好地
式中,εCo
符合。
3.489
11.63
三、
9.304
1400K
6000K
克希
E2.326200K
6.978
3
EEo
设有
2
黑体,T
壁面发射
1.163
4.652
5000K
灰体,T
2
平壁。以
1000K
2.326
如图5-46
800K
4000K
3000K
实际物体
量E1投
02468
0.40.8
1.2
投射于壁
/um
a/um
白体,T
(1-A1)
(a)较低温度
(b)较高温度
面温度相
图5-44普朗克定律的图示
图5-45黑体、某实际物体和
收的能量
灰体的单色辐射分布
黑体的发射能力E。可由式(5-87)示出的E关于λ从0~∞的全部范围内积分而得
因具有B
积分结果为
E-E-
E=0T=C()
(5-88)
式(
式中,a为黑体的发射常数或斯帝芬-波尔茨曼常数,其值为5.669×10-8W·m2K+;C为
收率的比
体的温度
表明绝对黑体的发射能力与热力学温度的4次方成正比。
在同一
关于在下,实体与体特的异,在于的单色
不相同
收的分
四
可以计算m的值,单位为μm。
工
灰体。
必小于黑体的Exo,而且比值E;/E随波长)而变动,如图5-45所示,
为了处理工程问题的方便,提出了灰体的概念:其E/Em为一常数e。并示于图5-45中。许
第五章传热189
(5-86)
单位时间
据量子理
《工程材料都可近似作为灰体,这样就不必考虑辐射能随波长的分布,而从黑体的规律去计算时,使问题大为简化。不随波长而变的比值e通称为黑度,它取决于物体的种类。表面状况和温度,其值小于1。某些材料的e值见表5-14。
温度/℃
表5-14
材料
黑度
常用工业材料的黑度s
(5-87)
20
红砖
0.93
K;C1为
耐火砖
材料
钢板(氧化的)
200~600
0.8~0.9铜(氧化的)
温度/℃
黑度e
钢板(磨光的)
940~1100
0.8
铜(磨光的)
200~600
0.57~0.87
铸铁(氧化的)
200~600
0.55~0.61铝(氧化的)
0.64~0.78铝(磨光的)
200~600
0.03
寸,Eo也
银(磨光的)
225~575
0.11~0.19
,在常见
灰体的发射能力E(W·m2),可根据上述的E=E关于λ积分而得
200~6000.0390.057
0.012-0.03
高于4000
能很好地
E=S Exd-ef -)
式中,εCo为灰体的发射系数,以符号C表示,即
(5-89)
C=C0或C_E_E=
三、克希霍夫定律
CO EO EAO
(5-90)
克希霍夫定律确定物体的发射能力E与其吸收率A'之间的关系。
设有两平行壁I与Ⅱ,壁I为灰体,壁Ⅱ为黑体,且壁面大而距离很近。这样,从一个
T
壁面发射出来的能量可认为全部投射于另一壁面上,称为两无限大平行
平壁。以E1、A1和E。、A6分别表示壁面I、的发射能力和吸收率,
2
如图5-46所示。以单位时间单位壁面积为基准。由壁面1所发射的能
E1
实际物体,T
量E1投射于壁面Ⅱ表面上面被全部吸收;但由壁面所发射的能量E。
投射于壁面表面上时,只有一部分被吸收,即A1E。,而其余部分即
(1-A1)E被反射回去,仍落在壁面Ⅱ上而被完全吸收。若、Ⅱ两壁
Eo
面温度相等,即两壁面之间的辐射传热达到平衡时,壁面I所发射和吸Au Eo
物体和
收的能量必相等,即
(1-A)E
布
E1=A1E或=E
得
因具有E1和A1的壁面I可用任何壁面来替代,故上式可写成(5-91)
=Eo
Π
式(5-91)称为克希霍夫定律,它说明一切物体的发射能力与其吸图5-46克希霍夫
定律的推导
(5-88)
收率的比值均相等,且等于同温度下绝对黑体的发射能力,其值只与物
C为
体的温度有关。比较式(5-91)和式(5-90)可得出:A=e=E/E,即
定律,
在同一温度下,物体的吸收率和黑度在数值上是相等的。应当指出,和A在物理意义上并
不相同:表示灰体发射能力占黑体发射能力的分数;A'为外界投射来的辐射能可被物体吸
付能力
收的分数,只有在温度相同以及e与A随温度的变化皆可忽略时,e在数值上才与A相等。工业上常遇到的辐射传热,为两固体间的相互辐射,而这类固体,在热辐射中都可视为
体,两固体间由于辐射而进行热交换时,从一个物体表面发出的辐射能,只有一部分到达
四、两固体间的相互辐射
898/T,
物体
部分被
式中,C1-2为总发射系数,即C1-2=Co
1
+1-1
第五章传热191
必须
E1E2
这种热
是,在面积均为A的两无限大平行面间的辐射传热速率为
1+1-1
CAC2Co
(5-97)
下面将
式中Q1-2的单位为W。
Qn-C1-2A[()"-('门
(5-98)
的例
当两平行壁面间的距离与表面积相比不是很小时,从一个平面所发出的辐射能只有一部分到达另一平面上,则式(5-98)应改写成为如下更普遍的形式
47),
总能
Q-C1-pA[()"-()]
(5-99)
分即
中,为几何因子或角系数。角系数表示从一个表面辐射的总能量被另一表面所拦截的分
射的
,其数值与两表面的形状、大小、相互位置以及距离有关
一表面发射的全部能,必然接辐到一个或几个表面上去根据系数的定义。其和必为1,即
-92)
11+12+13+…=1
以两个无限大平行面1、2为例,由平面1发射的能量全部落在平面2上,这时角系数
(5-100)
=1,而对于平面1本身来说,由于发射的能量不能直接辐射到本表面的任一部分,所以=0,而φ12+φ11=1。同理,21=1,22=0,21+22=1。
(二)一物体被另一物体所包围时的辐射
一物体被另一物体所包围时的辐射是工程中常会遇到的情况,例如室内的散热体、加热中的被加热物体、同心圆球或无限长的同心圆筒之间的辐射等。在这类情况下式(5-99)中被包围体的角系数1=1,总发射系数为
Co
C1-2=
(5-101)
+(一)+(一)
式中,e1、e2分别为被包围物体和外围物体的黑度;A1、A2分别为被包围物体和外围物体的辐射面积;C1、C2分别为被包围物体和外围物体的发射系数。
于是
Q1--Ci-A[()-(门
(5-102)
式(5-102)可用于不同形状的表面之间的辐射,但要求被包围物体的表面1为平表面或
93)
另若图5-48(a)中表面2的温度T高于表面1的温度T1,则求Q1时可按下式计算凸表面,如图5-48(a)~(c)所示。
Q2-1=-Q1-2=-C1-2A1[()-()门
若外围物体可作为黑体,或被包围物体的辐射面积A1与外围物体的辐射面积A相比
4)
小,例如插入管路的温度计,则式(5-101)中的C1-2可简化为
C1-2=C1=∈1C0
(三)任意形状、大小并任意放置的两物体表面间的相互辐射
在这种情况下,如图5-49所示,仍可应用一般式(5-99),其中的总发射系数为(5-103)
5)
C1-2=E1e2Co
(5-104)
角系数为(见图5-49)
6)
g-A0 os a
192化工原理
dA
(2)
下,也等
n2
又
因A1=A
dA
(a)
(c)
图5-49任意放置的两物体
由表5-14
图5-48一物体被另一物体所包围时的辐射
表面间的相互辐射
式中,1、2为辐射线与辐射面的法线所组成的角度;A1、A2为两任意放置物体的辐射面
又铝板为
积;A为计算辐射传热采用的面积;r为两辐射面间的距离。
入式(a)
式(5-104)中的积分可用解析法或数值法求得。工程上为了使用方便,通常把角系数理求解的结果制成算图。本章只列出两平行平面间直接辐射传热的角系数算图(见图5-50),
0.816X
他情况可参阅传热学方面的专著。
解出
1.0
所以,放
0.8
0.6X
0.4
即放置铝
0.2
由以
0
高,可以
5
或
量还可以
五、
图5-50平行平面间直接辐射传热的角系数
气体
1一圆盘形;2-正方形;3一长方形(边长之比为2:1);4-长方形(狭长);
O2、N2
或边长(长方形用短的边长)或直径
辐射面间的距离
HCI、CO
力和吸收
【例5-21】有一高0.5m、宽1m的铸铁炉门,其表面温度为600℃。试求(1)由
与固
于炉门辐射而散失的热流量;(2)若在炉门前25mm外放置一块同等大小的铝板(已氧化)作为热屏,则散热热流量可降低多少?设室温为27℃。
内的辐射
有发射能
解(1)未用铝板隔热时,铸铁炉门为四周的壁面所包围,1=1;且A2>A1,故C1-2=1C0。查表5-14取铸铁的黑度e1=0.78,C1-2=0.78×5.669=4.42。由式(5-102)
换言之,
可求得炉门的辐射散热热流量为
蒸气各有
射与灰体
Q=4.42×1×0.5×1×
[(雪)'-(门]
其次
=2.21×(5808-81)=12660W
100
内进行的
这样,吸
图5-51
另一物体表面,而到达的这一部分能量又由于部分反射而不能全被吸收。同理,从另一物休190化工原理
表面反射回来的辐射能,也只有一部分回到原物体表面,而回到的这部分能量又有一部分
式中,C12为总发
反射和一部分被吸收,这种过程不断反复进行。因此,在计算两固体间的相互辐射时,必须考虑到两物体的吸收率和反射率、形状与大小,以及两者间的距离和相互位置。可见这种热于是,在面积均
两固体间辐射传热的结果,是将热能从温度较高的物体传递给温度较低的物体。下面将辐射的计算是很复杂的。
式中Q1-2的单位
分别讨论几种简单的情况。
当两平行壁
(一)两无限大平行灰体壁面之间的相互辐射
两平行灰体壁面间的相互辐射是最简单的情况,可用以作为分析和推导计算式的例分到达另一平面
子。两个面的温度、发射能力和吸收率分别为T1、E1、A1和T2、E2、A2(见图5-47),且T1>T2。对平面1来说,其本身的发射能力为E1,同时从平面2辐射到平面1的总能量为E2(即图中1、2两平面间自右至左各箭头所表示的能量的总和),其中一部分
式中,为几何
数,其数值与两
AE被平面1吸收,其余部分即(1-A1)E则被反射回去,因此从平面1辐射和反射的
任一表面发
能量之和E(即图中自左至右各箭头所表示能量的总和)应为
其和必为1,即
E=E1+(1-A1)E2
(5-92)
以两个无限
今
E2
P12=1,而对于
(1-A)E1
(1-A1)E2
11=0,而12
(二)一物
一物体被
(1-A)(1-A2)E1
(1-A)(1-A2)E2
炉中的被加热
(1-A)(1-A2)2E1
(1-A)2(1-A1)E2
中被包围体的
(1-A)2(1-A)2E
(1-A)2(1-A2)2E2
(1-A)3(1-A2)2E2
式中,ε1、E2
12
T
(a)
T2
的辐射面积;
(b)
于是
图5-47两平行灰体间的相互辐射
同样,对于平面2,本身的辐射能E2和反射的能量(1-A)E之和E
式(5-102
E2=E2+(1-A2)E
(5-93)
凸表面,如图
两平行壁面间单位时间单位面积的辐射传热量为此两壁面的辐射总能量之差,即
另若图5
91-2=E1-E2
由式(5-92)和式(5-93)解得E和E2后,代人上式得
E1A2-E2A
若外围物
91-2-A+A2-AA
(5-94)
很小,例如插
再以E1=C()、E2=e2Co()和A=e及A=e代入上式,整理后得
(三)任
-[(高)-(高)]
(5-95)
在这种情
EE
或写成
ae-c[()-()门
而角系数为
(5-96)




