蒸汽-燃气联合循环实例:北京京桥电站的效率计算
北京京桥电站与2013年投入使用,是一个蒸汽燃气联合循环的例子。我们将通过一些网络上公开的数据,对北京京桥电站的最大效率进行一个
北京京桥电站与2013年投入使用,是一个蒸汽燃气联合循环的例子。我们将通过一些网络上公开的数据,对北京京桥电站的最大效率进行一个估计的计算。
主要信息来源:
powermag网站-中国北京京桥电站SGT5-4000F | F-class Gas Turbine | Gas Turbines | Manufacturer | Siemens Energy Global主要结构的建立
由power网站的信息可以得到:

京桥电站是蒸汽-燃气联合电站,它包含两个燃气循环和一个蒸汽循环,为了简化,我们将两个燃气循环并为一个,我们将其抽象为布雷顿循环和兰金循环的组合。

在其兰金循环中,有三个涡轮:高压涡轮(HP),中压涡轮(IP)和低压涡轮(LP)。在最大功率时,三台涡轮机同时工作。
还有一些其他信息,不再贴图,直接提取:
布雷顿循环也就是燃气循环有两个SGT5-4000F(290 MW ISO)燃烧涡轮机,兰金循环也就是蒸汽循环两台三压热回收蒸汽发生器(HRSG),处于三个涡轮中间,设计工作在12.5 MPa,过热温度为545℃,再热温度为540℃,冷凝器的压力为0.4MPa,不使用低压涡轮时,出水温度为260℃。电站输出功率为838MW。
我们可以画出其结构示意图如下:
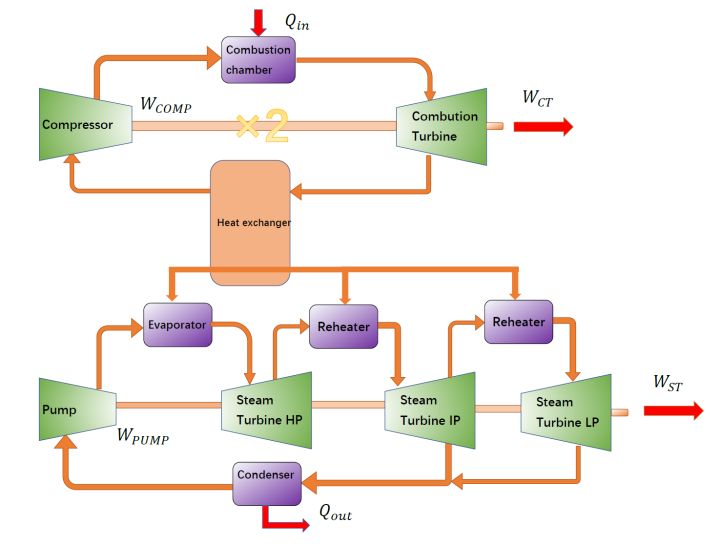
我们的目的是计算其效率,图中红色部分都是系统与外界之间的能量交换,那么总的效率有:

通过状态进行的计算
我们可以通过对状态的计算来帮助我们找到吸收的热量。
理想兰金循环的计算
我们将电站的蒸汽循环简化为理想的兰金循环。其T-S图如下:
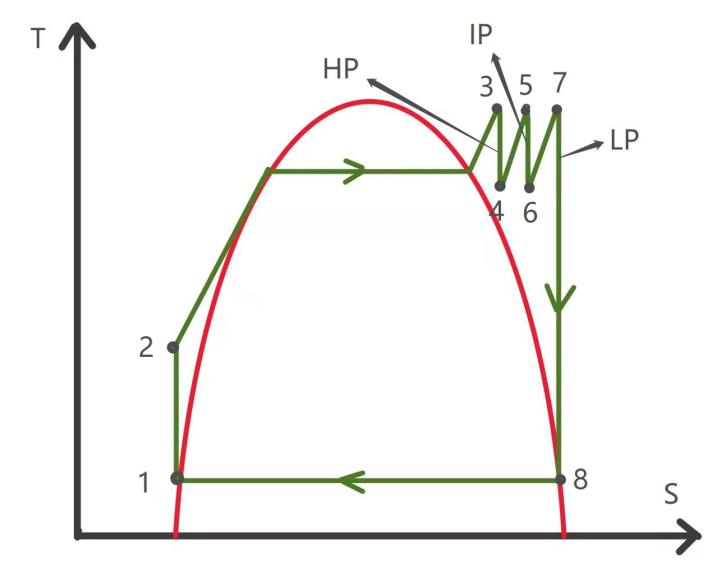
红色线为蒸汽饱和曲线
- 1-2为泵中的等熵压缩
- 2-3为锅炉中的等压吸热,包含过加热部分
- 3-4为高压涡轮中的等熵膨胀
- 4-5为再加热过程(HRSG)
- 5-6为中压涡轮中的等熵膨胀
- 6-7为再加热过程(HRSG)
- 7-8为低压涡轮中的等熵膨胀
- 8-1为冷凝器中的等压放热
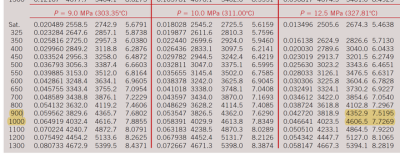
状态1的计算:
因为冷凝器的压力为0.4MPa,所以初始压力为0.4MPa,且状态1是在饱和曲线上的,所以我们可以得到状态1的熵与焓:
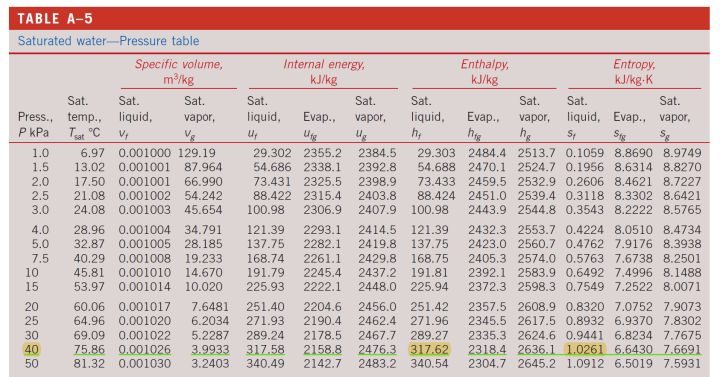
所以我们有状态1的信息:
状态2的计算:
1-2为等熵压缩,2-3为等压吸热,由此我们查表来确定状态2(过冷水)的信息:
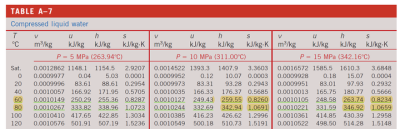
查表发现并没有给出 
可以看到 







所以再对一眼就能看出插值是 
我们就能得到状态2的信息:
状态3的计算:
状态3是加热完毕进入高压涡轮时的状态,鉴于已有HRSG的数据,那么我们这里就使用这个数据作为计算依据,即: 
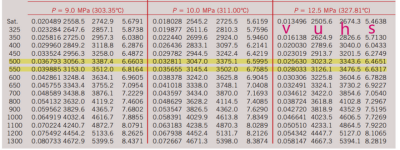
所以我们对温度插值有状态3的信息:
状态4的计算:
由书上可知,最佳的再加热压力为循环最大压力的四分之一

所以有: 
而3-4为等熵膨胀,则: 
同样进行查表(过热蒸汽)
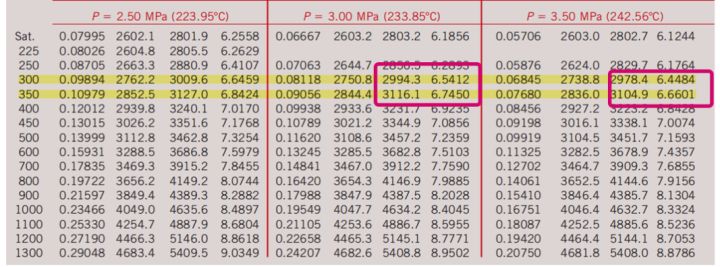






所以再对一眼就能看出插值是 
我们就能得到状态4的信息:
状态5的计算:
HSRG在12.5MPa工作,所以: 
与4类似进行查表:
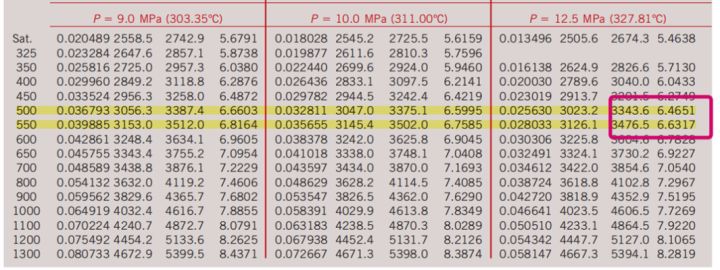
可以得到:


可得到状态5的信息:
状态6的计算:
5-6为中压涡轮中的等熵膨胀,后面接着进入HSRG,所以有:

同样查表进行计算:







再对压强进行插值可得:


所以有状态6的信息:
状态8的计算:
我们假设状态8也正好位于饱和曲线上(其实是没有其他数据没法算了,实际还有一定偏移)
那么 
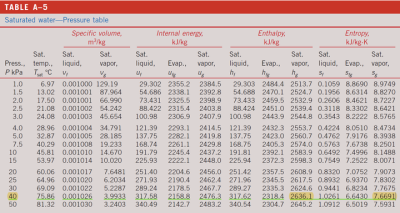
所以我们有状态8的信息:
状态7的计算:
7-8为等熵膨胀,那么: 


所以我们有了所有状态的信息:
| 状态 | P:MPa | T:℃ | h:kJ/kg | s:kJ.kg·K |
|---|---|---|---|---|
| 1 | 0.4 | 75.86 | 317.62 | 1.0261 |
| 2 | 12.5 | 76.585 | 333.27 | 1.0261 |
| 3 | 12.5 | 545 | 3463.21 | 6.615 |
| 4 | 3.125 | 323.42 | 3048.3 | 6.615 |
| 5 | 12.5 | 540 | 3396.76 | 6.53174 |
| 6 | 3.125 | 303.5 | 2998.875 | 6.53174 |
| 7 | 12.5 | 972.13 | 4535.8 | 7.6691 |
| 8 | 0.4 | 40 | 2636.1 | 7.6691 |
理想布雷顿循环的计算:
这部分信息主要来自西门子官网,
其T-S图如下:
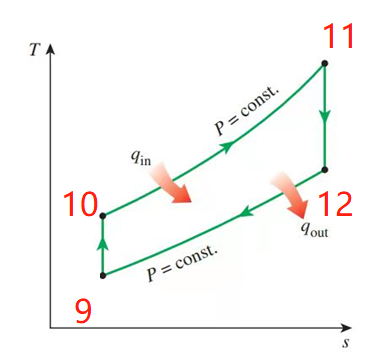
状态9的计算
我们使用标准冷空气假设,以此作为进气条件,那么有:

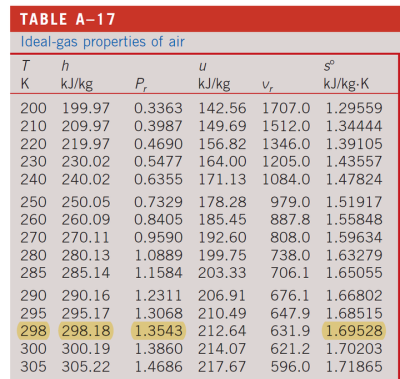
可以得到状态9的信息:
状态10的计算:
由西门子官网得到的信息:
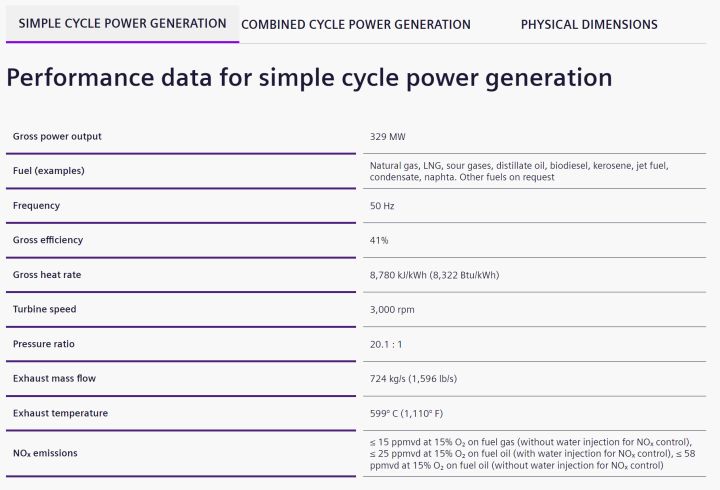
燃气机的压缩比为20.1:1,我们近似为20:1
所以我们有: 那么 
查表获取状态10信息:
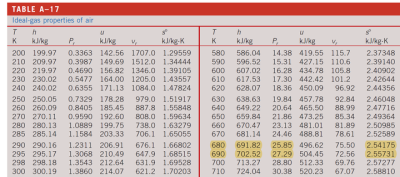
进行插值:


可以得到状态10的信息:
状态12的计算:
根据西门子的数据,出气温度约为600℃,即: 
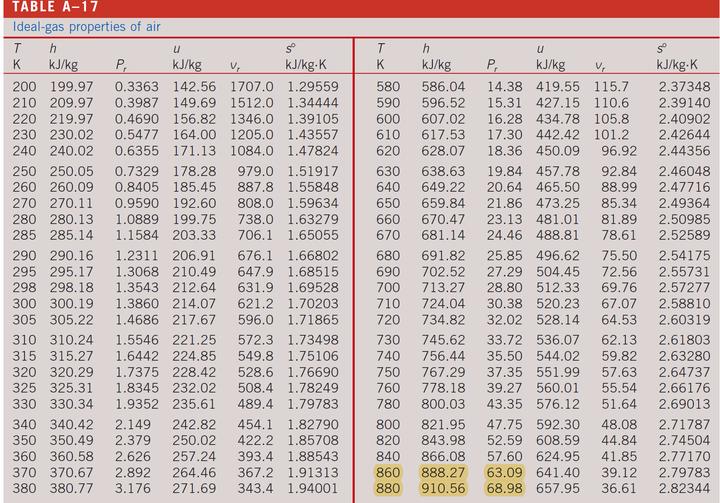


状态11的计算:
已知压缩比,那么 
查表:
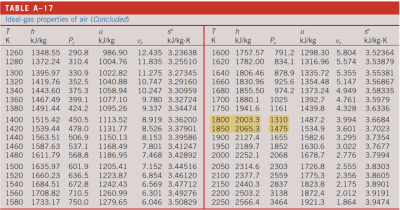


于是我们有布雷顿循环的所有状态:
| 状态 | T | Pr | h |
|---|---|---|---|
| 9 | 298K | 1.3543 | 298.18kJ/kg |
| 10 | 688.51K | 27.08 | 700.96kJ/kg |
| 11 | 1808.6K | 1338.4 | 2013.97kJ/kg |
| 12 | 873K | 66.92 | 902.7585kJ/kg |
理想状态下的效率:
那么我们已经有了所有信息:
兰金循环:
| 状态 | P:MPa | T:℃ | h:kJ/kg | s:kJ.kg·K |
|---|---|---|---|---|
| 1 | 0.4 | 75.86 | 317.62 | 1.0261 |
| 2 | 12.5 | 76.585 | 333.27 | 1.0261 |
| 3 | 12.5 | 545 | 3463.21 | 6.615 |
| 4 | 3.125 | 323.42 | 3048.3 | 6.615 |
| 5 | 12.5 | 540 | 3396.76 | 6.53174 |
| 6 | 3.125 | 303.5 | 2998.875 | 6.53174 |
| 7 | 12.5 | 972.13 | 4535.8 | 7.6691 |
| 8 | 0.4 | 40 | 2636.1 | 7.6691 |
布雷顿循环:
| 状态 | T K | Pr | h kJ/kg |
|---|---|---|---|
| 9 | 298 | 1.3543 | 298.18 |
| 10 | 688.51 | 27.08 | 700.96 |
| 11 | 1808.6 | 1338.4 | 2013.97 |
| 12 | 873 | 66.92 | 902.7585 |
所以我们有整个系统的输入输出信息:



而根据西门子官网和网站信息,我们可以得到两个循环的质量流动率:


所以我们有:


且我们可以计算出总输出功率为:

可以看出与838MW十分不相符
那么我们可以得到理想效率:

明显是偏大不符合实际的
使用等熵效率对实际效率的逼近
我们对各个等熵过程使用等熵效率进行对实际情况的逼近,我们这里认为等熵效率为80%,那么则有:



,


所以我们能得到:






所以我们重新计算整个系统的输入输出信息:



而根据西门子官网和网站信息,我们可以得到两个循环的质量流动率:


所以我们有:


且我们可以计算出总输出功率为:

与实际输出功率838MW比较相近
此时布雷顿循环中燃气涡轮的效率为:

与实际描述290MW比较相近
那么我们可以得到近似实际效率:

比较符合实际情况
通过输出输出直接计算:
既然我们之前已经得到:

那么吸热就只有布雷顿循环的吸热,我们可以通过布雷顿循环找出热量输入即可计算效率
我们正好有西门子官网燃气机的参数:
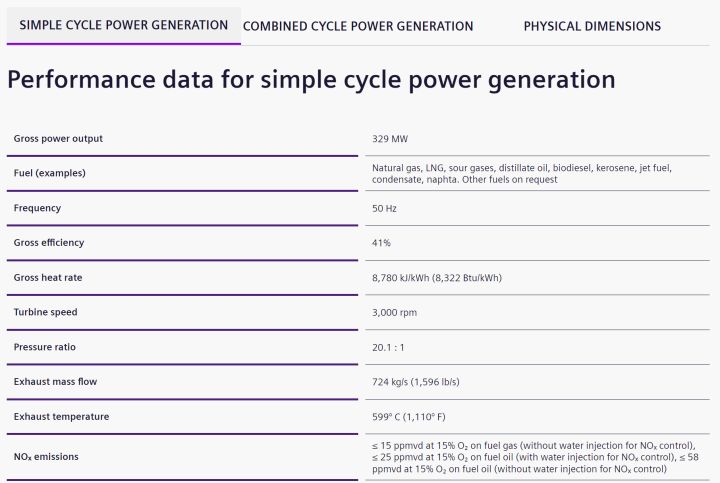
燃气机的效率为41%,而描述中燃气机的功率为290MW,与西门子官网不太一样,我们就使用描述中的功率
所以我们可以计算出吸热:


所以效率为:

与真实情况的对比:
通过描述,我们可以找到,京桥电站在不供热纯发电的情况下,可以达到59.5%的效率
我们通过状态计算出的效率只有49.08%,可能的原因有如下:
- 等熵效率:80%是一个给定的通常的值,可能以现在的技术手段,可以达到比80%更高的等熵效率
- 没有考虑其他提高效率的手段,比如布雷顿循环的再生,兰金循环在压缩阶段的冷却等
而通过涡轮效率计算出的效率为59.238%,是十分贴近给定的效率的
鸣谢
感谢Merle以及同小组的Lucie Ethan Jérémy Zachary,在projet中的讨论和努力,以及我们整个小组的不太正确的答案,为本文寻找一个比较正确的答案提供了参考和坚实的基础。同样感谢白嫖怪们的催更。












































