综合能源系统最优热力潮流(OTF)模型建立与Gurobi实现
1. 最优热力潮流的定义和最优电力潮流(OPF)类似,最优热力潮流(Optimal Thermal Flow,以下简称OTF)指当热力管网(包含冷网和热网)结构参数
1. 最优热力潮流的定义
和最优电力潮流(OPF)类似,最优热力潮流(Optimal Thermal Flow,以下简称OTF)指当热力管网(包含冷网和热网)结构参数和冷热负荷情况都给定的情况下,通过调节可利用的控制变量(分为质调节和量调节)来找到能满足所有运行约束条件的,并使系统的某一性能指标(如供能成本)达到最优值下的潮流分布。以我们所研究的case为例,其OTF问题可以描述为:节点1是包含了一台燃气锅炉和一台CHP机组的热源,节点4、5、6存在热力负荷且负荷值已知,如何调节热源的热出力功率,使得热力系统能够在满足末端负荷需求的前提下最小化运行成本。
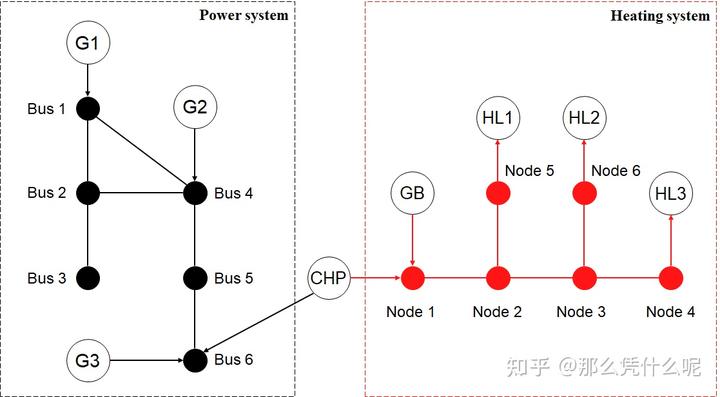
需要注意的是,和OPF相比,OTF有三个十分明显的区别,这也使得OTF模型的构建过程和OPF完全不同,概括如下:
- 控制变量不同。热力管网的控制方式主要可以分为质调节和量调节,前者指调节供水/回水温度,后者指调节供水流量。值得一提的是,目前国内热力管网大多采用质调节的控制方式;
- 管路数量不同。热力管网分为供水网络和回水网络,在计算时需要同时考虑供水管网和回水管网各节点和管段的能量守恒方程;
- 传输性质不同。热力管网传输能量的介质是水,水的传播速度远低于电的传播速度,且热力管网往往较长,因此需要考虑温度的延迟效应。同时,水在传输过程中会和环境产生热交换,造成温度的损耗效应。
2. OTF模型建立
本节考虑的OTF模型为质调节控制方法,即供回水流量保持定值,通过调节供回水温度的方式向末端负荷供能。模型同时考虑了温度的延迟效应和温度的损耗效应。OTF模型中的节点可以分为三类:热源节点、热负荷节点和中间节点。由于存在供水管道和回水管道,因此每个节点包含进口供水温度、出口供水温度、进口回水温度和出口回水温度四个控制变量。从约束条件的角度而言,每个节点具有供水和回水温度混合约束,这些方程同时考虑了水在传递过程中的延迟效应和损耗效应。此外,热源节点和热负荷节点还具有能量守恒约束。
2.1 供水/回水温度混合约束
根据能量守恒定律,任意一个节点供水/回水的出口温度乘出口总流量都必须等于所有入口温度和对应流量乘积的总和,如下式所示:

式中,




延迟效应采用简化的节点法进行建模,假设每个调度间隔对应的水量为一个质量块,如下图所示,则调度时刻 




式中, 



这个式子可以通过上图直接得到,非常直观且容易理解: 


接下来考虑温度的损耗效应,对其进行建模。热力管网在传输时会向周围环境散热,温度损耗和环境温度、传热系数等因素有关,可以由以下公式确定:

式中, 



2.2 热源节点和热负荷节点的能量守恒约束
对于热源节点和热负荷节点,其热出力/热负荷需要和供回水温差建立起能量守恒约束,如下式所示:


式中, 




3. OTF模型的代码实现
相比于OPF模型(其代码实现可见上一期专栏),OTF代码实现的主要区别包括:1. 需要同时考虑供水管网和回水管网;2. 上一个节点的出口参数(即温度)并不等于下一个节点的入口参数,需要考虑温度延迟和损耗;3. 不同类型的节点需要考虑的约束条件不同。
对于本专栏所研究的case,我们定义如下待优化变量,包括每个节点的冷却水出口温度和冷冻水出口温度和燃气锅炉的热功率,CHP机组的热功率由于可以由其电功率唯一确定因此忽略:
h_b = m.addVar(lb=b_list[0][2], ub=b_list[0][3], name='heating output of boiler')nts = m.addVars(n_node, vtype=GRB.CONTINUOUS, lb=lb_ts, ub=ub_ts, name='supply temperature from bus 1 to bus 6')ntr = m.addVars(n_node, vtype=GRB.CONTINUOUS, lb=lb_tr, ub=ub_tr, name='return temperature from bus 1 to bus 6')
代码的核心难点是如何快速高效地编写约束条件。这里仍然采用邻接矩阵的思想,首先分别生成供水管网矩阵、回水管网矩阵和节点类型矩阵,代码如下:
def generateMmatrix(n_node, br_sr):n M = np.zeros((n_node, n_node, 2))n for branch in br_sr:n M[branch[0].astype(int) - 1][branch[1].astype(int) - 1][0] = branch[2]n M[branch[0].astype(int) - 1][branch[1].astype(int) - 1][1] = exp(-branch[3] * branch[4] / (cp * 1000 * branch[2]))n return Mndef generateTypeArrays(node_list):n node_type1 = np.empty(shape=[0, 2])n node_type2 = np.empty(shape=[0, 2])n node_type3 = np.empty(shape=[0, 2])n for node in node_list:n if node[1] == 1:n node_type1 = np.append(node_type1, [node], axis=0)n elif node[1] == 2:n node_type2 = np.append(node_type2, [node], axis=0)n else:n node_type3 = np.append(node_type3, [node], axis=0)n return node_type1, node_type2, node_type3nnM_ts = generateMmatrix(n_node, br_s)nM_tr = generateMmatrix(n_node, br_r)nnode_type1, node_type2, node_type3 = generateTypeArrays(node_list)
简单说一下这两个方法都干了什么事:generateMmatrix方法根据传入的节点数量n_node和管路信息br_sr生成一个三维的M矩阵,若节点1到节点2之间存在一条支路,则在对应的行列中存入一个数组,第一个元素为管路流量,第二个元素为耗散效应的那一坨指数,这样方便直接调用计算;generateTypeArrays方法则是根据传入的节点类型生成三种类型的节点列表,type1是热源节点,type2是负荷节点,type3是中间节点。
之后,就可以用addConstrs方法一次性添加各节点的单个类型约束,代码如下:
# energy conservation equation for the nodes of type 1nm.addConstrs(cp / 1000 * sum(M_ts[node_type1[i][0].astype(int) - 1][j][0] for j in range(n_node)) * n (ts[node_type1[i][0].astype(int) - 1] - tr[node_type1[i][0].astype(int) - 1]) ==n h_chp_set[i] + h_b_set[i] for i in range(node_type1.shape[0]))n# energy conservation equation for the nodes of type 2nm.addConstrs(cp / 1000 * sum(M_ts[j][node_type2[i][0].astype(int) - 1][0] for j in range(n_node)) * n (ts[node_type2[i][0].astype(int) - 1] - tr[node_type2[i][0].astype(int) - 1]) ==n hl[i] for i in range(node_type2.shape[0]))n# supply temperature mixed equationnm.addConstrs(sum(M_ts[j][i][0] * ((ts[j] - t_amb) * M_ts[j][i][1] + t_amb) for j in range(n_node)) ==n sum(M_ts[j][i][0] for j in range(n_node)) * ts[i] for i in range(n_node))n# return temperature mixed equationnm.addConstrs(sum(M_tr[j][i][0] * ((tr[j] - t_amb) * M_tr[j][i][1] + t_amb) for j in range(n_node)) ==n sum(M_tr[j][i][0] for j in range(n_node)) * tr[i] for i in range(n_node))
前两个语句添加的是热源节点和热负荷节点的能量守恒约束,这里将两类节点分别保存在两个列表中,从而便于计算;后两个语句添加的是各节点供水管网和回水管网的温度混合约束,这里等式左边的节点入口温度原则上需要同时考虑延迟效应和耗散效应,代码中只考虑了耗散效应,原因如下:
当考虑温度延迟效应时,由于当前时刻的温度本质上取决于先前时刻的温度,这时优化问题会从时间无关的变为时间相关的,时间无关的优化问题在做优化时可以只把当前调度时刻的控制变量作为优化变量,而时间相关的优化问题需要同时将未来一段时间内所有控制变量作为优化变量,这会使优化问题的复杂度大大提升。同样会使优化问题变为时间相关的模型还有储能模型,因为储能装置的SOC取决于上一时刻的充放电状态。出于简单考虑,本case原型代码中忽略温度延迟效应(其实是我懒,本来想考虑一下但是需要修改的代码量太大)。这里给出这类问题的编程思路:很简单,把优化变量、约束条件、目标函数以及随时间变化的数据(末端负荷)等在原有基础上增加一个时间的维度。在代码实现上,就是在原有数组的基础上加一维,其他不变。
在构建了OPF模型和OTF模型后,我们终于可以写出这个问题的目标函数,代码如下:
obj = price_gas * (p_chp / effi_g2p + h_b / b_list[0][1]) + g_list[0][1] * p_g1 * p_g1 + g_list[0][2] * p_g1 + n g_list[1][1] * p_g2 * p_g2 + g_list[1][2] * p_g2 + g_list[2][1] * p_g3 * p_g3 + g_list[2][2] * p_g3nm.setObjective(obj, GRB.MINIMIZE)
目标函数包含两部分:第一部分是购气成本,天然气用于两部分,即驱动CHP机组和驱动燃气锅炉;第二部分是三台发电机的发电成本。至此,该case的优化问题已经完整的写出,可以执行运行获得最优的运行结果。
4. 完整代码
完整代码已经全部上传至Gitee,可直接下载跑来看一看,欢迎star和fork。一共有三个py文件:data、generate和main,优化运行的代码往往比较长,所以建议大家可以分成多个文件,既清晰也方便修改。我习惯于把case的所有数据都放在一个文件里,把操作函数放在一个文件里,主程序直接写gurobi代码,数据和函数可以直接调用,很方便。除了代码外,还附带了所测试系统的原始数据(testdata_CHPD.xls)。
5. 结语
不知不觉这个专栏终于结束了,总共耗时将近一个半月。随着这个专栏,我也顺带重新梳理了目前常用的模型,同时改进了一些自己之前写的代码,常用常新。祝大家都能按时、顺利毕业!




