拉瓦尔喷管
本文考虑的气体模型都采用理想气体。I.声速我们通常认为声波的周期远远小于气体局域平衡的弛豫时间。也就是说,在声音传播的过程中
本文考虑的气体模型都采用理想气体。
I.声速
我们通常认为声波的周期远远小于气体局域平衡的弛豫时间。也就是说,在声音传播的过程中气体满足绝热。
连续性定理: 


物态方程 


















II.气体的绝热流动
我们要处理的是在一维喷管中的运动。
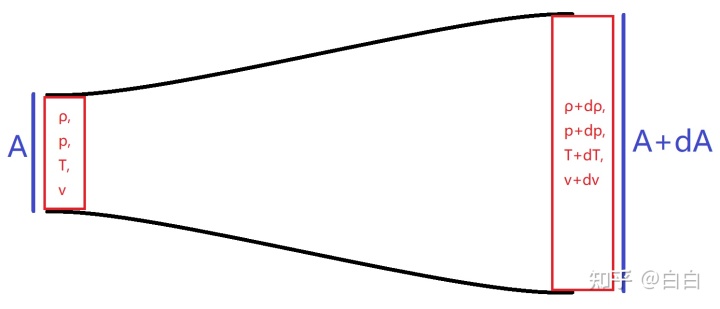
质量守恒: 
能量守恒(绝热): 

牛顿第二定律(其实是欧拉方程): 


如果我们沿着流线操作,也即人为地把 





我们可以利用能量守恒式子写出声速 










同时我们还可以看出,喷出的气体应当有一个最大的速度: 
我们看一下实际中的拉瓦尔喷管:
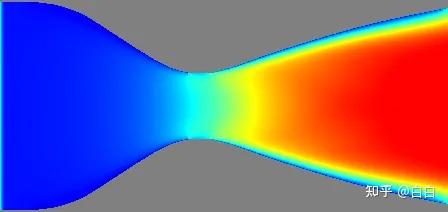
可以看出,我们的模型还是相当成功的。一个偏差在于我们只考虑了一维的流动;但这效应只在腰部明显。
有大佬做的拉瓦尔喷管在启动时候的数值解:
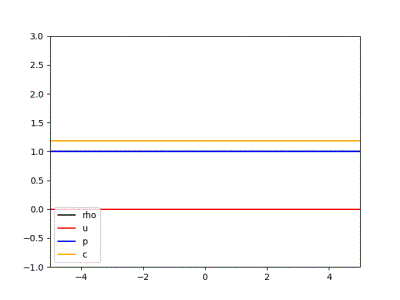
作者在这里不得不提一下计算过程中的错误:一开始我没有列出微元的动力学方程(欧拉方程),而寄希望与直接写出整体的受力方程。然而没有考虑到管壁对气体的压强,因而得到了速度维持不变的荒谬结论。这个错误显然是不应该的。
III.非设计状态下的拉瓦尔喷管
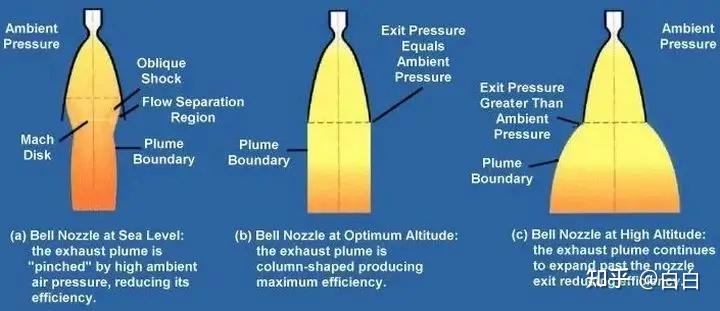
中间对应的就是设计状态;喷管口的压强就是外界压强,所以射流平行。
当外界压强不够大时,形如右图,成“欠膨胀”状态。
外界压强过大,形如左图,成“过膨胀”状态。此时在喷管口会形成一道斜激波,跨过激波后的气体压强略微升高。
若外界压强进一步增大,会在喷管口形成正激波,随着压强增大激波波面会逐渐向腰部靠近;直到达到腰部以后,不再能有超声速射流射出。





