散热量
传热学(第四版)例题专业资料讨论:从上表可以看出从i=3这一时刻起出现了这样的情况:个点温度随时间做忽高忽低的波动,并且波动弧度越来越
传热学(第四版)例题
专业资料



















































































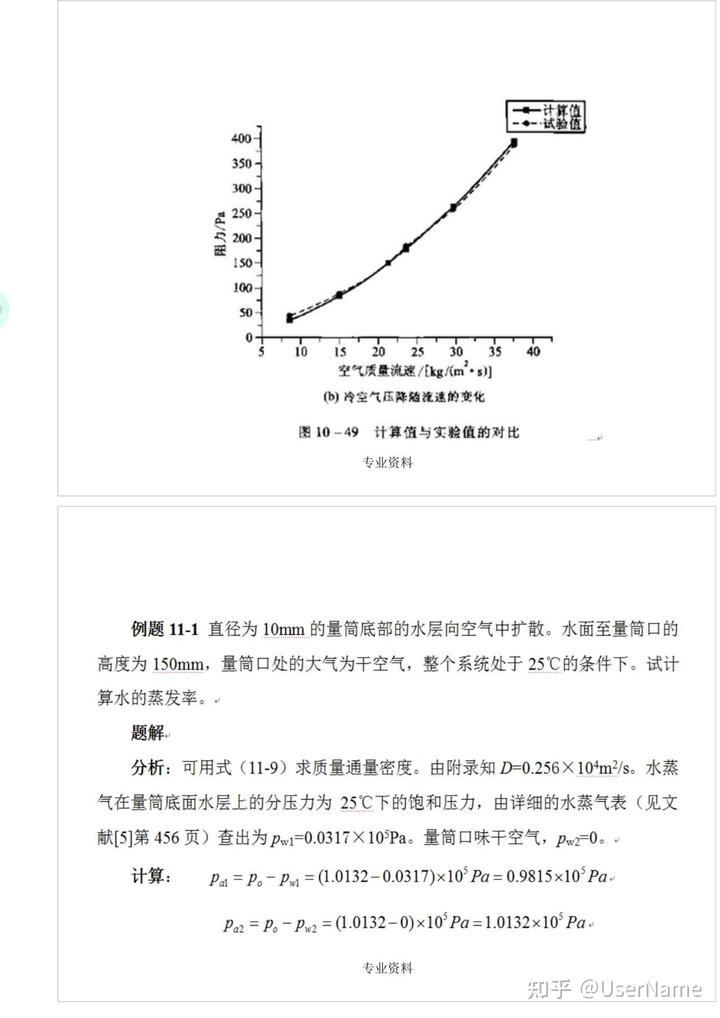









































讨论:从上表可以看出从i=3这一时刻起出现了这样的情况:个点温度随时间做忽高忽低的波动,并且波动弧度越来越大,某点温度越高反使其相继时刻的温度越低,例>3
这种想象是荒谬的,它违反了热力学第二定律,因为这意味着,在该时间间隔中从某一时刻起热量将自动的由低温点向高温点传递。数值计算中出现这种计算结果忽高忽低的波动现象,数学上称为不稳定性,这个例题表明,保证数值计算格式的稳定性是很重要的。
专业资料
例题4—4环肋肋效率计算用数值方法确定当r2/r=2,3,4
时环肋肋效率,其中r2,r1为环肋外半径及根圆半径(图4—12a)
假设(1)流体的表面传热系数为常数(2)一维稳态导热(3)肋片物性为常数(4)环肋顶端绝热
分析这是圆柱坐标中常物性一维稳态导热问题,导热微分方程式2—12可化简为
にボキー0 rdr dr
λ 将肋片上下表面的换热量折算成内热源:
Φ=2
(2πrdr)h(t-t,)
2
h(t-ty) (2πrdr)δ
8 t-tf Θ
引入无量纲过于温度
to-tf 及无量纲半径
R=
H
专业资料
可得这一导热问题的数学描写
d2Θ dΘ
-2㎡Θ=0 +
dR2 RdR R=R,Θ=1 R=R2,de
=0
dR 式中:
h 3/2
R1=r/H,R2=r2/H m=
x
VλA
由此可见,为了计算不同吓得肋效率需以m为参数。
计算:式4—23a是圆柱坐标中的无量纲一维稳态导热方程,式中的两个导数项分别用相应的中心差分格式代入,可得以下的差分方程式
-n+1-2-n++n
1n+1n-12㎡+n=0 AR2
R,
2AR
n=1,2,3.....N-1,Θ1=1,Θn=Θn-1 上式是肋顶绝热条件的一种数值处理方式
也可用高斯—赛德尔迭代法求解,获得Θn后再按定义计算肋效率
专业资料
ZAe
>AA
式中ΔA;为任意节点i所代表的微元体的换热表面积。,为该节点的无量纲过于温度。
表4—2列出了节点数N对肋效率η的影响。由表可见,为使在三位有效数字下的解稳定,应取N=36,此时可以认为已获得与网格无关的解。不同
肋效率随 m的变化列于下表
节点数对肋效率的影响
2/r
=2,m=2) N
8
16 20 36 64
100 7
0.26357 0.27082 0.27149 0.27238 0.27244
0.27249 环肋肋效率随
r2/r汲m的变化 0.1
0.5
1.0 1.5
2.0
2.5 2
0.991
0.813
0.542
0.37
0.272
0.213 3
0.989 0.781
0.490 0.321 0.23
0.177 4
0.987 0.756
0.454资料 0.29
0.204 0.154
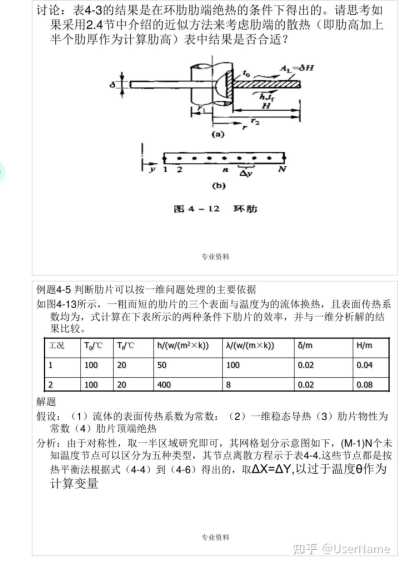
讨论:表4—3的结果是在环肋肋端绝热的条件下得出的。请思考如果采用2.4节中介绍的近似方法来考虑肋端的散热(即肋高加上半个肋厚作为计算肋高)表中结果是否合适?
=δH (a)
: 2
(q) 图4-12
环助
专业资料
例题4—5判断肋片可以按一维问题处理的主要依据
如图4—13所示,一粗而短的肋片的三个表面与温度为的流体换热,且表面传热系数均为,式计算在下表所示的两种条件下肋片的效率,并与一维分析解的结果比较。
工况
T/℃
h/(w/(㎡2xk))
N/(w/(mxk))
δ/m
H/m 0./1
1 100 20 50
100
0.02
0.04 2
100 20 400
8
0.02
0.08 解题
假设:(1)流体的表面传热系数为常数:(2)一维稳态导热(3)肋片物性为常数(4)肋片顶端绝热
分析:由于对称性,取一半区域研究即可,其网格划分示意图如下,(M—1)N个未知温度节点可以区分为五种类型,其节点离散方程示于表4—4.这些节点都是按热平衡法根据式(4—4)到(4—6)得出的,取ΔX=ΔY,以过于温度θ作为计算变量
专业资料
节点类别
下表变化范围
离散方程 ①
M=2,3...m-1, n=1
(θm-1.1 +0m+l.
+20m.2) 1
θ = - 三
4 ②
n=2,.....n-1 m=2,3...m-1,
1 (θm+h.n
0m-1.n
0m.n+l
0m.n-1) -=
+
+
+ θ
4 ③
m=2,3...m-1,n=N
0mN
(θm-1,N 1
0m+l.N +
20 +
m,N-1 4+
2Bi
Λ ③
m=M n=2,.....n-1
θM.n
(θM-1,n 1
0M+1,n
20M.n-1) +
+ 4+
2Bi
7 ④
m=M n=N
OM.N
(θM,N-1
+OM-1,N) 1
2+2Bi ④
m=M n=1
θM
(OM-1.1+OM.2) 1
1 专业资料
2+2Bi
D
在获得了过于温度场的分布后需按定义计算肋效率,对于本例肋效率的最终计算式为
Σ +
Σ M
I-N θ
θ 0.5(01.n+θM.)+
M,n m,n
n=2
n=2 n
[(M-1)+(N-1)]θ。
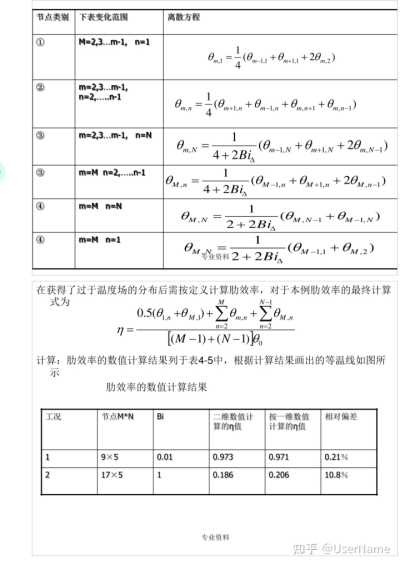
计算:肋效率的数值计算结果列于表4—5中,根据计算结果画出的等温线如图所示
肋效率的数值计算结果节点M*N
Bi
二维数值计
计算的η值 按一维数值
相对偏差 工况
算的η值 1
9x5
0.206
10.8% 0.01
0.973
0.971
0.21% 2
17x5
1
0.186 专业资料
对流
对流 28
H
④b
M h,fr
1 2 m
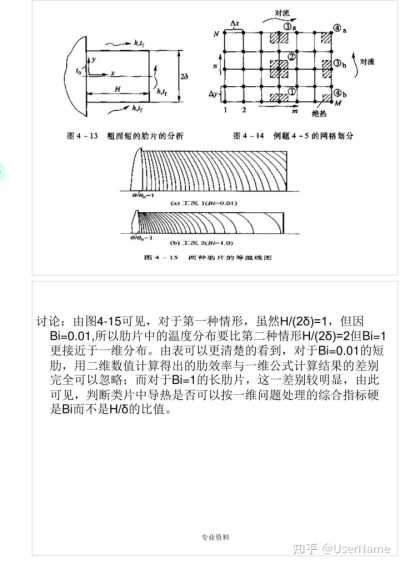
绝热 图4—13 粗而短的肋片的分析
图4-14
例题4—5的网格划分0/00=1
(a)工况1(Bi-0.01) 0/00=1
(b)工况2(Bi-1.0) 图4-15
两种肋片的等温线图
讨论:由图4—15可见,对于第一种情形,虽然H/(2δ)=1,但因
Bi=0.01,所以肋片中的温度分布要比第二种情形H/(2δ)=2但Bi=1更接近于一维分布。由表可以更清楚的看到,对于Bi=0.01的短肋,用二维数值计算得出的肋效率与一维公式计算结果的差别完全可以忽略;而对于Bi=1的长肋片,这一差别较明显,由此可见,判断类片中导热是否可以按一维问题处理的综合指标硬是Bi而不是H/δ的比值。
专业资料
例题4—6平板非稳态过程中的温度分布
用数值方法计算单侧受热的无限大平板的瞬态温度场。平板厚δ=0.1m
初始温度80℃,平板一侧被温度300℃的流体加热,另一侧绝热。设表面传热系数h=1163W/(㎡.K),材料的,λ=50w/(m·k)a=1,39x10-5㎡/s
题解
分析:这一问题可看作是厚度为28的平板两侧同时受流体加热的第三类边界条件下的非稳态导热问题,其控制方程式为式(3—14)—(3—16).将平板10等分,共11个节点,节点离散方程如式(4—17)—(4—20)所示(节点编号方法见图4—10)。计算计算结果采用等温线来表示。几个不同时刻平板中的温度分布示于图4—16.时间步长不同对计算结果的影响示于图4—17.图4—16的结果是按Δ,=0.18s
计算 得到的。
讨论(1)由图4—16可见,在
τ≤36s
的时间内,虽然平板受热侧已发生了显著的温度变化,但其绝热侧尚未受到界面上发生的热扰动的影响,因而在这一段时间内把厚=0.2m
的平板当做半无限大物体来处理应是一种合理的处理应是一种合理的处理方法。实际上,对于a=1.39x103㎡/s 半厚度为0.1m的半个平板,根据3.5节的讨论得其惰性时间为45s。
当t≥3min 后可以发现,平板中各点的温度有规则的随时间而上升,这就是非稳态导热的正规状态阶段。实际上,=3min
时已有 at
1.39x103㎡/sx180s F0=
82
专业(0.1m)
=0.25
·(3)图4—17表明,非稳态导热计算中的瞬时温度分布与时间步长的取值有关,但三种不同时间步长下解的差别在不断缩小。兼顾到计算的准确度与计算的工作量两方面的因素,本题以Aτ=0.18s
作为 计算步长。
专业资料
300
30min 24min
21 min
18min 15 min
15 min 0.
12 min t/℃
ΔΔr=1.8s
oΔr-0.18s 200
9 min
200
xΔ+=0.018s 6min
-0 3 min 001
100 00
0.1
0.0
0.1
0.0 x/m
w/x 图4—16 平板中温度的瞬态分布
图4-17
时间步长的影响 专业资料
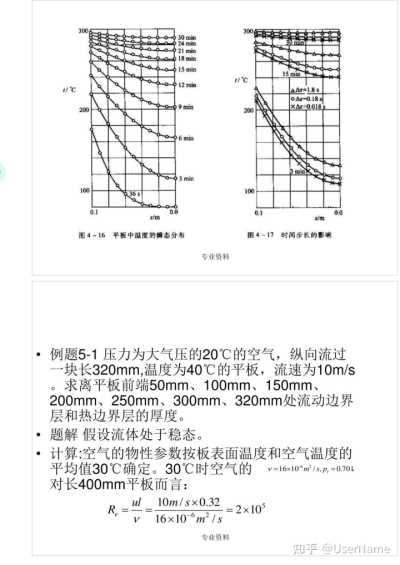
·例题5—1压力为大气压的20℃的空气,纵向流过一块长320mm,温度为40℃的平板,流速为10m/s。求离平板前端50mm、100mm、150mm、
200mm、250mm、300mm、320mm处流动边界 层和热边界层的厚度。
·题解 假设流体处于稳态。
·计算:空气的物性参数按板表面温度和空气温度的平均值30℃确定。30℃时空气的
v=16x10°㎡/s,p,=0.701 对长400mm平板而言:
ul
10m/sx0.32 R
=2x105 v
16x10-6㎡/s 专业资料
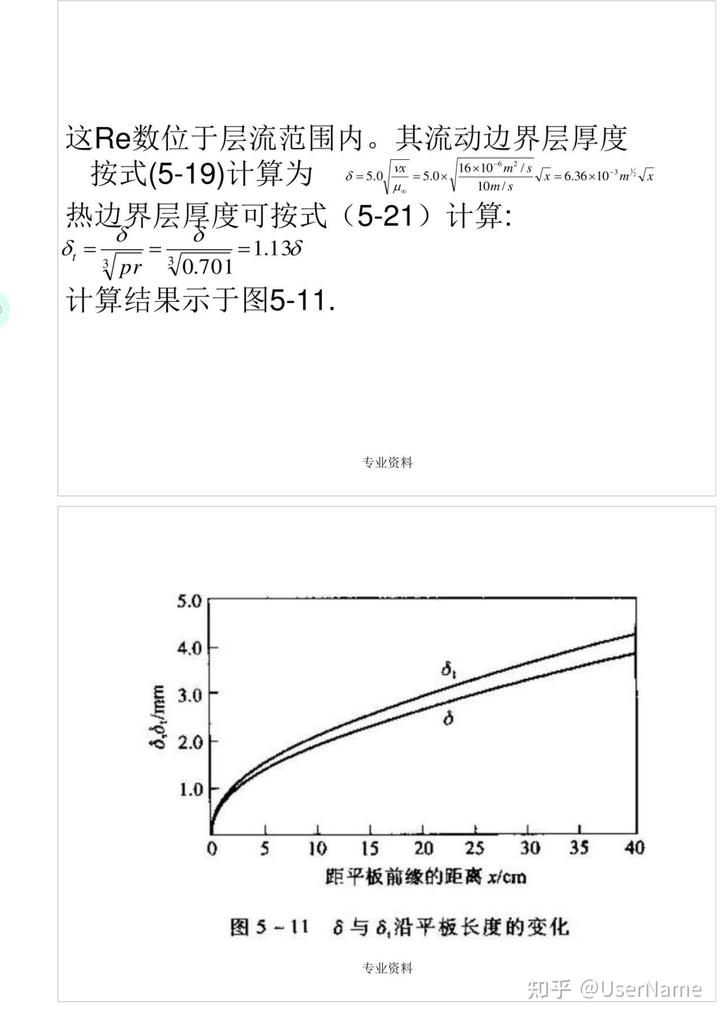
这Re数位于层流范围内。其流动边界层厚度按式(5—19)计算为
π2=5.0x 16x106㎡/s
x=6.36x10-3mx δ=5.0
10m/s 热边界层厚度可按式(5—21)计算:
δ
0
=1.138 0.701 d
计算结果示于图5—11.
专业资料 5.0
4.0
δ; 3.0
Q 2.0
1.0
T 0 5 10 15 20 25 30 35
40 距平板前缘的距离x/cm
图5—11 δ与δ,沿平板长度的变化
专业资料
8,8,/mnm
例题5—2上例中,如平板的宽度为1m,求平板与空气的换热量。
题解
假设(1)稳态;(2)不计平板的辐射散热。计算:先求平板的表面传热系数:
Nu=0.664RePr=0.664(2.0x10)2x0.701=263.7 λ
2.67x102w/(m·k)
x263.7=22.0w/(㎡·k) h=-Nu=
0.32m 1
式中
λ=2.67x102W/(m·K)
专业资料
是30℃时空气的导热系数。平板与空气的换热量为
Φ=hAΔt=22.0W/(㎡·K)x1mx0.32mx(40C-20°C)=140.8W
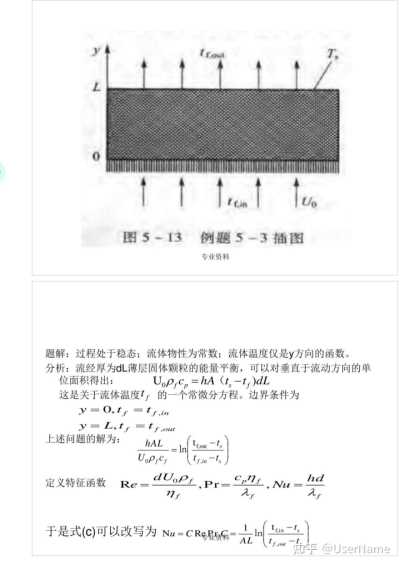
例题5—3离心力场作用下多孔介质物料层中的强制对流传热。如图5—13所示,温度为tf,in
流速为U
的流体,流经温度均匀的固体颗粒层,颗粒层厚度为L,温度为,t,>tf,in ,流体出口温度为ut
单位体积中的颗粒表面积为A,颗粒平均直径为d。试据能量平衡导出流体与颗粒间的平均表面传热系数h和流体的速度、热物理性质之间的关系式。
专业资料
7
0
Tuo ILin
图5-13
例题5-3插图 专业资料
题解:过程处于稳态;流体物性为常数;流体温度仅是y方向的函数。
分析:流经厚为dL薄层固体颗粒的能量平衡,可以对垂直于流动方向的单位面积得出:
UoPfCp=hA(ts-t,)dL
这是关于流体温度tf的一个常微分方程。边界条件为y=O,tf=tf,in
y=L,tf=tf.out 上述问题的解为:
hAL
trout-ts In UoPfCf
tf.in-ts
hd dUoP1,Pr=
cpn1,Nu=
λf 定义特征函数
Re
x nf
于是式(c)可以改写为
Nu=CRe=
1 trin u AL
例题5—4鱼雷表面温度的估计。
如图所示一鱼雷在10℃的海水中以15.4m/s的速度前进,受到的海水阻力为450N。假设鱼雷内的电子器件耗功为50kw,试确定鱼雷表面的平均温度。
计算:
鱼雷的表面积为
A=πdL=3.14x0.5mx5m=7.85㎡ 切应力为:
450N
=57.3N/㎡=57.3Pa 7.85㎡
10℃水的物性参数为Cp=4191J/(kg.K),Pr=9.52.有Chilton-Colburn公式可 得
h=
TCp57.3px419U/kg.K
=3480W/(㎡.k) UPr
15.4m/sx(9.52)■
鱼雷的平均表面温度可按生顿冷却公式计算:
Φ
50000V
+10℃=1.8℃+10℃=11.8C hA
3480W/㎡.kx7.85m
专业资料 弹头
燃料段
弹体尾部
尾部 50cm
6m
图5—14 例题5—4图示专业资料
例题5—5滚珠轴承中润滑油摩擦生热量的估算。
如图5—15所示,一滚珠轴承用高粘度的油来润滑。其中内圈运动,外圈静止。已知内外圈的速度差为1m/s,内外圈的间距为1mm。润滑油的动力粘度η=0.366Pa/s.试估算润滑油中由于摩擦而产生的热量。
假设:(1)润滑油为牛顿流体(2)轴承环形间隙中的流体可以按平行板间隙中的流动来近似处理如图(b)所示;(3)稳态过程。
计算:
=0.366P/sx
1m/s
=3.66x10W/m3 u=①
{m }
(금)4=(
0.001m 专业资料
内圈(转动) 润滑油
外圈(静止)
滚珠 (日)
滚珠(转动) 润滑油 L-
(b) 0- 0 Δu
外圈(静止)
图5—15 滚珠轴承中流体运动的简化模型
例题6-1
一换热设备的工作条件是:壁温 =80C 加热=80C
的空气 空气流速u=0.5m/s。
采用一个全盘缩小成原设备1/5的模型来研究它的换热情况。在模型中亦对空气加热,空气温度0C
壁面温度℃
试问模型中流速u'应为多大才能保证与原设备中的换热现象相似。题解:假设(1)稳态过程(2)被加热物体以80℃计算其物性,模拟气体以10℃计算其物性
计算:
非ー非 从而:
μ=/
取定性温度为流体温度与壁面温度的平均值t=(t+t,)/2
从附 录
v=23.13x106㎡/s,v=15.06x106㎡/s 查得
已知I/P'=5,于是模型中要求的流体速度u'为:
vl'(
0.5m/sx15.06x10㎡2/sx5 μ=μ
=1.63m/s 23.1Bx10-6㎡/s
1.4
例题6—2 用平均温度为50℃的空气来模拟平均温度为400℃的烟气的外掠管束的对流传热,模型中烟气流速在10—15m/s范围内变化。模拟采用与实物一样的管径,问模型中空气的流速应在多大范围内变化?假设:(1)稳态过程;(2)以50℃计算模拟气体(空气)的物性,以400℃计算实际工作气体(烟气)的物性。
计算:由附录知:400℃的烟气的
v=60.38x106㎡/s 50℃空气的95x106㎡/s
·为使模型与实物中Re数的变化范围相同,模型中空气流速应为
17.95x106㎡/s
x(10-15)m/s=(2.94~4.46)m/s 60.38x106㎡/s
·安排实验时模型中的空气流速应在这一范围内。
专业资料
例题6—3 水流过长l=5m、壁温均匀的直管时,
从
y=25.3℃
被加热到4.6℃ 管子的内径d=20mm,水在管内的流速为2/s,求表面传热系数。
计算:水的平均温度为
tj+t}
25.3℃+34.6C
=30℃ /1
2
2
以此为定性温度,从附录查的λ=0.618W/(m·K),v=0.805x10㎡/s,Pr,=5.42由此得
Re
2m/sx0.02m
4.97x10+>10 pr
Vf
0.805x106㎡/s
流动处于旺盛湍流区。采用式(6—15)求
Nu=0.023Re
0.8 Pr 0.4
=0.023x(4.97x10+)08x5.4204=258.5 )
M Nu=
0.618W/(m·K)
258.5=7988V/(m·K) x
d
0.02m
专业资料
·被加热水每秒钟的吸热量为
πd -rd=Φ
cp(t-t,) /
=995.7kg/m3x2m/sx
3.14x(0.02m)2
x4174//(kg·K)x(34.6℃-25.3℃) 4
=2.43x104W 先用下式计算壁温:
Φ tw=t+ hA
2.43x10+W =30℃+
℃=39.7
7988V/(㎡·K)x0.02mx3.14x5m
温差远小于20℃,在式(6—15)的适用范围,所求结果即为本题答案。
专业资料
·例题6—4在低风洞中用电加热圆管的方法来进行空气横掠水平放置圆管的对流换热实验。试验管置于风洞的两个侧壁上,暴漏在空气中的部分长100mm,外径为12mm.实验测得来流的t=15C 换热表面平均温度tw=125℃ ,功率P=40.5W.由于换热管表面的辐射及换热管两端通过风洞侧壁的导热,估计有15%的功率损失,使计算此时对流传热的表面传热系数。
Φ 计算:由牛顿冷却公式
h=
A(tw-t) 由已知得
Φ=0.58P=0.85x40.5W=34.43W 又
A=πdl=3.14x0.012mx0.1m=3.768x10-3㎡ 代入上式得
34.43W h
=83.1W(㎡·K) 3.768x10-3㎡x(125-15)℃
专业资料
例题 6—5 在一锅炉中,烟气横掠4排管组成的顺排管束。已知管外径d=60mms/d=2,S2/d=2,烟气平均温度tf=600°C,tw=120°C。 烟气通道最窄处平均流速u=8m/s。试求管束平均表面传热系数。
题解
分析:本题是直接给出了为采用茹卡乌斯卡斯公式所需的一切参数,可采用书末附表中平均烟气成分的物性进行计算。
专业资料
计算:
由书末查得
Pr}=0.62,Pr=0.686v=93.61x106㎡/s,λ=7.42x102W/(m.k)
·又
Re=
8m/sx0.06m
=5128
93.61x10-6㎡/s
·按表6—7中的关联式(6—31c)Nu,=0.27Re
0.63 P136 (Pr,/Pr)
0.25 f
=0.27x512863x0.620.36x
(0.62/0.686)025=48.2 λ
h=Nu=48.2x7.42x10-2w/(m·k)/0.06mm=59.6W/(㎡.k) d
·按表6—9,管排修正系数εn=0.91,故平均表面传热系数为h=Nu=59.6W/(㎡k)x0.91=54.2W/(㎡k)
专业资料
讨论:(1)与管内对流传热存在多个关联式的情形相类似,流体外掠管束也有不同的关联式,对同一个问题的计算结果相互间也有一定的差异。例如Grimson公式就是另外一个关联式(30,由于该式对一系列不同的S1、S2之值用表格方式给出了关联式的指数与系数,使用不便,同时仅适用于气体,因此本书不在推荐。
(2)作为例题,直接给出了为采用关联式所需的条件。但在工程实际中测定换热管子表面的平均温度是很困难的。
比较接近实际应用条件的计算模型是:测定了流体进、出管排处的平均温度,流体的流量,给出管排的几何条件。试分析在这种条件下如何应用表6—7至表6—9的结果来确定管束的平均表面传热系数。
专业资料
例题 6—6 室温为10℃的大房间中有一个
直径为15cm的烟筒,其竖直部分高1.5m,水平部分长15m。求烟筒的平均壁温为110℃时每小时的对流散热量。
题解
假设:整个烟筒由水平段与竖直段构成,不考虑相交部分的互相影响,分别按水平段与竖直段单独计算。
专业资料 计算:平均温度
=1/2(2+t)=1/(10℃+110℃)=60℃
由附录查得,60℃时空气的物性p=1.060kg/㎡3,cp=1.005kJ/(kg·K),
λ=0.029W/(m·K),v=18.97x10°㎡/s. (1)烟筒竖直部分的散热
Gr= gα,Δtl3
9.8m/s2x(1.5m)x(110-10)℃ v2
(18.97x10-6㎡/s)x(273+60)K
=2.76x1010
·由表6—10知为湍流,其
Nu=0.11(GrPr)3=0.11x(2.76x100x0.696)3=295 λ
·所以
0.029W/(m·K)
5.70W/(㎡.K) h=Nu
=295x - 1
1.5m
Φ1=πdlh(tw-t)=3.14x0.15mx1.5mx5.70W/(㎡.K)x100C=403W
专业资料
(2)烟筒水平部分的散热
Gr= gα,Δtl3
9.8m/s2x(0.15m)3x100℃
=2.76x107 (18.97x10-6㎡/s)x(273+60)K
由表6—10知为层流。于是
GrPr=2.76x107x0.696=1.92x10
1/4 Nu=0.48x
(2.76x10)
=31.8 0.029W/(m·K)
6.15W/(㎡.K) h=31.8x
0.15m
Φ2=3.14x0.15mx15mx6.15W/(㎡·K)x100°=4345W 烟筒的总散热量
Φc=Φ1+Φ2=(403+4345)W=4748V
专业资料
讨论:烟筒的总散热量还应包括辐射换热。取烟筒的发射率为0.85,周围环境温度为10℃,则烟筒的辐射换热量可近似地按式(1—9)估算:
Φ,=Aεσ(I-T4)
=(0.707+7.065)㎡x0.85x5.67W/(㎡·K+)x(3.834-2.83+)K4 =5660W
这里又一次看到,对这类表面温度不很高的物体,辐射换热量与自然对流换热量在数量级上是相当的。
专业资料
例题 6—7 一块宽0.1m、高0.18m的薄平
板竖直地置于温度为20℃的大房间中。平板通电加热,功率为100W。平板表面喷涂了反射率很高的涂层,试确定在此条件下平板的最高壁面温度。
题解
假设:因为表面反射率高,可以近似地认为热量全部通过自然对流散失,且热流密度均匀分布。
专业资料
分析:此题因为平板温度未知,而定性温度无法在计算前确定,需要采用迭代方式。即先假定一个定性温度,再通过计算加以检验和修正。
计算:先假定定性温度tm=200C,测得空气物性参数为
λ=0.0393W/(m·K),v=34.85x106㎡/s,P,=0.680
根据假设,得热流密度 q=100W/(0.1mx0.18mx2)=2778V/㎡。以板高为特征长度得
9.8㎡/sx
1
x(0.18m)+x2778V/㎡ (273+200)K
Gr
=1.226x10° 0.0393W/(m·K)x(34.85㎡/s)x10-12
相应的Nu数为
0.2 Nu,=0.60(GrP,)
=0.60x(1.226x10°x0.68)2=36.74 =
h Nu.λ
36.74x0.0393W/(m·K)
=8.02W/(㎡.K) x
0.18m 专业资料
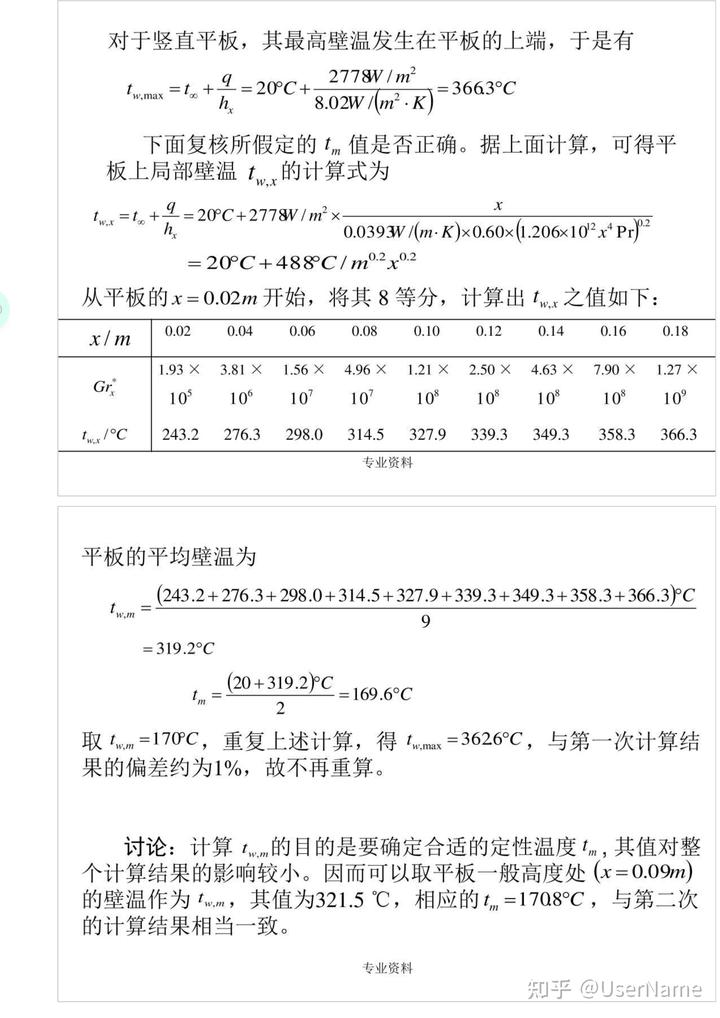
对于竖直平板,其最高壁温发生在平板的上端,于是有
2778V/㎡ b
tw,max=t+
h
=20℃+
8.02W/(㎡·K)
=366.3℃
下面复核所假定的tm值是否正确。据上面计算,可得平板上局部壁温t
的计算式为 x'M
tws=t+/2=20°C+2778V/㎡x h
0.0393/(m·K)x0.60x(1.206x102xPr)2 =20℃+488°C/m
0.2 0.2
x
从平板的x=0.02m开始,将其8等分,计算出t之值如下:x/m
0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
0.18 1.93x
3.81x 1.56x 4.96x 1.21x 2.50x 4.63x 7.90x
1.27x Gr
105 106 10 10 108 10 10 108
10° ■/℃
243.2 276.3 298.0 314.5 327.9 339.3 349.3 358.3
366.3 专业资料
平板的平均壁温为
(243.2+276.3+298.0+314.5+327.9+339.3+349.3+358.3+366.3)℃
9
=319.2℃
(20+319.2)℃
=169.6℃ 2
取twm=170C,重复上述计算,得twmax=3626℃,与第一次计算结果的偏差约为1%,故不再重算。
讨论:计算twm的目的是要确定合适的定性温度tm,其值对整个计算结果的影响较小。因而可以取平板一般高度处(x=0.09m)的壁温作为twm,其值为321.5℃,相应的tm=1708℃,与第二次的计算结果相当一致。
专业资料
例题 6—8 一个竖封闭空腔夹层,两壁是
边长为0.5m的方形壁,两壁间距为15mm,温度分别为100℃和40℃。试计算通过此空气夹层的自然对流传热量。
·题解
·分析:先计算Gr。之值,据此可以确定选用哪一个关联式。
专业资料
计算:定性温度为两壁的平均温度t
wl t
100℃+40℃ +
w2
=70℃ 2
2
从附录查得空气物性为:p=1.029kg/m3,v=20.02x106㎡/s,λ=0.0296W/(m·k),Pr=0.694.对于空气
1 1 α
=2.915x10-3K-1 T
343K m
专业资料
计算Grs:
9.8m/s2x2.915x10-3K-1x60℃x(15x10-3m)
=1.444x104 Grs=
(20.02x10-6㎡/s)
而H/δ=0.5m/0.015m=33.3,可按式(6—46)计算Nu,即
-1/9
0.5 Nu=0.197x(1.444x10*x0.694)4x
=1.335
0.015 所以
0.0296W/(m·K)
2.63W/(㎡·K) h=1.335x
0.015
自然对流传热量按牛顿冷却公式计算:
Φ=hAΔt=2.63W/(㎡.K)x0.25㎡x60℃=39.5W
专业资料
讨论:由于夹层厚度远小于平板的边长,可以把封闭腔夹层近似按两互相平行的无限大平板处理。于是,冷、热平板间的辐射传热量可按式(1—9)估计为
0.5mx.6W㎡(3-3.1K =138.3εW
取冷、热表面发射率为0.8,则Φ,=1107W。当要用实验方法来获得夹层中自然对流传热规律时,这样大的辐射传热量是不合适的。为了减少由于估算辐射传热的误差而对测定结果的影响,应减少表面的发射率。如果表面镀铬,设ε=0.05,则Φ,=6.92W,后者将使计算值的准确度显著提高。
专业资料
例题6-9
[48,49] 热线风速仪测速原理
。 热线风速仪探头的大致结构示
钨丝
D=20μm 于图6—26中。被测定速度的气流流
1
L=2mm
1.-40℃ 经钨丝的流动属于横掠单管的形式
。测定时对钨丝通电,设法使钨丝
空气 的平均温度保持不变,电流所产生
-支架 !_-20℃
的热量通过对流传热等散失。流速越大,保持钨丝为某个恒定温度所需的电流强度越大,通过预先的标定,就可以从电流强度获得被测定的流体速度。现在利用图中所示的数据从传热学计算角度来确定被测定
/=150mA 的流速。钨丝的温度是通过测定其
电阻而得出的,其值为0.4164 Ω
图6—26 热线风速仪示意图专业资料
题解
假设:电流所产生的热量全部通过对流散失,不计辐射和热丝端部导热的影响。
分析:这是流体外掠单管的强制对流,可选用式(6—28)及表6—5进行计算。但是,对本例流速是被求的量,因此需要根据牛顿冷却公式计算出表面传热系数,再据选定的关联式推算相应的流速。
计算:定性温度t=(40+20)°C/2=30℃C,相应的物性参数为
λ=0.0267W/(m·K),v=16x106㎡/s,Pr=0.701
电流的发热量为Φ=PR=(0.150A)2x0.41642=9.37x10—3W按牛顿冷却公式有
9.37x10-3W Φ
h=
A(tw-t)3.14x20x106mx2x103mx(40-20)℃
=3730W/(㎡.K) hd_3730W/(㎡.K)x20x106m
Nu=
=2.794 x
0.026W/(m·K)
专业资料
于是有2.794=CRe"。由于出现两个待定常数,需要采用试凑法。先假设Re数小于4,则由表6—5得C=0.989,n=0.33,由此推得Re=33.3。可见假设不正确。再设Re数处于4~40之间,则C=0.911n=0.385,得
Re 0.385
2.794
=3.452 0.911x0.7010333 Re=3.452/0.385
=25
这一数值与假定范围吻合,由此得气流速度为
Rev
25x16x106㎡/s
=20m/s n
d
20x10-6m
讨论:在热线风速仪测定技术中,一般采用Nu=A+BRe"这类形式的经验关联式。热线的Re数范围一般在2~40之间。有关热线风速仪的更多知识可参见文献【48】。
专业资料
例题6—10 地源冷量的利用。夏天一种节能型的家用空
调的方法是利用地下一定深处的温度低于环境温度的特点,将热空气送入地下深处的
田用 管道内冷却,然后送入房间循
冷空
热空气 环使用,如图6—27所示。已知
地下:
管理 ,送风管道内径D=400mm
风量=0.558m3/s,地下管道维持在壁温=18℃C,房间出风温度=25℃,要求进风
图6-27
夏天利用地源冷量的示意图温度=20℃C,管道的绝对粗
糙度=2.5mm
。试确定所需 管道的长度。
专业资料
题解
假设:(1)地源的热容量很大,管壁温度可以维持恒定;(2)对流传热处于充分发展的湍流阶段;(3)管道的转弯等不予考虑,均按直管计算。
计算:定性温度为tr=(20+25)℃C/2=22.5℃,查得物性参数为λ=0.026W/(m·K),v=15.3x106㎡/s,Pr=0.701 p=1.195kg/m3,cp=1005J/kg·K
截面平均流速
u=q(/4)=0.558m/s/3.14x(0.4m/4]=4.44m/s
4.44m/sx0.4m
Re=
=1.16x105 15.3x10-6㎡/s
专业资料 相对粗糙度为
Δ_2.5
1
Moody图上的阻力平方区要求ReD 400 160
数大于41600.5D/2Δ)085=4160x(160x0.5/2)0.85=4160x23=95685 显然,流动已经处于该区域,于是可以采用Nikurads公式计算阻力间:
1
1 f
=0.0325 1.74+21g
2/2)
1.74+21g
160
2 由Gnielinski 公式得
(f/8)(Re,-1000)Pr
(0.0325/8)x(1.16x105-1000)x0.701 Nu=
=395 1+12.7(f/8)05(P3-1)1+12.7x(0.0325/8)0.5x(0.701/3-1) Nu,λ_395x0.026W/(m·K)
25.8W/(㎡·K) hm
D
0.40m
专业资料
由空气侧的热平衡关系得总换热量为
Φ=pqc(t-t)=1.195kg/x0.558m/sx1005(kx(25-20)K =3350W
本题由于壁温为常壁温而且与流体温度比较接近,应该采用对数平均温差
(25-20)K Δt
=3.99K 25-18 In 20-18 Φ=hAΔtm=πDLhΔtm Φ
3350W L=
=25.9m πDhΔtm
3.14x0.4mx25.8W/(㎡.K)x3.99K
讨论:在空调工程中习惯采用冷冻吨来表示空调负荷,1冷冻吨的制冷量为3518W,所以上述空调负荷相当于1个冷冻吨,大概可供40㎡的房间空调之用。
专业资料
例题6—11 开缝翅片效率讨论(课堂/课外讨论用)
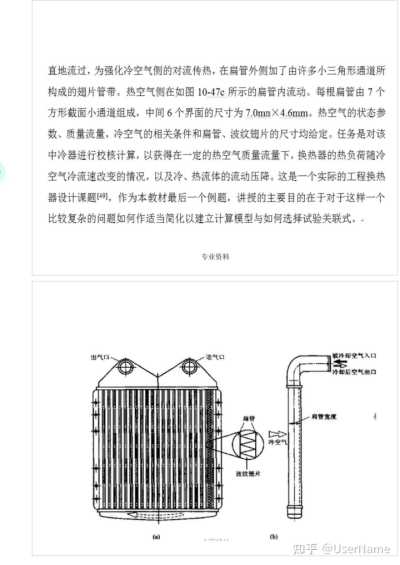
为了强化气体的对流传热,常常在气体侧换热表面上设置肋片或翅片,如图2—15所示。进一步的强化方法是在连续的翅片上开缝,从气流在翅片上边界层形成的角度,开缝可以切断边界层的连续发展,增加流体中的扰动,从而强化对流传热。图(6—28)示出了一种连续翅片与一种开缝翅片。开缝翅片是在连续翅片上冲出多条缝条制成的。这些缝条分别向两侧交替地突出,成为切断边界层与增加扰动的元件。
25.4 25.4
R3.6
R3.6
2 (a)连续直翅片
(b)开缝翅片 图6-28
连续直翅片与开缝翅片0.105
0.105
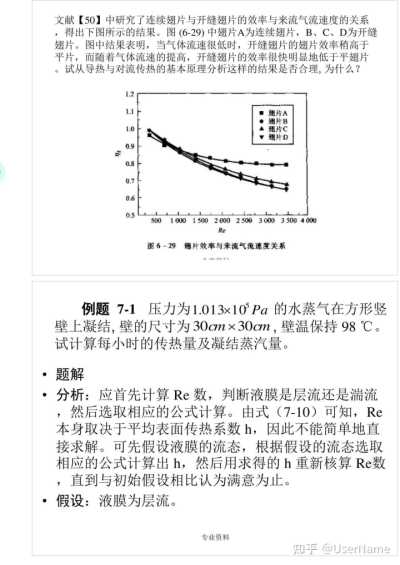
文献【50】中研究了连续翅片与开缝翅片的效率与来流气流速度的关系,得出下图所示的结果。图(6—29)中翅片A为连续翅片,B、C、D为开缝翅片。图中结果表明,当气体流速很低时,开缝翅片的翅片效率稍高于平片,而随着气体流速的提高,开缝翅片的效率很快明显地低于平翅片。试从导热与对流传热的基本原理分析这样的结果是否合理,为什么?
1.2
1.1
■翅片A
·翅片B 1.0
翅片C
翅片D 0.9
n_{2} 0.8 0.7 0.6 0.5 500
1000 1500 2000 2500 3000 3 500 4 000 Re
图6—29 翅片效率与来流气流速度关系
1--人
例题 7—1 压力为1.013x105Pa的水蒸气在方形竖壁上凝结,壁的尺寸为30cmx30cm,壁温保持98℃。试计算每小时的传热量及凝结蒸汽量。
·题解
·分析:应首先计算Re数,判断液膜是层流还是湍流,然后选取相应的公式计算。由式(7—10)可知,Re本身取决于平均表面传热系数h,因此不能简单地直接求解。可先假设液膜的流态,根据假设的流态选取相应的公式计算出h,然后用求得的h重新核算Re数,直到与初始假设相比认为满意为止。
·假设:液膜为层流。
专业资料
计算:根据
t,=100C,从附录查得r=2257kJ/kg。其 物性按液膜平均温度tm=(100C+98℃C)/2=99℃C从附录查取,得:
p=9584kg/m3,n=2.825x104Pa·s,λ=0.68W/(m·K) 选用层流液膜平均表面传热系数计算式(7—7)计算:
gp2x3r
h=1.13
nl(t,-tw)
1/4 9.8m/sx2257J/kgx(9584kg/m)x06sw(m. =1.13x
=1.57x10W/(㎡2.K)
专业资料 核算Re准则。按式(7—10)有
4hl(t,-tw) Re
nr
4x1.57x10*W/(㎡.K)x0.3mx2K
=59.1
2.257x10°J/kgx2.825x104Pa·s
说明原来假设液膜为层流成立。传热量按牛顿冷却公式计算:Φ=hA(t,-tw)=1.57x10*W/(㎡.K)x(0.3m)x2K
=2.83x103W
凝结蒸汽量为 Φ
2.83x103W 9m
1.25x10-3kg/s=4.50kg/h r
2.257x10°J/kg
专业资料
讨论:在已学习过的热量传递方式中,自然对流与凝结传热这两种方式的表面传热系数计算式显含有传热温差,自然对流层流时
h~Δt
14,而凝结液膜为层流时h~Δt—1/4。又由于凝结传热表面传热系数一般都很大,因而传热温差均比较小,因此,尽可能准确地确定温差对提高实验或计算结果的准确度都有重要意义。本例中如t改为99℃,则传热强度要提高 41%。
专业资料
例题7—2图7—14给出了压力为1.013x10Pa的饱和水的沸腾曲线,试据图估计实验表面与水间的Cm之值。
·题解
·分析:由压力为1.013x10Pa的饱和水的条件可以得出式(7—17)中的物性值,于是从图(7—14)上每一对Δt~q的数据就可以得出一个Cw之值。由于实验测定以及读取数据时不可避免的偏差,相应于不同Δt~q的Cw值会有所波动,取其平均作为代表值。这里仅对一个数据进行计算。
专业资料
计算:已知s=1,饱和温度
t=100℃。饱和水的物性从附录查得为:
cp=4.22kJ/(kg·K),Pr=1.75,p1=9584kg/m3, y=0.0589N/m,n=0.000283Pa·s,
而p,=0.589kg/m, r=2257kJ/kg
于是
[4220J/(kg·K)}x0.00028PPa·s
9.8m/s2x958.4kg/m3 b
x 2
(2257x10J/kg)x1.753
0.589kg/m3 =3.1x104W/(㎡.K)
从图7—14读得:q=4x10W/㎡时,Δt=10℃。于是C=31x10w/(㎡x)x(10c)73
=0.0092 4x105W/㎡
专业资料
讨论:该例题给出了如何由实验测定结果来确定不同固—液配对时系数c之值的方法。由于是从图中读取数值,因此仅能作为一种估算,实际确定c值时,应该以实验测定值为依据。幸好,计算得出的数值落在表7—1所列出的数值范围内。
专业资料
例题7—3 R12(氟利昂12)及R22由于其对大气臭氧层有破坏作用,已被国际社会规定禁止生产、使用或即将停止生产与使用。R134a是用以替代它们的一种新制冷剂。为了查明其传热性能,进行了大容器水平光管沸腾传热实验,并测得了表7—2所列的数据。试验条件是t,=5℃(p,=0.349MPa)。相对分子质量M,=102,临界压力p3=4.06MPa 试将库珀公式简化为h=Cq
0.67
的形式,并对计算值h及h。
的差别进行比较。 表7-2
例题 7—3的实验数据q/(W/㎡)
2.09x104 2.51x10 2.93x10 3.35x10+ 3.76x10 4.11x10+ 4.19x10+
4.61x10 h。
[w/(㎡·k)]
4058 4456 5 262 5 669 6059 6463 7 084
6 950 专业资料
题解
分析:应用式(7—18)时的一个不确定因素是Rp之值的选取。定性上,这个量与式(7—17)中的C相类似,取决于表面的条件。在没有实验测定值可以依据时,对商用管R,之值大约可取0.3~0.4 μm。
计算:式(7—18)可转化为h=[CM,
OSpm(-1gp,)
-0.55 0.67 =C1q
0.67 万
取R,=0.3μm,则m=0.2246。于是有C1=90W
/(㎡ 0.66 K)x102 205x 0.349 0.2246
0.349
-0.55 0.33
/
히 4.06
4.06 =4.96W0.33
/(m 0.66
K)
表面传热系数的计算值h及其偏离实测值h的百分数列于表7—3中。
专业资料
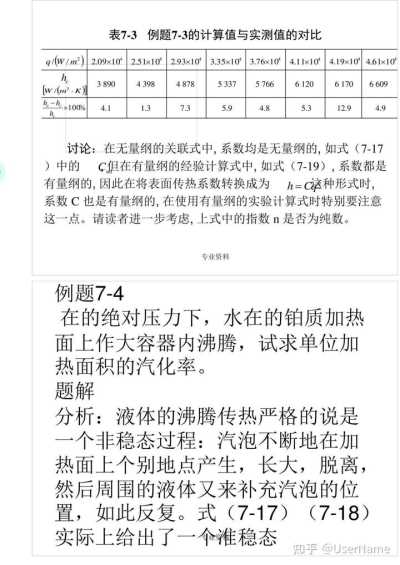
表7-3
例题7—3的计算值与实测值的对比q/(W/㎡)
2.09x10 2.51x10 2.93x10 3.35x10 3.76x10 4.11x10+ 4.19x104
4.61x10+ h。
[w/(㎡·k)] 3 890 4 398 4878 5337 5 766 6 120 6 170
6609 h.-hcx100%
5.9 4.8 5.3 12.9
4.9 4.1
1.3
7.3 h
讨论:在无量纲的关联式中,系数均是无量纲的,如式(7—17)中的
C,但在有量纲的经验计算式中,如式(7—19),系数都是有量纲的,因此在将表面传热系数转换成为
h=C这种形式时, 系数C也是有量纲的,在使用有量纲的实验计算式时特别要注意这一点。请读者进一步考虑,上式中的指数n是否为纯数。
专业资料 例题7-4
在的绝对压力下,水在的铂质加热面上作大容器内沸腾,试求单位加热面积的汽化率。
题解
分析:液体的沸腾传热严格的说是一个非稳态过程:汽泡不断地在加热面上个别地点产生,长大,脱离,然后周围的液体又来补充汽泡的位置,如此反复。式(7—17)(7—18)实际上给出了一个准稳态
过程的时间平均值。从本例下面的计算结果可以看出,由于汽泡的脱离,在加热面上相当于形成了一股连续的上升气流运动。
计算:壁面过热度,从图7—14知处于核态沸腾,因而可按式(7—17)求取q。
专业资料
从表7—1查的,对于水—铂组合。从附录查得,时水和水蒸气的物性为:Cpl=4.22kJ/(kg·K)
Pv=0.598kg/m3 P1=958.4kg/m3
r=2257kJ/kg -3
σ=58.9x10
N/m
Pr=1.75 n=0.2825x10-3Pa·s
专业资料
代入式(7—17)得
q=0.0002825Pa·sx2257x103 J/kg
x
1/2 9.8m/s2x(958.4kg/m3-0.598kg/m3)
X 0.0589N/m
3 4220J/(kg·K)x13.9℃
=3.79x105W/㎡ 0.013x2257x103J/kg
专业资料
单位加热面的汽化率为q_3.79x105W/㎡
0.168kg/(㎡·s) r 2257x103 J/kg
讨论:这是由汽泡的上升运动而形成的一股当量蒸汽流。正是由于这股气流所引起的对加热面附近液体的剧烈扰动,使沸腾传热的强烈程度远高于五项便的对流。如果以饱和蒸汽的密度来计算,这股质量流速相当于蒸汽以0.282m/的流速离开壁
专业资料
面向上运动。
例题7-5
试计算水在
1.01x10Pa 压力下沸腾时的临界热流密度,并与图7—14作比较。
题解
假设:加热面足够大,式(7—20)的应用条件满足。
计算:税基水蒸气的物性数值与例7—4相同。由式(7—20)得
专业资料
=0.149x2257x103J/kgx(0.598kg/m3)1/2 b
max
1/4 [9.8m/s2x(958.4-0.598)kg/m3x0.0594N/m] =126x104W/㎡
讨论:从图7—14读得9mm≈11.7x10W/㎡,与上述计算值的偏差为7.7%。在沸腾传热的计算中,这样的数值偏差已经算是很小了。
专业资料
例题7-6
水平铂线通电加热,在
1.01x105Pa 的水中产生稳定膜态沸腾。已
知w—ts=654℃C,导线直径1.27mm,求沸腾传热表面传热系数。
题解
分析:在稳定的膜态沸腾中,加热表面的总的表面传热系数由沸腾及辐射两部分组成。为确定辐射部分的大小,假定铂丝表面的发射率为
专业资料
0.9。 计算:
Pv,由n=(w+)/2=427℃确定。从附录查得:w=0.0505W/(m·K),n=0.0243x10-3Pa·s P1,r按t=100℃ 从附录查得:
P1=1.75,Cpl=4220J/(kg·K),σ=588.6x10~N/m 膜态沸腾传热表面传热系数按式(7—21)计算,得
专业资料
h=0.62x
{9.8m/s2x2275x103 J/kgx0.314kg/m3x(958.4kg/m3-0.314kg/m3)x
1/4 [0.0505W/(m.K)j
x[0.0243x10-3Pa·sx0.00127mx654C] x
=281W/(㎡2·K)
据壁面发射率ε=0.9,则由式(7-23)可得
0.9x5.67xW/(㎡2·K+)x[(10.27K)4-(3.73K)4] h,
654℃C =85.3W/(㎡·K)
专业资料 由式(7-22)得 h
4/3 =(281 4/3 +85.34/3
)W4/3/(㎡·K)
4/3 由此解得h=322.9W/(㎡·K)
此值小于简单叠加之值[366.3W/(㎡2·K)]讨论:此时热流密度为
q=322.9W/(㎡·K)x654·C=2.11x103W/㎡ 在同样的热流密度下,如果不发生膜态沸腾,而是处在旺盛沸腾区域内,则可据式(7—17)计算相应的表面传热系数。为此将该式转换成为计算表面传热系数的显示形式:
Cpl/r
0.67 h=
5人
0.33 1
σ
Pr C
IM
n.rVg(p1-pv)
将有关物性数值代入式(7—24),据表7-1取,得
专业资料 4220J/(kg·K)
h=
X 2257x103J/kg
0.67 b
0.33 1
588.6x104N/m
Pr' 0.013x
x
282.5x106kg/(m·s)x2257x103 J/kg9.m/s2x(958.4-0.958)kg/m3 =5.0W0.33/(m.66.K)q067
=5.0W0.33/(ma66.K)x(2.11x103W/㎡)067 =1.85x10+W/(㎡2·K)
可见,此时膜态沸腾的传热强度已经降低到旺盛核态沸腾的1/57。
专业资料
例题7-7
电热锅炉加热器长度及温壁计算。一台电热锅炉每小时生产75kg140℃的饱和蒸汽。采用外径为12mm的不锈钢管作为安置电热元件的外套。设计中取浸入水中的电热元件表面热流密度为7.75x104W/㎡。试确定需浸入水中的电热元件的总长度以及不锈钢管的平均表面温度。进入锅炉的给水温度为20℃。
题解 假设:
(1)按表7—1所示的机械抛光的不锈钢表面来计算;(2)电加热功率全部用来加热水;(3)水从20℃加热到140℃的过程按80℃时的比热容计算;(4)加热管在水中加热引起的沸腾属于大容器沸腾,但是因工艺上的原因加热管可能需要分层布置,这时上面的加热面将受到位于下面的加热面所产生汽泡的影
专业资料
响,
计算:140℃时饱和水的物性参数
为P1=926.2kg/m
Pv=1.965kg/m3 Cpl=4.287kJ/(kg·K)
n1=201.1x10-6Pa·s Pr1=1.26 σ=507.2x104N/m
r=2144.6kJ/kg 80℃C时的比热容为4175J/(kg·K)
将75kg,温度为20℃的水加热成140℃的饱和蒸汽需要的热量为
Q=75kgx[4175J/(kg·K)x(140-20)K+2144.6kJ/kg]=1.985x10J
1.985x103J 电热锅炉的热流量为
5.513x10+W 3600s
按设计的热流密度所需加热面积为Φ
5.513x104W
2 A=-
0.711m 7.75x10+W/㎡ b
所需浸入水中的长度为
2 A
0.711㎡ L=
18.7m
πd 3.14x0.012m
这样长的加热段必须分成几个弯头来布置,而弯头的多少取决于锅炉容器的长度。应用式(7—17)来计算加热面的平均壁温。该式写成温
专业资料
差的形式为
1/3
1/2
CwrPr ob
1 =1
[8(p,-p,)]27,r
Cpl
1/3 1/2
7.75x10+W/㎡2x(507.2x10+N/m)
X 1/2
9.8m/s2x(926.2-1.965)kg/㎡]
x201.1x106Pa·sx2144.6kJ/kg 0.013x2144.6kJ/kgx1.26
=6.17℃
4287J/(kg·K)
不锈钢管表面的平均温度为tw=ts+Δt=(140+6.18)℃=146.2℃
讨论:加热管长需18m,受到锅炉长度的限制以及工艺上的需要,
18m长度要分层布置。
这时上面的加热面将受到位于下面的加热面所产生的汽泡的影响。这里略去这种影响不计。由于6℃左右的加热温差使沸腾传热刚处于核态沸腾的开始阶段,汽泡不会很密集,这样的简化处理是可以接受的。
专业资料
例题7-8
竖直水平管排上平均凝结传热系数的保守估计。
如图7—28所示,在努塞尔理论分析8条假设的基础上,进一步假定上面管子的凝结液体平静地留到下面的管子上,不引起飞溅等现象。试导出在同一竖直排上第N根管子的平均凝结传热系数的计算式。
专业资料
1
1 g 1
x (a)
(c) (q)
图7-28
推导管排平均凝结传热系数的模型
题解
分析:在所假设的条件下,管排上液膜的形成与流下,可以看成是一张连续的液膜在被隔成N块离散的冷却面上流动。根据式(7-2)
λ1 grx3p1 2
71/4 1、
8
4n,(ts-tw)x
可知:h=Cx—1,对一定的传热温差与凝结条件,式中系数C为常数。
专业资料
图7—28c中每一根管子相当于高度为Δx一段传热面,因此有
Δx 4C -1/4 h=
Δx-1/4 =c/
x dx 0 3 C NAx 4C
-1/4 m-N
(NΔx)-1/4 =xp
x NAx J0
3 故有
1 N-M h
N1/4
讨论:得出上式的基本假定是:
(1) 液膜不飞溅;(2)液膜中的流动为层流。这种情况只有在凝结热负荷比较小时才能近似的成立.
例题8-1
试分别计算温度为2000K和
5800K的黑体的最大单色辐射力所对应的波长λm。
题解
分析:此题可直接应用Wien定律表示式(8—7)计算。
计算:
2.9x10-3m·K T=2000K
时, λm= 2000K
1.45x106m=1.45μm 2.9x10-3m·K
T=5800K 时, λm=专业资料
0.50x106m=0.50μm 5800K
讨论:上例的计算表明,在工业上的一般高温范围内(2000K)黑体辐射的最大光谱辐射力的波长位于红外线区段,而温度等于太阳表面温度(约5800K)的黑体辐射的最大光谱辐射力的波长则位于可见光区段。
专业资料
例题8-2
一黑体表面置于室温为27℃C的厂房中。试求在热平衡条件下黑体表面的辐射力。如果黑体加热到327℃C,它的辐射力又是多少?题解
分析:所谓热平衡就是指黑体表面温度与环境温度相同,即等于27℃。
专业资料
计算:按式(8—5),辐射力为
27+273
生/MGGtーと E=C.=.67W/(㎡k1)x
100 327C黑体的辐射力为
+또 c.(5/10) =5.67W/(㎡.k)x(
x+=7350W/㎡ //
Eb2
讨论:因为辐射力与热力学温度的四次方成正比,所以随着温度的升高辐射力急剧增大。虽然温度仅为的两倍,而辐射力之比却高达16倍。
专业资料
传热学
例题
2010/11/11
专业资料
例题1-1
一块厚度δ=50mm的平板,两侧表面分别维持在tw=300℃,tw2=100℃.试求下列条件下通过单位截面积的导热量:(1)材料为铜,λ=375W/(mk)
(2)材料为钢,λ=2.32W/(mk)
图1—1 通过平板的(3)材料为铬砖,
维导热 λ=36.4W/(mk)
(4)材料为硅藻土,λ=0.242W/(mk)
专业资料 解:
铜:
-t
300-100 q=x
w1 w2 -=375x
1.50x106W/㎡ 8
0.05 钢:
300-100 1
1- q=λ w1 w2 =36.4x
=1.46x105W/㎡ 8
0.05 鉻砖:
q=λ w1 -t
300-100
=9.28x103W/㎡ T
w2=2.32x 8
0.05 硅藻土砖:
-t
300-100 쓰
w2 =0.242x
=9.68x102W/㎡ x=b
8
0.05 专业资料
例题1-2
一根水平放置的蒸汽管道,其保温层外径d=583mm,外表面实测平均温度tw=48℃。空气温度t,=23℃,此时空气与管道外表面间的自然对流传热的表面传热系数h=3.42 w/(㎡k),保温层外表面的发射率ε=0.9。试求(1)此管道的散热必须考虑哪些热量传递方式;(2)计算每米长度管道的总散热量。
专业资料
解:此管道的散热有辐射传热和自然对流传热两种方式。
把管道每米长度上的散热量记为q1。
单位长度上的自然对流散热量为q1.c=πd·hΔt=πdh(tw-t) =3.14x0.583x3.42x(48-23) =156.5w/m
每米长度管子上的辐射换热量为
()3x=b
=274.7w/m 专业资料
于是每米长管道的总散热量为
q1=q1,c+91,r
=156.5W/m+274.7W/m =431.2W/m
专业资料
例题1-3
一块发射率ε=0.8的钢板,温度为27℃,试计算单位时间内钢板单位面积上所发出的辐射能。
解:钢板单位面积上所发出的辐射能为
q=8σT4=0.8x5.67x10-8W/(㎡·K4)x(27+273)4K4 =367.4W/㎡
专业资料
例题1-4
对一台氟利昂冷凝器的传热过程作初步测算得到以下数据:管内水的对流传热表面传热系数h=8700W/(㎡·K),管外氟利昂蒸气凝结换热 表面传数 h2=1800W/(㎡·K),换热管子壁厚δ=1.5mm。管子材料是导热系数 λ=383W/(m·k)的铜。试计算三个环节的热阻及冷凝器的总传热系数。欲增强传热应从哪个环节入手?
专业资料
解:三个环节单位面积热阻的计算分别如下:水测换热面积热阻:
1 1
=1.15x104㎡.K/W h 8700W/(㎡·K)
管壁导热面积热阻:
1.5x10-3m
=3.92x10-6㎡K/W 8
λ
383W/(m·K) 氟利昂蒸汽凝结面积热阻:1
1
=5.56x10㎡.K/W h2
1800W/(㎡2·K) 专业资料
于是冷凝器的总传热系数为:
1 k
1480㎡·K/W 1δ
1 +一+
h xh
氟利昂蒸汽侧的热阻在总热阻中占主要地位,它具有改变总热阻的最大能力。因此,要增强冷凝器的传热,应先从冷凝器侧入手,并设法降低这一环节的热阻值。
专业资料
例题1-5
计算夏天与冬天站立在同为25℃的房间内的人体与环境间的换热量。站立的人体与空气间的自然对流换热表面传热系数取为2.6,人体衣着与皮肤的表面温度取为30℃,表面发射率为0.95。夏天室内墙面温度取为26℃,冬天取为10℃。
专业资料
解:换热面积
A=(3.13x0.25x1.75+3.14x0.252/4)mm=1.42㎡ 人体冬天的总换热量:
Φ winter
=hA(tm1-ty)+εAσ(TM-)
=18.5W+154W=172.5W 人体夏天的总换热量:
=hA(tm-t)+εA(T ① summer
=18.5W+33.4W=51.9W
同一室温下,冬天人体的散热是夏天的3倍多,怪不得冬天会觉得冷,而夏天则由于不能及时散热而感到热。
专业资料
例题2-1
一锅炉炉墙采用密度为300kg/m的水泥珍珠岩制作,壁厚 δ=120mm 已知内壁温度
11=600外壁温 度t2=50℃,试求每平方米炉墙每小时的热损失。解:为求平均导热系数 ,先算出材料的平均温度
λ
500℃+50℃ t
=275℃ 2
于是
λ=(0.0651+0.000105x275)W/(m·K) =(0.0651+0.0289)W/(m·K) =0.0940W/(m·K)
专业资料
代入得每平方米炉墙的热损失为λ
0.0940W/(m·K) (1-1)
x(500℃-50℃) =b
0.120m =353W/㎡
专业资料
例题2-2
一台锅炉的炉墙由三层材料叠合组成。最里面是耐火粘土砖,厚115mm;中间是B级硅藻土砖,厚125mm;最外层为石棉板,厚70mm。已知炉墙内、外表面温度分别为495℃和60℃,试求每平方米炉墙每小时的热损失及耐火砖与硅藻土砖分界面上的温度。
专业资料
解:δ1=115mm δ2=125mm δ3=70mm 经过几次迭代,得出三层材料的导热系数为3=1.12W/(m·K),1=0.116W/(m·K),3=0.116W/(m·K) 代入得每平方米炉墙每小时的热损失为
11-14
435
W/㎡=244W/㎡ b
82 δ3
1.78 's
十 十 3
λ2 ■3
将此q值代入,求出耐火粘土砖与B级硅藻土砖分界面的温度为
0.115m t2=1-q
A/2=495°C-244W/㎡
x
=470℃ 1.12W/(m·K) 专业资料
例题2-3
已知钢板、水垢及灰垢的导热系数46.4W/(m·K)1.16W/(m·K)及0.116W/(m·K),试比较厚1mm钢板、 水垢及灰垢的面积热阻。
解:平板的面积导热热阻R4=8/λ
故有 钢板
RA
1x10-3m
2.16x10-5㎡·K/W 46.4W/(m·K)
水垢
1x10-3m R
=8.62x104㎡.K/W 人
1.16W/(m·K) 灰垢
RA
1x10-3m
=8.62x10-3㎡.K/W 0.116W/(m·K)
专业资料
例题2-4
在一个建筑物中,有如图2—11的结构。钢柱直径d=30mm,长度L=300mm,材料导热系数为λ=50W/(m·K),其两个端面分别维持在60℃与20℃,四周为建筑保温材料。计算通过钢柱的导热量。
解:
3.14x0.032㎡ (60-20)K Φ=λA
π/5=50W/(m·K)
x 4
0.3m =3.27W
专业资料
图2-11
习题2-4插图 专业资料
例题2-5
为了减少热损失和保证安全工作条件,在外径为133mm的蒸汽管道外覆盖保温层。蒸汽管道外表面温度为400℃。按电厂安全操作规定,保温材料外侧温度不得超过50℃。如果采用水泥珍珠岩制品作保温材料,并把每米长管道热损失
Φ/l控制在465W/m之下,问保温层厚度应为多少毫米?
专业资料
解:为求平均导热系数λ,先算出材料的平均温度
400℃+50℃
=225℃ 2
从附录7查得导热系数为
=0.0651+0.000105
=0.065+0.000105x225 {
다。 W/(m·K)
λ=0.0887W/(m·K)
因为d1=133mm是已知的,要约定保温层厚度δ,须先求得
d2,将式(2——31)改写成
2πλ ('p/p)u
(1-t2) / Ф 专业资料
即
2πλ In{d2}
(t1-t2)+In{d,}m Φ
/ 于是
In{d2}
2πx0.087
x(400-50)+ln0.133 465
=0.419-2.02=-1.601
d2=0.202m 保温层厚度为
8=d2-d1
0.202m-0.133m
=34mm 2
2 专业资料
例题2-6
压气机设备的储气筒里的空气温度用一支插入装油的铁套管中的玻璃水银温度计来测量,如图2—17所示。已知温度计的读数为100℃,储气筒与温度计套管连接处的温度为t0=50℃,套管高H=140mm、壁厚δ=1mm、管材导热系数λ=58.2W/(m·K),套管外表面的表面传热系数h=29.1W/(㎡·K)。试分析:(1)温度计的读数能否准确的代表被测地点处的空气温度?(2)如果不能,分析其误差有多大?
专业资料
15
H
图2-17
温度计套管
专业资料 据式(2——40)有
to-tf tH-tf
ch(mH) 归并整理得
tHch(mH)-t0 tf
ch(mH)-1
本例中,换热周长P=πd,套管截面积A=πdδ。于是,mH的值可按定义求出,即
mH= hP H= h H=
29.1W/(㎡·K)
x0.14m=3.13 VλA
Vλδ
V58.2W/(m·K)x0.001m 由数学手册查出ch3.13=11.5。代入
计算得 1
100℃x11.5-50℃C
104.7℃C 11.5-1
专业资料
例题2-7
为了强化换热,在外径为25mm的管子上装有铝制矩形剖片的环肋,肋高H=15mm,
厚δ=1.0mm。肋基温度为170℃,周围流体温度为25℃.设铝的导热系数λ=200W/(m·K),肋面的表面传热系数h=130,试计算每片肋的散热量。
专业资料
解:采用图2—20的效率曲线计算:
8
H'=H+-
=15mm+0.5mm=15.5mm 2
25mm =12.5mm 11
2
r2=r+H=12.5mm+15.5mm=28.0mm r2
28.0mm
=2.24 ri
12.5mm
A1=δ(-r)=0.001mx(0.028m-0.0125m)=1.55x10-5㎡ 1/2
130W/(㎡.K)
1/2 3/2
二 H22/1)
(0.0155m)
x20aw)(m.k)x1.55x105㎡ =0.396
专业资料
从图2—20查得ηf=0.82。
如果整个肋面处于肋基温度,一个肋片两面的散热量为①0=2π(㎡2-2)(to-t)
=2πx
[(0.028m)2-(0.0125m)]x130W/(㎡2·K)x(170C-25℃) =74.3W
每一个肋片的实际散热量Φ为Φ。与肋效率η的乘积,即Φ=74.3Wx0.82=60.9W
专业资料
例题2-8
图2—24示出了平板式太阳能集热器的一种简单的吸热板结构。吸热板面向太阳的一面涂有一层对太阳辐射吸收比很高的材料,吸热板的背面设置了一组平行的管子,其内通以冷却水以吸收太阳辐射,管子之间则充满绝热材料。吸热板的正面在接受太阳辐射的时同时受到环境的冷却,设净吸收的太阳辐射为q,表面传热系数为h,空气温度为t,管子与吸热板结合处的温度为,试写出确定吸热板中温度分布的数学描写并求解之。
专业资料
图2—24 平板式太阳能集热器吸热板
专业资料
推导:肋片的导热微分方程与边界条件为d2t
Φ =0式(h) + dx λ
s dt x=0,t=t;x=
=0 -
2 dx
现在进一步导出式b)中源项Φ的表达式。仿照前面的分析可以写出
hP(t-to)+q,P
m(1-10-/1)式(k) Φ
A。 代入式(h)得
(4/--)=/
专业资料
为使式(k)成为齐次方程,定义θ=t—t
qr
。于是得 h
d2t =㎡θ dx
S
dθ x=0,θ=θ0;x=
=0
2 dx
式(2—39)显然就是这一问题的解,而只要将其中的H用s/2来代替即可,此处不再列出。
2m0(/)
chm(x-/2) -mx
x +e
e 0
θ=θ
=θ 0
2m(1/2)
ch(m.s/2) 1+e
专业资料
例题2—9图2—27a给出了核反应堆中=原料元件散热的一个放大的筒型。该模型是一个三层平板组成的大平壁,中间为δ,=14mm的染料层,两侧均为δ2=6mm的铝板,层间接触良好。燃料层有p=1.5x0 W/ms的内热源
V
= =35w/(m*k)铝板中无内热源其
=100w/(m*k)表面受到温度t=150℃的高压水冷却表面传热系数h=3500w/(m2*k)不及计接触热阻,试确定稳定工况下染料层的最高温度,燃料层与铝板的界面温度及铝板的表
面温度并定性画出简化模型中的温度分布
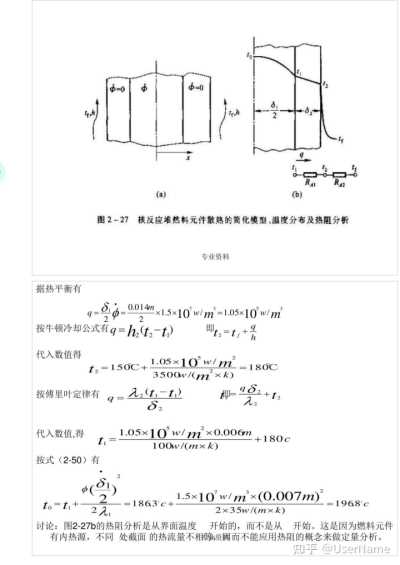
分析;由于对成性,只要研究半个模型即可。燃料元件的最高温度必发生在其中心线上(X=0处)记为界面温度及为铝板表面温度计为在稳态工况下燃料元件所发生的热量必全部散失到流过铝板表面的冷却水中,而且从界面到冷却水所传递的热流量均相同,顾可定性的画出截面上的温度分布及从界面到冷却水的热阻如图2—27b所示。图中为铝板的导热热阻,为表
面对流传热热阻,为从燃料元件进入铝板的热流密度
假设(1)一维稳态导热(2)不计接触热阻(3)内热源强度为常数计算
,据热平衡有
专业资料
Φ
Φ=0 0-Φ
RA2 (a)
(9) 图2-27
核反应堆然料元件散热的简化模型、温度分布及热阻分析
专业资料
据热平衡有
0.014m 9=0/20
10w/㎡=1.05x10^w/m x1.5x
2 按牛顿冷却公式有
q=h2(t2-t,)
即t2=t x 万
h 代入数值得
2 t2=150C+
1.05x
10°w/m
=180C 3500w/(㎡xk)
1+gb 按傅里叶定律有
λ2(t,-t1)
即 b
x2 8
2
2 代入数值,得
1.05x
<10°w/m
x0.006m
+180c t1
100w/(mxk) 按式(2-50)有
(0/1)
10'w/㎡x(0.007m)
2 1.5x
to=t1
186.3°+
=196.8℃ +
2λ
2x35w/(mxk)
讨论:图2—27b的热阻分析是从界面温度 开始的,而不是从 开始。这是因为燃料元件有内热源,不同 处截面的热流量不相等资因而不能应用热阻的概念来做定量分析。
例题2—10 如图2—29所示铀燃料充装于锆锡合金制成的圆管中,管子内外径分别为=8.25mm与d=9.27mm 管子呈正方形布置,管间距为17.5mm铀棒产生功率为。管束之间有温度为的冷却水流过冷却水与管子外表面的表面传热系数为。管子内壁与铀棒之间的接触热阻相当于增加了表面传热系数为的一个传递环节,试确定稳态过程中铀棒的最高温度
分析:本题只有在确定了铀棒的外表面温度后才能应用上面的分析解,在稳态过程中,从铀棒散出的热量通过接触热阻层,锆锡合金管传到冷却水中。由铀棒外表面散出的热量与相应总热阻的乘积可得出铀棒表面温度与冷却水温度之间的差值。由于锆锡合金以及铀棒的导热系数与温度与关,因此是非线性问题,需采用迭代方法计算。假设(1)稳态有内热源的导热;(2)4根铀棒导热情况一样,计算其中1根即可;(3)一维导热,计算对单位长度铀棒进行
计算:每米长度铀棒外表面的散热量为3.14
x1=8.37x
10°w/m
x(8.25x 10
)2x1m=46700w xφ=Φ
-x !p
4 铀棒外表面温度为
1
In(ro/r)
1 Tu=T,+ø(
2πr.h,x1m
2πλ
x1m 2πr;hx1m 1
In(0.485m/0.413m)
1 =400k+46700vx
2πx0.00413nx6000w/(mxk)
2λ
2πx0.00485nx10000v/(mxk) 人分
=400k+46700vx(0.00642+0.00149+0.00328k/w=923k
专业资料
先假定锆锡合金管子的平均温度为600k则入2n=17.2w/(m·k),代入上式得
T■=400k+46700vx(0.00642=0.00149)+0.00328k/w=923k
至此可以应用公式(2—52)计算铀棒的最高温度。因此需假设铀棒的平均温度,这里取为1500看,λu=2.6w/(m·k)于是有:
Tmax=T+
фr2
8.73x10w/m3x0.00413㎡ =923k+
=2355k 4λ
4x2.6w/(m*k)
现在需要检验所嘉定的温度是否合适,锆锡合金管的平均壁温为
0.0032+0.00149/2
Truben=400k+(923k-400k)x
=588k
0.00642+0.00149+0.00328
此值与600k相当接近,可以认为假设有效,铀棒的平均温度为
923k+2355k
イ
=1639k un
2
此值与1500k相差较远,有必要进行修正。按这一温度入u=2.6w/(m·k)计算得
8.73x103w/m3x0.00413㎡ T
=923k+
专业资料
=2412k max
4x2.5w/(m*k)
讨论;由于铀棒导热系数只给出两位有效数字,因此没有必要做进一步的迭代,对于有内热源的实心圆柱.球的导热问题,稳态时外表面上的导热量等于内热源功率的总和,需要分析求解的仅是温度分布
8.25mm
图2—29 例题2—10附图
例题2—11一根直径为250mm的输送水蒸气的管道用成型的保温材料来包覆,构成截面外形尺寸为500mmx500mm的隔热层。设蒸汽的平均温度为200℃,保温层外表面温度为60℃,保温材料的导热系数为0.1w/(m·k).管道长2米,试计算该管道的散热量。
专业资料
假设:(1)稳态常物性导热;(2)水蒸气与管道之间的换热阻力以及管壁的导热阻力远小于保温层的导热阻力,因而可以认为管道外表面温度即为水蒸气的平均温度。
计算;采用形状因子法来计算,所研究的对象如表2—2中第6栏所示,据已知条件有
2x3.14x2m
=16.3m 0.05m
1n(1.08x
0.25m
ф=λs(t1-t2)=0.1w/(w*k)x16.3mx(200C-60C)=228w
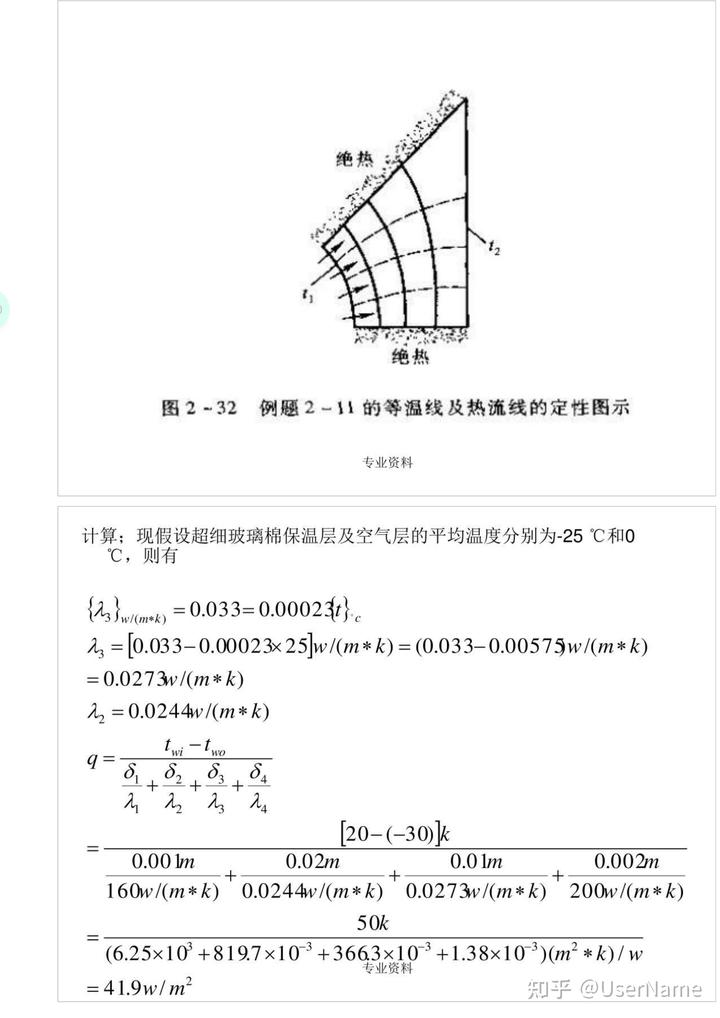
讨论:形状因子s是有量纲的物理量,其单位为米,对于所研究的问题,利用对称性可以对八分之一区域定性画出等温线与热流线如图
专业资料
绝热
绝热
图2—32 例题2—11的等温线及热流线的定性图示
专业资料
计算;现假设超细玻璃棉保温层及空气层的平均温度分别为—25℃和0℃,则有
{x3} w/(m*k)
=0.033=0.00023t}
x3=[0.033-0.00023x25]w/(m*k)=(0.033-0.00575)w/(m*k) =0.0273w/(m*k)
x2=0.0244w/(m*k) twi-t
O.1 b
8182+83 84 M 4
[20-(-30)]k 0.001m
0.02m
0.01m
0.002m 160w/(m*k) 0.0244w/(m*k)
0.0273w/(m*k)
200w/(m*k) 50k
(6.25x103+8197x10-3+3663x10-3+1.38x10-3)(㎡*k)/w
专业资料
=41.9w/㎡
由上面计算可见,内壁与蒙皮的热阻不到总热阻的1%,因而验算平均温度时可认为其温度分别为20℃及—30℃,空气层及超细玻璃棉保温层的平均温度为:
t3m=(20-41.9x0.8197/2)C=(20-17.2)C=2.8C
t2m=(-30+41.9x0.3663/2)C=(-30+7.7)C=-22.3C 上述两个温度与假定值很接近,计算有效。
在上述内外壁温下要使热损失减少一半,各层的平均温度会有所变化。近似的仍以上述数据进行估算。则可得:
Q wi wO O
69 0
を
を λ3
24 b
1 w0 δ1
S2_84) δ3=λ3(
λ4 と
を
b =0.0273w/(m*k)
50
(6.25+819.7+1.38)x10
㎡
*k/w 20.75
=0.0273w/(m*k)x(2.41-0.827)㎡*k/w=0.0432m
讨论(1)飞机座舱散热量是由舱内乘客以及飞机空调系统供给的热量来平衡的
业资料
,
在设计时为安全起见,可以认为均由空调系统所提供:(2)单从导热系数看,空气层的值比超细玻璃棉还小,但是要进一步减小散热损失,不能用加厚空气夹层的方法:这会导致夹层的自然对流,使散热量增加
例题2—13带肋片晶体管的冷却。
如图2—34a所示,有一直径d1=4mm,高H=6mm的晶体管,其外表面套着带纵向肋片的铝圈,铝圈的厚度为1mm,导热系数为
200w/(m·k).,铝圈与肋片系整体制造而成,肋片的高度与晶体管相同,肋片厚度均匀δ=0.7mm.铝圈与晶体管之间存在接触热阻,其值为RA.ct=10—3m2xk/w.平均温度为20℃的空气流过晶体管,表面传热系数为25w/(m2·k).运行中的晶体管的外表面温度维持为80℃,确定此时晶体管的功耗。
假设:(1)略去从晶体管顶上与底面的散热量不计:(2)一维稳态导热,肋片按等截面直肋看待,肋片顶端按绝热考虑,采用增加半个肋片厚的方法来计算导热量:(3)不计辐射换热。
分析:从晶体管表面温度t1到流体温度t,导热阻力网络如图所示,其中从肋片根部温度to到流体温度tt之间的两个并联的热阻分别是从根部向四周的散热阻力与从肋片的散热阻力。
品体管
有纵向肋的铝
(8)
R1 (q)
图2—34 带散热肋片的晶体管及导热网络
专业资料
计算:四个环节的总面积热阻如下:
RAct
103㎡*k/w
=13.3k/w =y
A
πx0.004x0.006㎡ 铝圈导热热阻
Ra=
In(d2-d,)
In(3/2)
=0.054k/w 2πλH
2πx200w/(m*k)x0.006m 等截面直肋的导热量为
φ=λA(to-t,)mth(mH)=(λAhp)2(to-t,)th(mH)
肋片的特性也可以用热阻来表示,这个概念对于用热阻网络来分析问题特别有用。根据热阻的基本定义,由上式可得通过等截面直肋的导热阻力为
to-t
1 =
Ø
(xAhp)2th(mH) hx2(H+S)
25w/(㎡*k)x2x(0.006+0.0007)m 心
非
λ(Hxδ)
200w/(m*k)x0.006x0.0007㎡ =(
25w/(㎡*k)*0.0134n
1/2
=20m 200w/(m*k)x4.2x10°㎡
mH=20m-1x(0.01+0.0007)m=0.207
(λAhp)1/2=(200w/(m*k)x4.2x106㎡x25w/(㎡*k)x0.0134n)12 =0.0168v/k
专业资料 th(mH)=th(0.207)=0.204
1
故有
R
0.204x0.0168v/k
=292k/w 12个肋片的热阻力为
R 291 f
w/k=24.3k/w Rj(12)
12
12 肋片根部面积的散热热阻力为
1
1
=638k/w R,=
h(πd2-12xδ)H 25w/(㎡*k)x(πx0.006-12x0.0007) 肋片根部与肋片的等效热阻力为
R = Σ
R=(24.3-1+638')-'k/w=23.4k/w 딩
于是从晶体管表面到空气的总热阻为R
>R=(13.3+0.054+23.4)k/w=36.8k/w ///
total
晶体管的功耗就是热流量
(80-20)k
=1.63w 「ュー
R1ot
36.8k/w 讨论:(1)肋片的效率
th(mH)
0.204
=O.986 7f
mH
0.207 肋片根部温度为
to=t-ΦΣR=80C-1.63wx(13.3+0.054)k/w=58.2℃ 所以肋片表面的平均温度为
tm=t,+n,(to-t,)=[20+0.986x(58.2-20)}C=(20+37.7)℃=57.7℃C 这一温度明显高于环境温度,因此通过辐射还有一定的散热量。本例中空气为强制对流,表面传热系数较大,略去辐射的影响还可以接受,如何确定辐射散热将在以后考虑
(2)如果晶体管不采用铝制翅片,仍然假定原来的表面传热系数之值,则在80℃的温度限制下,晶体管能达到的功率为
ф=hA,(to-t,)=25w/(㎡*k)x(πd,H+πd?/4)㎡x(80-20)℃ =25w/(㎡*k)x(12.56+1.26)x10-5㎡x60℃=0.21w 可见铝制翅片的作用十分明显。
(3)本例也可以采用肋片总效率来计算
(4)注意下列换算(a)从面积热阻到总热阻的换算;(b)从单个肋片热阻到12个肋片总热阻的换算
专业资料
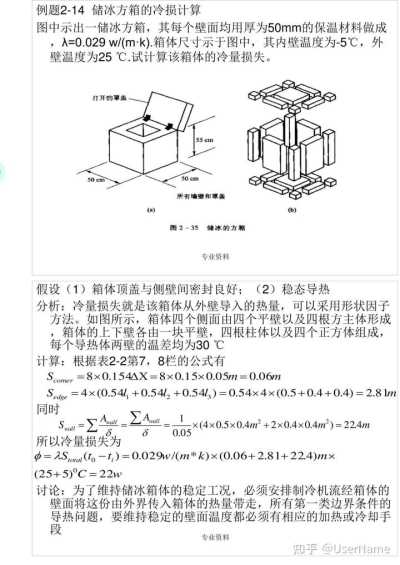
例题2—14 储冰方箱的冷损计算
图中示出一储冰方箱,其每个壁面均用厚为50mm的保温材料做成,λ=0.029w/(m·k).箱体尺寸示于图中,其内壁温度为—5℃,外壁温度为25℃.试计算该箱体的冷量损失。
打开的單盖
55cm 50cm
50cm 所有墙壁和罩盖 (a)
(b) 图2-35
储冰的方箱
专业资料
假设(1)箱体顶盖与侧壁间密封良好;(2)稳态导热
分析:冷量损失就是该箱体从外壁导入的热量,可以采用形状因子方法。如图所示,箱体四个侧面由四个平壁以及四根方主体形成,箱体的上下壁各由一块平壁,四根柱体以及四个正方体组成,每个导热体两壁的温差均为30℃
计算:根据表2—2第7,8栏的公式有Scomer=8x0.154ΔX=8x0.15x0.05m=0.06m
Sedge=4x(0.5411+0.54l2+0.54/3)=0.54x4x(0.5+0.4+0.4)=2.81m 同时
Σ A Σ A 1
x(4x0.5x0.4㎡+2x0.4x0.4㎡)=22.4m wall
wal S
all δ δ
0.05 //
所以冷量损失为
Φ=λStotal(to-t)=0.029w/(m*k)x(0.06+2.81+22.4)mx (25+5)℃=22w
讨论:为了维持储冰箱体的稳定工况,必须安排制冷机流经箱体的壁面将这份由外界传入箱体的热量带走,所有第一类边界条件的导热问题,要维持稳定的壁面温度都必须有相应的加热或冷却手段
专业资料
例题3-1
一直径为5cm的钢球,初始温度为450℃,突然被置于温度为30℃的空气中。设钢球表面与周围环境间的表面传热系数为24W/(㎡.K),试计算钢球冷却到300℃所需的时间。已知钢球的c=0.48kJ/(kg.K),p=7753kg/m3,λ=33W/(m.K)。
题解
假设:(1)钢球冷却过程中与空气及四周冷表面发生对流与辐射换热,随着表面温度的降低辐射换热量减少。这里取一个平均值,表面传热系数按常数处理。(2)常物性。
计算:首先检验可否用集中参数法。为此计算Bi数:
专业资料
hx4/3m/(4mR}) (V/A)
Bi
Y Y
0.025m 24W/(㎡·K)x
3
=0.006 06<0.033 3 33 W/(m·K)
可以采用集中参数法。hA
24 W/(㎡2·K)x4πx(0.025m)2
=7.74x10-48* pcV 7753 kg/m3x480 J/(kg·K)x(0.025m)
据式(3-9)有
专业资料
R}3
1-1,300℃-30℃
=exp(-7.74x10r) 450℃-30℃
1-9 由此解得
t=570s=0.158h
讨论 本例是在已知表面传热系数的条件下计算的,所设定数值的大小对计算结果影响很火。如果为了获得金属球与冷却液体间的表面传热系数,在已知cp和几何尺寸的情况下,你能否设计出一种方法,以通过测定金属球非稳态导热过程中的温度变化而获得所需的表面传热系数h之值。
专业资料
例题3—2 一温度计的水银泡呈圆柱形,长20mm,内径为4mm,初始温度为%,今将其插入到温度较高的储气罐中测量气体温度。设水银泡同气体间的对流传热表面传热系数为11.63 W/(㎡·K),水银泡一层薄玻璃的作用可以忽略不计,试计算此条件下温度计的时间常数,并确定插入5min后温度计读数的过余温度为初始过余温度的百分之几?水银的物性参数如下:c=0.138kJ/(kg·K),p=13 110kg/m,λ=10.36 W/(m·K)。
题解
假设:(1)以计算水银泡部分作为分析对象,略去玻璃柱体部分的影响;(2)常物性。计算:首先检验是否可用集中参数法。考虑到水银泡柱体的上端面不直接受热,故
πR'l
Ri
0.002mx0.02m
=0.953x10^3m A
A 2πRl+mR2 2(l+0.5R) 2x(0.020m+0.001m) Bi=
h(V/A)11.63 W/(㎡·K)x0.953x10-3m
=1.07x10^<0.05 10.36 W/(m·K)
Y
可以采用集中参数法。时间常数为
pcV 13 110kg/mx138J/(kg·K)x0.953x10-m
=1485 hA
11.63 W/(㎡·K) 专业资料
Fo=
鄭
10.36 W/(m·K)
5x60s 13110 kg/m'x138 J/(kg·K)(0.953x10-1m)2 =1.89x10
分
=exp(-Bi·o)=x(-107x10x1.89x10) =exp(-2.02)=0.133
即经5min后温度计读数的过余温度是初始过余温度的13.3%。也就是说,在这段时间内温度计的读数上升了这次测定中温度跃升(从4上升到流体温度1)的86.7%。
例题3—3 一直径为5cm、长30cm的钢圆柱体,初始温度为30℃,将其放入炉温为1200℃的加热炉中加热,升温到800℃方可取出。设钢圆柱体与烟气间的复合换热表面传热系数为140W/(㎡·K),钢的物性参数取与例题3—1一样的值,问需多长时间才能达到要求。题解
假设:(1)表面复合传热系数为常数;(2)常物性。计算:首先检验是否可用集中参数法。为此计算Bi:
h(V/A)_h[(ndl/4)/(ndl+2πd/4)] h dl/4 Bi=
Z/P+1 Y Y
Y
140 W/(㎡·K)x0.50mx0.3m/4
=0.049<0.05 33 W/(m·K)
0.3m+0.025m 可以采用集中参数法。因
h 4(l+d/2)
140 W/(㎡·K)x4x0.325m )
1P pc
7 753 kg/mx480 J/(kg·K)x0.05mx0.03m =0.326x10^28-
θ -1
800℃-1200℃ 0.-
30℃-1200℃
=0.342 、
据式(3-6)有
0.342=exp(-0.326x10-2t) 由此解得r=329s。
阳一
例题3—4 一块厚100mm的钢板放入温度为1000℃的炉中加热,钢板一面受热,另一面可近似地认为是绝热的。钢板初始温度t=20℃。求钢板受热表面的温度达到500℃时所需的时间,并计算此时剖面上的最大温差。取加热过程中的平均表面传热系数h=174 W/(㎡·K),钢板的λ=34.8W/(m·K),a=0.555x10-3㎡/s。已知:Bi=0.1时,μ= 0.311 1 rad;Bi=0.5时,μ1=0.6533 rad;Bi=1.0时,μ=0.860 3 rad。
题解
假设:(1)一维问题;(2)热物性为常数;(3)加热过程表面传热系数为常数。
分析:这一问题相当于厚200mm平板对称受热的情形,故可以应用一维平板的分析解。计算:对于此平板
h8_174W/(㎡·K)x0.1m Bi=
=0.5 34.8W/(m·K) Y
/6=1.0
从图3—8查得,在平板表面上8./0。=0.8。另一方面,根据已知条件,表面上的无量纲过余
温度为
θ.1.-1500℃-1000℃
=0.51 θ0 to-t。
20℃-1000℃ 0.0m0.
θ°θ"θ 故得
θ. 0.
=0.51/0.8=0.637 θ
0000θ
据0./0。及Bi数之值,从图3—7查得Fo=1.2,故得
r=1.2
=1.2x
(0.1m)
=2.16x10^s=0.6h ac{}{8
0.555x10-5m/s 另外,由0m=0.6370。得
=0.63700+t=0.637x(20℃-1000℃)+1000℃=376℃ 故得剖面上的最大温差为
Δmx=500℃-376℃=124℃
例题3—5 有一直径为400mm的钢锭,初温■=20℃,将它置于炉温为900℃的炉中加热,试计算加热到表面温度为750℃时所需的加热时间。假定钢锭可近似地视为无限长的圆柱,并取h=174W/(㎡·K)。钢锭的λ=34.8W/(m·K),a=0.695x10-5m2/s。 题解
假设:(1)一维问题;(2)热物性为常数;(3)加热过程的表面传热系数为常数。计算:Bi=
hR 174 W/(㎡·K)x0.20m
=1.0 34.8 W/(m·K)
/8=1.0
从附录查得,在表面上0./0=0.65。根据已知条件,表面上的无量纲过余温度为
6..-t_750℃-900℃
=0.17 0。-1
20℃-900℃ 故得
0.0=0.17/0.65=0.262
00
据Bi=1.0及0/0g=0.262,由附录查得Fo=0.96,故得
R2
(0.2m) t=0.96-=0.96x
=55258=1.535 h a
0.695x10-5m/s 讨论:如果采用拟合公式来计算,则有
㎡=0.1700+
■=1.285 8 rad
A=1.004 2+0.587 7x[1-exp(-0.403 8x1)]=1.199 4
(M)=0.9967+0.0354x1.2858-0.3259x1.2858+0.0577x1.2858=0.6261
0.0.10
=0.17/0.65=0.262 81
所以Fo=0.898≈0.9。
这一结果与查海斯勒图得到的数值基本一致。钢锭的直径实际上常常可以与其长度比较,因而更合理的计算应把它当作二维物体来处理,3.5节中将讨论这一类问题。
例题3—6 一块大平板型钢铸件在地坑
铸件 中浇铸,浇铸前型砂温度为20℃。设在很短时
间内浇铸完成,并且浇铸后铸件的表面温度一
80mm 直维持在其凝固温度1450℃,试计算离铸件底
面80mm处浇铸后2h的温度(图3—13)。型砂的热扩散率a=0.89x10—㎡/8。
题解
图3-13
例题3-6示意图 假设:(1)将铸件底面以下砂型中的非稳
态导热按第一种边界条件的半无限大物体处理;(2)物性为常数。计算:
80x10m η
=0.5
2/at 20.89x10-6m/8x2x3 600s 由附录查得
erf 0.5=0.5205 所以
t=1,+erf0.5(t-1,)=1450℃+0.5205x(20℃-1450℃)=705.7℃
讨论:物体表面与发生相变的物质紧密接触是形成第一类边界条件的常见例子。本例
中,在铸件内部基本凝固之前,假设铸件表面仍处于相变温度不失为一个可接受的近似处理。例题3—7 地面下的埋管是常见的工程与生活设施。考虑埋管深度的一个重要因素是
在当地的气候条件下,埋管处的温度不会导致管内流体冻结或凝固。以输送工业及民用水的埋管为例,埋管处的温度不能低于0℃。设某地冬天地表面温度为10℃,后突然受冷空气侵袭,地表温度下降到—15℃,并维持45天不变,试确定此种条件下45天后地面下温度为0℃处的位置。
题解
假设:(1)采用第一种边界条件的半无限大非稳态导热模型;(2)物性为常数。计算:土壤的物性取c=1840J/(kg·K),p=2050kg/m3,λ=0.52W/(m·K),于是a
专业资料
=λ/(pc)=0.138x10—6㎡/s。利用式(3—40)可写出
(20/22)20=2/0
即
0℃-(-15℃)
(20/2)m=9'0=
10℃-(-15℃) 由附录查得一
x≈0.6,于是 20/2
x=1.2at=1.2x(0.138x10^㎡2/sx3600sx45x24)12=0.88m
讨论:土壤的热物性参数受许多因素的影响,也与各地的地质条件有关,而本例计算结果的准确性在很大程度上取决于热扩散率之值。例如,a值增加一倍,将使所需最小埋管深度增加41%。因此,与其他传热问题的计算一样,为了获得较准确的结果应尽量选用可靠的物性数据。还应指出,第一类边界条件下半无限大物体非稳态导热只是本问题的一个较粗略的模型,因为地表层的温度并不是均匀的,地表面温度阶跃性的变化也只是一种理想化的处理。考虑这些复杂因素时分析解已无能为力,应求助于数值计算。但作为一种工程估算,本题的结果仍有其参考意义。
例题3—8 有一半无限大的物体,初始温度t。=25℃,后其表面温度突然上升到50℃并保持不变。试计算使表面的扰动传递到x=0.01m,0.1m、1.0m及10m等四个地点,且使该处发生0.1℃温度变化所需要的时间。a=10—5㎡/s。
题解
分析:在2—2节中曾指出,傅里叶导热定律是基于热扰动的传递速度是无限大的假定,而实际物体中热扰动的传递又是以有限速度进行的。这样两个看起来是矛盾的概念在处理一般工程导热问题时又是如何统一的呢?本例就是为回答这样一个问题而专门设计的。
计算:上述四个地点温度升高0.1℃后有
1.-t(x)50℃-25.1℃
=0.996
-t。50℃-25.0℃
利用双精度数据对误差函数作数值积分后得η=2.0352时erfη=0.996 0006。由此得
x
=2.0352 20/2
即
4.070 42a 对四个地点的计算结果如下:
x/m
0.01
0.1
1.0
10 t/s
0.603 6
60.357
6 035.67
603 567
例题3—9 钢锭的尺寸为28,=0.5m,26,=0.7m、28,=1m,钢锭的λ=40.5W/(m·K),a=0.722x103m/8,求钢锭置入炉温为1200℃的加热炉中4h后的最低温度与最高温度。其初温1=20℃,取h=348W/(㎡·K)。
分析:该问题的解可由三块相应的无限大平板的解得出。最低温度发生在钢锭的中心,即三块无限大平板中心截面的交点上,而最高温度则发生在钢锭的顶角上,即三块平板表面的公共点1:
假设:(1)物性为常数;(2)加热过程中表面传热系数为常数。计算:设x.y3分别表示与三个尺度相应的坐标轴方向,则有
专业资料
gy Bi,=
348 W/(㎡·K)x0.25m
=2.15 入
40.5 W/(m·K) 0.722x10-㎡/8x4x3600s 20
Fo,=
(0.25m)2
=1.66 8
Bi,
hô2 348 W/(㎡·K)x0.35m
=3.01 40.5 W/(m·K)
Y
ar 0.722x10-㎡/sx4x3600s
=0.849 Fo,=8
(0.35m)2 Bi=-
h8,348 W/(㎡·K)x0.5m
=4.30 40.5 W/(m·K)
Y Fo,=
at_0.722x10-3㎡/sx4x3600s
=0.416 83
(0.5m)2 对平板1:
0.918 8
-1/2 μ=(0.4022+
2.15
=1.097 9 rad
A=1.0101+0.257 5(1-e-0.4271x2.15)=1.164 8 平板中心处
cos(μ1η)=cos 0°=1 平板表面处
cos(μ1η)=cosμ」=cos 62.91°=0.4555 ()
=1.1648xexp(-1.09792x1.66)=0.157 4
=1.164 8xexp(-1.097 92x1.66)x0.4555=0.071 7 (음)
对平板2:
0.918 8
-1/2 μ1=(0.4022+
3)
=1.188 1 rad
A=1.0101+0.257 5(1-e-2.4271x3.01)=1.196 1 平板中心处
cos(μ,η)=cos0°=1 平板表面处
cos(μ1η)=cos 68.08°=0.373 4 (/),
=1.196 1xexp(-1.188 12x0.849)=0.360 8
=1.196 1xexp(-1.188 12x0.849)x0.373 4=0.134 7 (음)
对平板3:
0.918 8 μ=(0.4022+
4.30
=1.274 2 rad
A=1.0101+0.257 5(1-e-.427x410)=1.226 6 平板中心处
cos(μ1η)=cos 0°=1 平板表面处
cos(μ1η)=cos 73.01°=0.292 3 (/)
=1.226 6xexp(-1.274 22x0.416)=0.6243 =1.226 6xexp(-1.2742'x0.416)x0.2923=0.182 5
(0)
据上述计算可得: 钢锭中心温度
=0.157 4x0.360 8x0.624 3=0.035 45 (a)(음/)(/)=θ/
1=0.035 400。+1,={0.03540x(20℃-1200℃)+1200℃]=1158.3℃ 钢锭的顶角温度
=0.071 6x0.134 4x0.1821=0.001 76 (■/)()(/)=8/
t=0.001 760 +1, ={0.001 76x (20℃-1 200℃)+1 200 ℃] =1197.9℃
讨论:钢锭的中心温度及角顶温度显然是钢锭中的最低与最高温度,钢锭的表面温度介于其间。试利用上面计算中已获得的数值计算此时钢锭三个表面的中心温度。
例题3—10 ——直径为600mm、长1000mm的钢锭,初温为30℃,然后置于1300℃的加热炉中。求置入加热炉内4h后钢锭中心的温度。取表面传热系数的平均值h=232 W/(㎡·K),钢锭的导热系数λ=40.5W/(m·K),热扩散率a=0.625x10—㎡/s。
假设:(1)物性为常数;(2)加热过程中表面传热系数为常数。
计算:
0.=(0),(θ), 先讨论厚28=1000mm的无限大平板:
hδ 232 W/(㎡·K)x0.5m Bi=
=2.86 λ
40.5W/(m·K) aT
0.625x10m/sx4x3 600s Fo=
=0.36 8
(0.5m) 采用拟合公式计算:
0.918 8
-1/2 ■=0.4022+
=1.175 7 rad 2.86
L161=(x A=1.0101+0.257 5(1-e
-1 17572x0.36
=0.724 5 0==1.191 Te
00
对于2R=600mm的无限长圆柱,有:
h8 232 W/(㎡·K)x0.30m Bi
=
=1.72 λ
40.5W/(m·K) at
0.625x10-3m2/sx4x3 6008 Fo=
^{
(0.30m)
=1.0 -1/2
0.0401
=1.537 8 rad ■=0.17+
1.72 A=1.004 2+0.587 7(1-e
-0,4038x1.72
)=1.2985 θm
-1.53782x1.0 =1.298 5e
=0.1220 00
专业资科
短圆柱中心的温度为
=0.724 5x0.122 20=0.0884 16=(f/1(/1)
1n=0.08840+1,=[0.0884x(30℃-1300℃)+1 300℃]=1 187.7℃ 讨论:如果把这一钢锭作为无限长柱体处理,则将得到
1,=0.122 00,+1,=[0.1220x(30℃-1300℃)+1 300℃]=1145.1℃ 这说明短圆柱比无限长圆柱加热得快,试分析其原因。
对于几何形状复杂的物体,或几何形状虽不复杂但边界条件复杂的问题,分析解法已无能为力。在这种情况下,可以采用数值解法或实验模拟法求解。由于近年来计算机应用的迅速发展,数值解法越来越显示出其重要性,下一章将专门予以介绍。
例题3—11 有一直径D=4cm、高H=6cm的牛肉柱体,初始温度为10℃,后置于环境温度为180℃的炉中加热,表面传热系数为15W/(㎡·K)。问需经过多长时间牛肉的温度才至少达到80℃?在这一过程中牛肉吸收的热量是多少?
分析:牛肉的温度至少达到80℃就是柱体的中心温度应该达到这一温度。
假设:(1)牛肉中大部分为水分,近似地用水的物性来估算;(2)牛肉柱体的各个表面同时受到加热;(3)以(10℃+80℃)/2=45℃来确定从开始加热到中心温度为80℃水的物理特性,按(10℃+180℃)/2=95℃来决定计算总加热量的物性。
计算:(1)所需时间计算由附录并插值得
p=990.1 kg/m,c,=4.174 kJ/(kg·K),λ=64.2x10-2W/(m·K), a=15.5x10-㎡/s
本题采用Campo的拟合公式方法。(a)构成短圆柱的一—维平板计算Bi=
h8_15W/(㎡·K)x0.03m
=0.702 λ
64.2 W/(m·K)
人
0.918 8 ㎡=(0.4022+
0.702
=0.584 1
A=1.010 1+0.257 5(1-exp( -0.427 1x0.702)=1.076 8 B=
1.006 3+0.348 3x0.702
=0.903 6 1+0.547 5x0.702
8(0,7)
=1.076 8exp(-0.5841xp0) 00
=1.0768emp(-0.58418o。)x0.9036=0.9730xexp(-0.584180) 00
(b)构成短圆柱的一维圆柱
hR 15W/(㎡·K)x0.02m Bi=
=0.467 6 64.2W/(m·K)
Y
0.4349 A=0.1700+
0.4676
=0.9091
A=1.004 2+0.587 7x[1-exp(-0.403 8x0.467 6)]=1.105 3 1.0173+0.257 4x0.467 6
B
=0.888 9 1+0.598 3x0.467 6
(10)0
=1.105 3exp(-0.909|Fo。)x0.996 7=1.101 7exp(-0.909 1Fo,) °
0=1.105 3exp(-0.909 1Fo,)x0.889 9=0.983 6exp(-0.584 1Fop) °
故短圆柱的无量纲中心温度为
=1.076 8exp(-0.584 1Fop)x1.101 7exp(-0.909 1Fo) (음) (음)=9/
at
15.5x10㎡/sx7
=1.7222x10-15x Fop=8
(0.03m)2 Fo
15.5x10(㎡/s)r
=3.8750x1045-1xt αt
R2
(0.02m)2 代入并合并同类项得:
6.
=1.186 3exp(-4.5289x104sxr)
10 θ。
17 由此解得T=1549s。
验算:此时
Fo,=1.7222x10^4x1549=0.2667>0.2
Fo。=3.8750x10-4x1549=0.6002>0.2 (2)牛肉吸收热量的计算
牛肉柱体的体积为
V=0.785D2H=0.785x(0.04m)2x0.06m=7.536x10^3m 将已经求出的所需时间代人,得
=0.9730xexp(-0.584 1x0.2667)=0.832 6 (음)
=0.9836xexp(-0.584 1x0.6002)=0.5693 (음)
故有
(음),=1-/0
=1-0.8326=0.1674 =1-0.5693=0.430 7 ■-1=(응)
=0.167 4+0.4307x(1-0.1674)=0.5260 [(응)-1(응)+(응)=%
Q。=pcV(t■-t)=961.9kg/mx4.21 kJ/(kg-K)x7.536x10-3㎡x(180-10)℃ =51.9kJ
Q=0.5260x51.9kJ=27.3kJ 例题3-12
·在脉管制冷机,斯特林制冷机等工程技术
中,工作介质速度的方向发生交替
变化,流体温度发生周期性脉动,这种流动称为交变流动(oscillating low)。假定在以空气为介质的交变流动中,空气在一个周期内的平均温度为303K,脉动的频率为5Hz,现用钢—康铜热电偶来测定气流的温度随时间的变化。气体流速为20m/s,热电偶热结点直径d=0.9mm,热结点的物理性质为p=8332kg/m,,=188J/(kg·K)、λ=51W/(m·K)。试问这样的热电偶是否能达到要求?
专业资料
题解
分析:要测定脉动频率为5Hz(脉动周期为0.2s)的气流温度,则热电偶本身的时间常数必须远小于0.2s方可测得较准确的数值。因此,本题的计算目的是要确定所给定条件下热电偶的时间常数。
假定:(1)热结点是一个孤立的球体,不考虑与热结点相连接导线的影响;(2)热结点与空气间的表面传热系数可以用流体与球体间的对流传热计算式来确定(这里应用第6章中的公式);(3)不计热结点与周围环境间的辐射传热。
计算:303K空气的热物性为v=16.0x10-6㎡/s、λ=2.67x10^2W/(m·K)、Pr= 0.701(普朗特数,反映流体热物性的影响)。来流的Re数
u.d_20m/sx9x10m=1125 Re=
v
16.0x10㎡/s 小球的平均表面传热系数可按下式计算:
h=2+(0.4Re2+0.06Re232 λ1
=2+(0.4x11252+0.06x11252^3)x0.7012/5 =2+17.2=19.3
19.3x26.7x10-2W/(m·K)
=591 W/(㎡·K) 9x10m
hd_591 W/(m·K)x9x104m Bi=
=0.01 51 W/(m·K)
Y
满足采用集中参数法的条件。所以
pcV_8332 kg/m'x188J/(kg·Kx4.5x10*m) Te=
=1.198 Ah
591 W/(㎡·K)x3
讨论:此值大于温度的脉动周期,因此该直径的热电偶无法测定这一交变流动的温度随时间的变化。需要将直径减小到多大才能满足要求留给读者在习题中去完成。
专业资料
例题3—13 电熨斗烫衣料。
用电熨斗来烫平一块厚的衣料。熨斗表面的热流密度g0=2x10^W/㎡,衣料的初始温度为20℃,热扩散率a=10㎡/s,导热系数λ=0.2W/(m·K)该衣料的烫焦温度为180℃。如果熨斗连续在衣料表面上同一地点放置306,问衣料表面以及其下3mm处的温度是多少?
分析:此题可以采用第二类边界条件的半无限大物体的简化模型来分析。
假设:(1)熨斗放在衣料上后该处仍然保持原有的形状;(2)熨斗的热量全部传到衣料中;(3)常物性。
计算:计算30s后衣料表面及其下3mm处的温度
专业资料 20
240
2x2x10W/㎡x(10-7㎡/sx30s/3.14)2 t(0,r)=t0+-
=20℃
=215.5℃ 0.2W/(m·K)
对x=3mm、t=30s,有
x
(3x10-3m)2
-=0.75 4at 4x10m/sx30s 290aπ
(20/2)00 /0-(20/)d t(x,r)=t0+
=20℃+t(0,x)=10+
=20℃+ Y
2x2x10+W/㎡x(10-1㎡/sx30/3.14)
0.2 W/(m·K)
xexp(-0.75)- 2x10*W/㎡x3x10^m
3x10m x erfc
0.2W/(m·K)
2
10m/6x30s x
=20℃+92.3℃-64.5℃=47.9℃
讨论:30s后衣料的表面温度已经超过烫焦的极限,但是3mm以下处则不到50℃,这是因为衣料的热扩散率极低之故。
专业资科
例题3—14 蔬菜罐头的蒸汽加热消毒。
一直径为10cm、高8cm的蔬菜罐头,初始温度为40℃,被置于饱和温度为105℃的蒸汽中通过蒸汽凝结加热。问80min后罐头中的最低温度及其所吸收的热量。
题解
分析:蒸汽凝结对流传热表面传热系数相当大,可以认为表面热阻为零,即Bi→■;罐头中的最低温度发生在罐头的中心。
假设:(1)罐头四周均匀受热;(2)蔬菜的物性取为水的值;(3)罐头内为纯导热作用,没有对流;(4)不计罐头金属包壳的影响。
计算:以(40+80)℃/2=60℃计算物性有
p=983.2kg/m3,c,=4 179 J/(kg·K),λ=65.9x10-2W/(m·K),a=16x10-*m/s 对于8cm厚的平板
at
16.0x10-㎡/sx4800s Fo=
=0.48 (0.04m)
对于10cm直径的圆柱
ar
16.0x10→5㎡/sx4800s Fo=
=0.307 R
(0.05m) 可以采用正规状况阶段的简化解,采用拟合公式法。对平板
㎡=(a+/)
=0.4022-1=2.486 3
A=a+b[1-exp(-cBi)]=0.4022+0.918 8=1.321 0 B=
a+cBi c_0.348 3
=0.6362 1+bBi b 0.547 5
J。(η)=a+bn+c㎡2+dn=a=0.9967
()=exp(-)(0)=1.321xcxp(-2.4863x0.48)x1.0000=0.400 (/)=Aexp(-μ}Fo)B=1.321xexp(-2.4863x0.48)x0.636 2=0.255 (음), =1-(:).
=1-0.255=0.745 对于一维圆柱
=0.1700=5.8824 (/+0)=
A=a+b[1-exp(-cBi)]=1.0042+0.5877=1.591 9 a+cBi
0.257 4 =8
J+bBi b 0.5983
=0.4302 Jo(η)=a+bη+c㎡+dn'=a=0.9967
=Aexp(-㎡Fo)f(0)=1.5919xexp(-5.8824x0.307)x0.9967=0.261 (음)
(음).
=Aexp(-μFo)B=1.5919xexp(~5.882 4x0.307)x0.4302=0.113
(음),=1-(/).
=1-0.113=0.887
蔬菜罐头
=0.400x0.261=0.104 4 (응)(음/)=4/
--105℃ ■-140℃-105℃
=0.104 4.1=98.1℃
=0.745+0.887x(1-0.745)=0.971 2 [(음)-(음)+(/)=0/0
仍然以60℃的物性值计算Q0,则有
Q=0.971 2x983.2 kg/m'x4 179 J/(kg·K)x3.14x(0.05m)2x0.08mx(105-40)K =162.9kJ
讨论:分析解是对常物性问题作出的,实际物体的物理性质多少与温度有关。但只要物性数值变化不是太大,取某个平均温度[这样的温度称为定性温度(reference temperature)]下的物性进行计算一般足够准确 上例中,如果计算(。的温度取为70℃,p=977.7 kg/m',c,=4 187 J/(kg·K),则所得之值相差仅0.4%,完全在工程计算允许的误差范围内。
例题4—1用高斯—赛德尔迭代法求解下列方程组8t1+2t2+t3=29 11+5t2+2t3=32
21++4t3=28 解题:分析先将上式改写为以下迭代形式
(29-2t2-t3) (32-11-2t3)
(28-21,-t2)
注意对上述改写后的方程组,迭代收敛的条件是满足的,假设一组初值,例如取)
=t (0) =t (0) =0
利用上述迭代方程式可以得出第一次迭代的结(0)
x
果。经过数次迭代后就可获得所需的解。
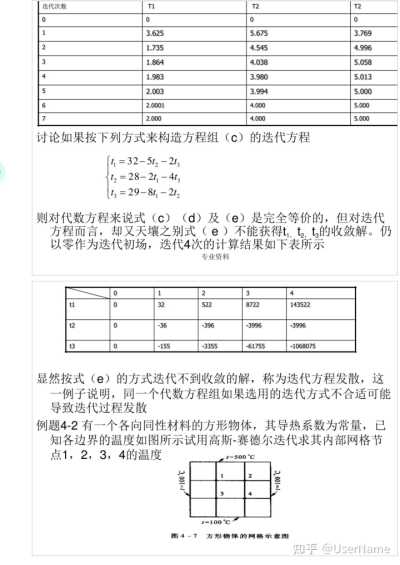
计算:经过7次迭代后,在四位有效数字内得到了与精确解一致的结果,迭代过程的中间值如下
专业资料 ac{1}{81l5rac{1}{4}
迭代次数
T1
T2
T2 0
0
0
0 1
3.625
5.675
3.769 2
1.735
4.545
4.996 3
1.864
4.038
5.058 4
1.983
3.980
5.013 5
2.003
3.994
5.000 6
2.0001
4.000
5.000 7
2.000
4.000
5.000 讨论如果按下列方式来构造方程组(c)的迭代方程
■=32-5t2-2t3 {t2=28-2t-4t3
t3=29-8t1-2t2
则对代数方程来说式(c)(d)及(e)是完全等价的,但对迭代方程而言,却又天壤之别式(e)不能获得t,t2.t的收敛解。仍以零作为迭代初场,迭代4次的计算结果如下表所示
专业资料 0
1 2 3
4 t1
0
32 522 8722
143522 0
t2
-36 -396 -3996
-3996 t3
-155 -3355 -61755
-1068075 0
显然按式(e)的方式迭代不到收敛的解,称为迭代方程发散,这一例子说明,同一个代数方程组如果选用的迭代方式不合适可能导致迭代过程发散
例题4—2有一个各向同性材料的方形物体,其导热系数为常量,已知各边界的温度如图所示试用高斯—赛德尔迭代求其内部网格节点1,2,3,4的温度
=500℃ 1 2 3
4
r-100℃
图4—7 方形物体的网格示意图
200le)
t=100℃
题解
分析,这是一个三维稳态导热问题,对于物体内部每个网格节点的温度式(4—2)的关系适用。从形式上看式(4—2)中主对角元t的系数正好等于四个相邻节点的系数之和,但注意到,对所计算的问题每个节点都有两个邻点是边界节点,其温度值是已知的。在写成代数方程的通用形式时,温度知已知的项应该归于常数项b中,故主对角元的系数大于邻点系数之和的要求仍然满足,迭代法可以获得收敛的结果。
计算;假设t(0)
=t2 (0)
=300C,t3
(0) (0) =200C 1一
4 应用式(4—2)按高斯—赛德尔迭代得
专业资料 1
(500C+100C+t+30) -x
4
1x(500+300+100+200)℃=275C 4
(1) 1
(500°C+100C+t,(1)+t(0) 十
4 1
x(500+275+100+200)℃=268.75℃ 4
1
x(100°C+100℃+1(1+0) {3}
4
1x(100+275+100+200)℃=275℃ 4
1 t(1)
(500C+100°C+t+() x
4 1
(100+268.75+100+168.75)℃=159.38℃ x
4
依次类推,可得其他各次迭代值。第1到5次迭代值于下表,其中第5次与第6次迭代的相对偏差按或4—10b已小于2x104迭代终止
迭代次数
t1/℃
t2/℃
t3/℃
t4/℃
0
300
300
200
200
1
275
268.75
168.75
159.38
2
259.38
254.69
154.69
152.35
3
252.35
251.18
151.18
150.59
4
250.59
250.3
150.03
150.15
5
250.15
250.07
150.07
150.04
6
250.04
250.02
150.02
150.01
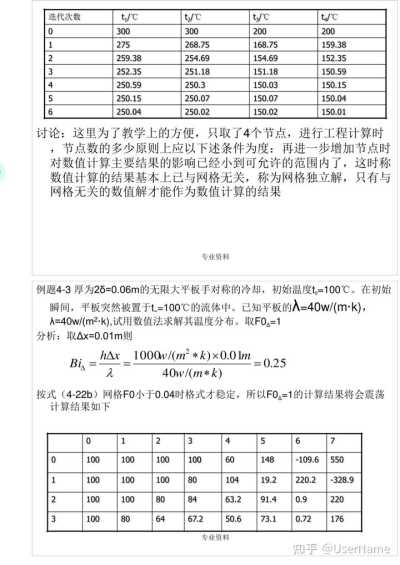
讨论:这里为了教学上的方便,只取了4个节点,进行工程计算时
,节点数的多少原则上应以下述条件为度:再进一步增加节点时
对数值计算主要结果的影响已经小到可允许的范围内了,这时称
数值计算的结果基本上已与网格无关,称为网格独立解,只有与
网格无关的数值解才能作为数值计算的结果
专业资料
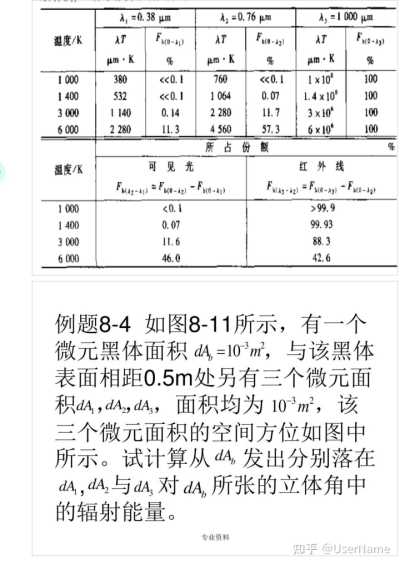
例题4—3厚为25=0.06m的无限大平板手对称的冷却,初始温度t。=100℃。在初始
瞬间,平板突然被置于t=100℃的流体中。已知平板的λ=40w/(m·k),
λ=40w/(m2·k),试用数值法求解其温度分布。取FOA=1
分析:取Δx=0.01m则
hΔx
1000v/(㎡*k)x0.01m
Bi=
40w/(m*k)
=0.25
λ
按式(4—22b)网格F0小于0.04时格式才稳定,所以FOA=1的计算结果将会震荡
计算结果如下
0
1
2
3
4
5
6
7
0
100
100
100
100
60
148
-109.6
550
1
100
100
100
80
104
19.2
220.2
-328.9
2
100
100
80
84
63.2
91.4
0.9
220
3
100
80
64
67.2
50.6
73.1
0.72
176
专业资料
例题8-3
试分别计算温度为1000K,1400K,3000K,6000K时可见光和红外线辐射在黑体总辐射中所占的份额。
题解
分析:可见光和红外线的波长范围分别为0.38~0.76μm和0.76~1000μm。将给定温度各自乘以0.38μm,0.76μm,1000μm,从而得到各个xT值,然后根据这些aT值,在表8—1上查得各自的能量份额Fb(0—2)
值, 再据式(8—11)计算出可见光和红外线辐射各自占的份额。
计算:按上述方法计算得到的结果列出于下表中。
讨论:可见,在T<1000K时黑体辐射中可见光所见的比例远不到1/1000,只有温度上升到3000K左右时可见光的比例才可达10%以上。这一关于可见光在物体自身辐射中所占的比例,总体上对大多数实际物体的辐
专业资料
射也适用。
λ1=0.38
λ2=0.76 μm
λ3
=1000 μm
μm FB(0-A2)
λT
Fb(0-k3) 温度/K
λT
λT (1-0)9g
μm·K
μm·K
% μm·K
%
% <<0.1
760
<<0.1 1x10
100 1 000
380
1.4x10°
100 <<0.1
1064
0.07 1400
532
3x10°
100 3 000
1 140 0.14 2 280
11.7 11.3
4 560 57.3
6x106
001 2 280
% 000 9
所占
份额 可见光
红外线 温度/K
=F
-Fb(0-A2) F
b(λg-x2)
5(0-A3) Fb(x2-■1)
=Fu(0-k2) -F6(0-N1)
>99.9 1 000
<0.1
99.93 1 400
0.07
88.3 3000
11.6
42.6 6 000
46.0
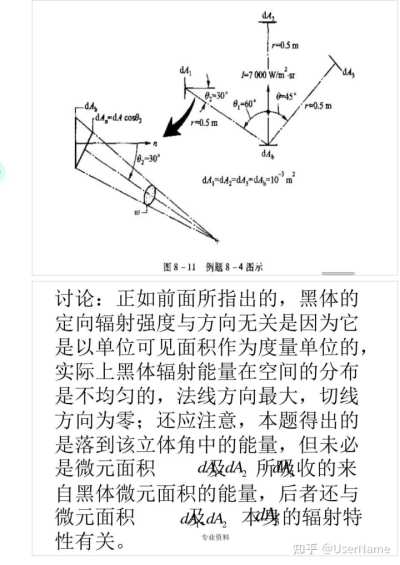
例题8—4 如图8—11所示,有一个微元黑体面积d=103㎡,与该黑体表面相距0.5m处另有三个微元面积dA,dA2,dA3,面积均为10—3㎡,该三个微元面积的空间方位如图中所示。试计算从dA,发出分别落在dA,,dA2与dA3对dA,所张的立体角中的辐射能量。
专业资料
题解
分析:先根据dA,dA2与dA3的大小与方向确定它们对dA,所张的立体角,然后根据式(8—15a)即可得出所求解的能量。
计算:据式(8—12)有:
dA
10-3㎡ cos 30 dΩ
=3.46x10-3sr (0.5m)2
dA
10-3㎡cos0° dΩ22
=4.00x10-3sr (0.5m)
dA
10-3㎡cos0
3 dΩ3
4.00x10
sr 专业资料
(0.5m)
dΦ(60)=1dA,cosθ,dΩ2=7000W/(㎡2.sr)x(10^-3㎡2)
-x3.46x10-3sr =1.21x10-2W
2
dΦ(0)=ldA,cosθ2dΩ22=7000W/(㎡·sr)x(10-3㎡2)x4.00x103sr =2.80x10-2W
dΦ(45)=1d4,coso,dΩ2=7000W/(㎡2.sr)x(10㎡)
rac{2}{
x4.00x10-3sr C
=1.98x10-2W
专业资料
1 } }
r=0.5m
1 dA
1=7000 W/m-sr
dA3 θ2=30°
0-45°
r=0.5m dA=dA cosθ2
r=0.5m dAp -3 2
dA,=dA2=d43=dA=10m 图8—11 例题8—4图示
讨论:正如前面所指出的,黑体的定向辐射强度与方向无关是因为它是以单位可见面积作为度量单位的,实际上黑体辐射能量在空间的分布是不均匀的,法线方向最大,切线方向为零;还应注意,本题得出的是落到该立体角中的能量,但未必是微元面积
d及dA2所吸收的来自黑体微元面积的能量,后者还与微元面积
d及dA2本身的辐射特专业资料
性有关。
例题8—5 试计算温度处于1400℃C的碳化硅涂料表面的辐射力。
题解
分析:碳化硅涂料是非导体,可取ε=8n。
计算:由表8—2查得,碳化硅涂料在1400℃C时的εn=0.92,亦即ε=0.92。按照式(8—18),其辐射力为
(14070+273)x E=εC
100
=409x103W/㎡=409kW/㎡
讨论:一般工业手册中给出的发射率常为法向发射率,选用时应注意表面类型与状态而作相应修正。对于本例,要注意给定的温度范围是与发射率范围相对应的。
专业资料
·例题8-6
.
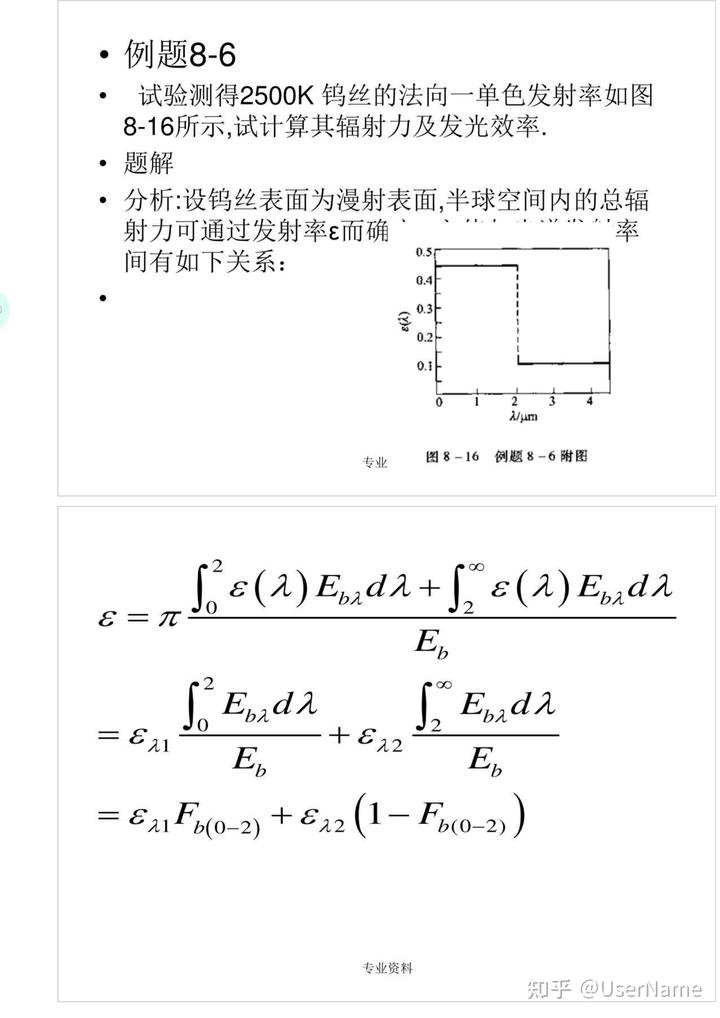
试验测得2500K钨丝的法向一单色发射率如图8—16所示,试计算其辐射力及发光效率.
·题解
·分析:设钨丝表面为漫射表面,半球空间内的总辐射力可通过发射率ε而确
率 间有如下关系:
0.4 0.3 40 0.2 0.1 0 1 2
λ/μm 专业
图8—16 例题8—6附图8
(x)Eb2dλ+2
ε(x)Ebadλ 1=3
Eb 2
8 Ebdλ
Ebadλ 07
2
3+ 3=
λ1
λ2 Eb
Eb F
十 b(0-2)
(1-Fb(0-2)) 3=
3 λ1
λ2
专业资料
计算:AT=2x10-6μmx2500K=5000μm·K, =0.6341
Fb(0-2)
ε=0.45x0.6341+0.1x(1-0.6341)=0.322
2500
K E=8P,=0.332x5.67W/(㎡·k1)x
100 =7.13x105W/㎡
专业资料
取可见光的波长范围为0.38~0.76μm,则λT=950μm·K,1T=1900μm·K。由表8—1,近似地取F
=0.0003, b(0-0.38)
Fb(0-0.76)
=0.0521。于是,在可见光范围内发出的能量ΔE为
2500
K ΔE=(0.0521-0.0003)x0.45x5.67W/(㎡.K)x(
100 =5.16x104W/㎡
ΔE_5.16x104W/㎡ 发光效率为η=
=0.0727=7.27% E
7.16x105W/㎡ 专业资料
·讨论:自从爱迪生发明第一只白炽灯以来,
已经历了百余年。白炽灯由于灯丝的工作温度相对较低,热辐射中可见光的比例甚少,因此发光效率不高。大部分能量都作为不可见的红外辐射的能量而没有予以利用。发展新的固态光源(如发光二极管,LED)作为白炽灯,荧光灯以后的第三代照明技术是节约能源的重要措施,已经引起世界各国的重视。
专业资料 例题8-7
一火床炉的炉墙内表面温度为500K,其光谱发射率可近似地表示为:
λ≤1.5μm时ε(x)=0.1;λ=1.5~10μm时ε(λ)=0.5; x
10μm时ε(x)=0.8。炉墙内壁接受来自燃烧着的煤层的辐射,煤层温度为2000K。设煤层的辐射可以作为黑体辐射,炉墙为漫射表面,试计算其发射率及对煤层辐射的吸收比。
题解
分析:炉墙的发射率可以按定义由以下分段积分来获得:
专业资料
21
λ2 E
dλ
E dλ
J2
dλ 吖
29日 bλ
bλ 3=3
+8x3
Eb +8x2
Eb 12
Eb 上 b(0-21)
F b(x1-x2) + 8x3 b(x2-00)
x 3=
3+ 21
λ2
按定义,炉墙的吸收率为:a(x,T,)E2(T2)d =0
{2} E
b2(I2)dλ
由于炉墙为漫射体,所以有ε(λ,T)=α(λ,T),
由此可得: b(0-21)
A b(11-λ2)
23 F
b(x2-00) A
λ2 3=0
21
十 3
+ 3
专业资料
·计算:对于炉墙的发射率,有:AT=1.5μmx500K=750μm·K,F
=0.000
b(0-11) ■T1=10μmx500K=5000μm·K,F
=0.634
b(0-x2) 所以:
ε(TG)=0.1x0.000+0.5x0.634+0.8x(1-0.634)=0.61
炉墙吸收的是2000K时的辐射,应按2000K计算λT,即:
专业资料
AT2=1.5μmx2000K=3000μm·K,F
b(0-21)
=0.274 AT2=10μmx2000K=20000μm·K,F
=0.986
b(0-x2)
a(T,T2)=0.1x0.274+0.5x(0.986-0.274)+0.8x(1-0.986)=0.395 讨论:由计算得ε(T,)=0.61,而α(T,T2)=0.395,α≠8。
这主要是由于在所研究的波长范围内,α(λ)不时常数所致。
专业资料
·例题8-8
·人造卫星表面对太阳辐射吸收率的允许值的估计。
R=1m
ε=0.75
G3 图8—27 例题8—8图示
专业资料
·如图8—27所示,一个研究卫星绕地球的近极点的轨道运行,使得卫星可以总是受到太阳的直接辐射。为了姿态控制,卫星绕与轨道相一致的轴旋转。卫星呈球形,外径1m,其内的各种电子器件的散热量为1250W。卫星的外壳需要维持在265~305的温度。已知壳体的发射率为0.75,其温度均匀。试估算能允许的卫星表面对太阳能辐射的吸收率。
专业资料
·题解
·分析:卫星与太阳间的辐射作用是卫星最主要的传热过程,因此可假设不考虑卫星与地球间的辐射换热,宇宙空间按0K的物体处理,则卫星表面得到的是太阳的辐射和内部电子器件的散热量,传递到宇宙空间的是其自身辐射,根据热平衡有:
专业资料
a,G,A+фc=εσT4A
其中α,是卫星表面的吸收率,A为卫星接收太阳辐射的面积,ø是电子器件的功率。于是有
4πR2εσT4-φ α
πR2G
计算:卫星需要维持外表面温度在265K到305K之间。因此最小与最大的吸收率分别为:
4πx1㎡x0.75x5.67x10-8W/(㎡.k4)x(265K)4-1250W αs,min
πl㎡x1367W/㎡ =0.323
4πx1㎡x0.75x5.67x10-8W/(㎡2·k+)x(305K)4-1250W αs,max
πl㎡x1367W/㎡ =0.786
专业资料
·讨论:为使卫星表面对太阳辐射的吸收率达到所需的值,可对表面材料敷设专门的涂层。在太空飞行的物体,辐射是其散热的唯一方式,所以航天事业是促进辐射传热研究发展的主要动力之一。本章宜用的辐射名著的作者就是长期从事美国航天事业的研究者。
专业资料
·例题8-9
·测定吸收比与发射率的实验。
·图8—28给出了一种测定表面发射率与吸收比的装置示意图。一直径为30mm的圆柱形试样受水冷却,被置于一个大的腔体的右上角。壳体内壁面为漫灰体,发射率为0.8。该试样的光谱反射率如上图所示。试验中测得稳定工况下试样表面温度为
T,=300K,腔体内表面温度为T,=1000K,其中充满1000K的空气。冷却水带走的热量为24.4W。试计算该条件下试样的吸收比与发射率,以及试样表面与空气间的对流传热系数。试样是不透明的漫射体。
专业资料
一试样
1 0.8 0.2 0 0
246 8
01
2/μm
图8—28 一种测定表面发射率,吸收比的装置示意图
专业资料
·题解
·分析:热平衡时,试样从大腔体得到的辐射能,从空气对流得到的能量,减去其自身辐射应等于被冷却水带走的热量。故有:
Φcool=A[αG(T)+Φcomv-εE,(T,)]= A[αG(T)+h
conv
(T,-T)-εE,(T)] 为了计算h
需要先求出发射率和吸收比。C
腔体的体积很大,它对试样的投入辐射就是1000K下的黑体辐射。因为试样不透明,所以光谱吸收率α(λ)=1—p(λ)。据此可按定义计算试样的吸收率等。
专业资料
·计算:试样的吸收率为
α=a()Gdλ/G=1-)(1000K)dλ/(1000K)
十
b(0-4)
+ α=(1-p(x))Fb(0-3)
(1-p(3))Fb(q-x2)=(1-p(3))F (1-p(1))(1-F)(0,-x1)
据表8-1,AT=4x1000μm·K=4000μm·K,Fb(0-4)
=0.4813。 故有:α=(1—0.2)x0.4813+(1—0.8)x(1—0.4813)=0.481
按发射率的定义。有 E(T)
I(x)Em2(300K)dλ/E,(300K)= E,(T)
(1-p(x))F
十
-(1-p(22))(1-FD(0-x1) b(0-■)
专业资料
据表8-1,AT,=4x300μm·K=1200μm·K,F
=0.002
b(0-21) ε=(1-0.2)x0.002+(1-0.8)x(1-0.002)=0.2
根据发射率和吸收比之值可以得出对流传热的表面传热系数之值为:
1
Pa-aG(T,)+eE,(T) hcom
T,-T,
24.4W 1
3.14/4x0.03㎡
0.481x5.67x108W/(㎡2·K4)x(1000K)++ (1000-300)K
0.2x5.67x108W/(㎡2·K4)x(300K) =10W/(㎡·K)
专业资料
讨论:读者也许要问:那么p(λ)又是怎样测定的呢?如图8—28所示,如果在大腔体的底面中间开一个极小的孔,可以分别测出从腔体左右两个顶面上发出的总的辐射能。由于试样本身温度较低,可以认为试样向外发射的主要是反射的能量,对波长λ,反射能量正比于p(x)G2,从图中的A方向用测定定向辐射强度的仪器可以测定这份能量,而从B方向则可测定正比于E2(T1)的能量,因为G1(T)=Eba(I,),所以两者之比既为p(x)。
专业资料
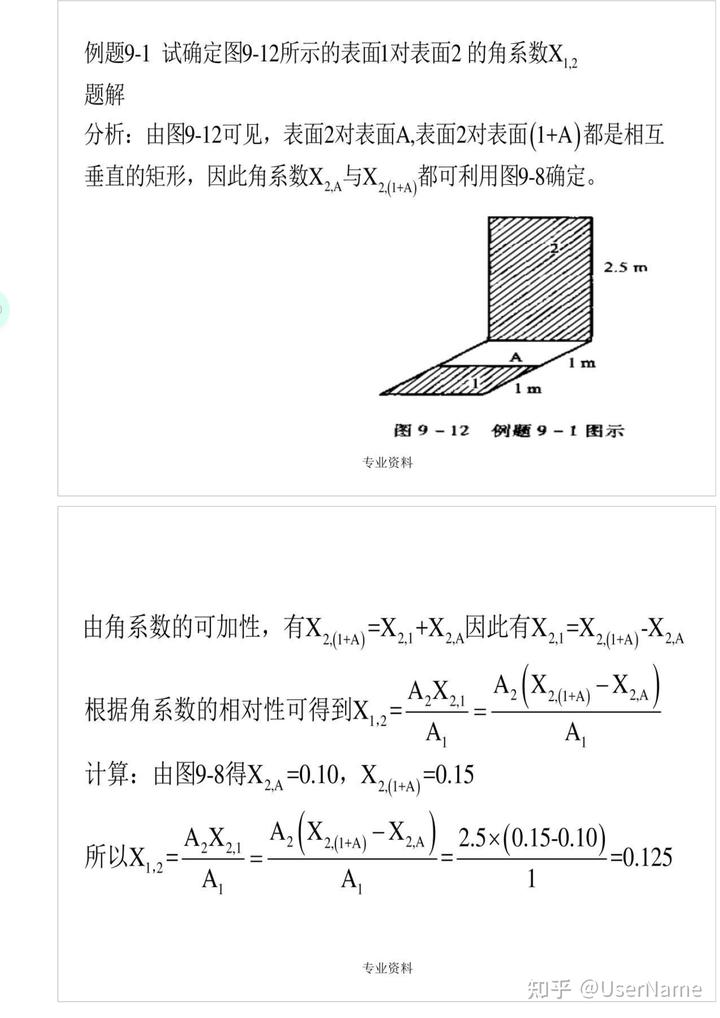
例题9—1 试确定图9—12所示的表面1对表面2的角系数X
1,2 题解
分析:由图9—12可见,表面2对表面A,表面2对表面
(1+A)
都是相互 垂直的矩形,因此角系数X,与X
都可利用图9—8确定。2.A
2,(1+A)
2.5m A
1 m
1m
图9—12 例题9—1图示专业资料
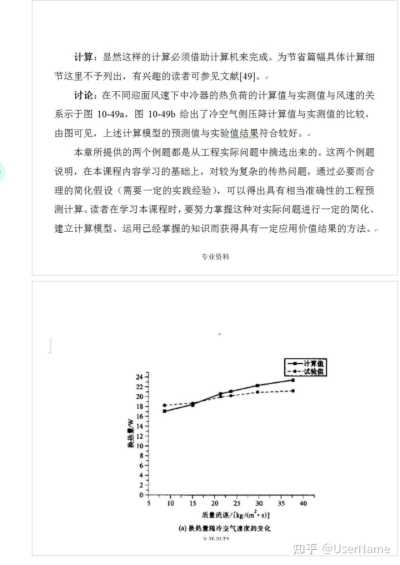
由角系数的可加性,有X
2,(1+A) =X
因此有X
=X 2,(1+A)
-X X+
2,1 2,A
2,1
2,A +
A2X
A2(X
2,(1+A) 根据角系数的相对性可得到X
2,1
2,A 1,2
A1
A1 计算:由图9—8得X,A=
=0.10,X
=0.15 2,A
2,(1+A)
X- A2X
A2(X 2,(1+A)
2.5x(0.15-0.10) 所以X
2,1
2,A
=0.125 1,2
A1
A1
1 专业资料
讨论:利用这样的分析方法可以得出不少几何结构
的角系数,习题中将有更多这样的例子。采用代数分析法时最终得到的答案往往是一个比较小的数。因而计算时要注意有效数字的位数问题。
专业资料
例题9—2液氧储存容器为双壁镀银的夹层结构(图9—17),外壁内表面温度tM=20℃,内壁外表面温度tw2=—183℃,镀银壁的发射率ε=0.02。试计算由于辐射传热每单位面积容器壁的散热量。
图9—16 平行平板间辐射
图9—17 液氧储存容器示意图传热的示意图
专业资料
题解
分析:因为容器夹层的间隙很小,可认为属于无限大平行表面间的辐射传热问题。容器壁单位面积的辐射散热量可用式(9—16)计算。计算T1=tw1+273K=(20+273)K=293K
Tw2=tw2+273K=(-183+273)K=90K co(F)(T)
5.67W/(㎡2·k+)x[(2.93k)'-(0.9k)*] q1.2
=4.18W/㎡ 1
1
1
1 -1
-1 +
+
0.02 0.02 3 3
专业资料
讨论:采用镀银壁对降低辐射散热量作用极大。作为比较,设ε1=82=0.8,则将有q12=276W/㎡,即散热量增加66倍。
如果不采用抽真空的夹层,而是采用在容器外敷设保温材料的方法来绝热,取保温材料的导热系数为0.05W/(mn·k)
(这已经是相当好的保温材料了),则按一维平板导热问题来估算,所需的保温材料壁厚δ应满足下式:
[20-(-183)]K 4.18W/㎡=0.05W/(m·k)x
δ δ=2.43m
因此可见抽真空的低发射率夹层保温的有效性。
专业资料
例题9—3 一根直径d=50mm、长度1=8m的钢管,被置于横断面为0.2mx0.2m的砖槽道内。若钢管温度和发射率分别为t,=250℃,ε1=0.79,砖槽壁面温度和发射率分别为t2=27℃C,ε2=0.93,试计算该钢管的辐射热损失。
题解
分析:这是一个三维问题,但是因为l/d>>1,可以近似地按二维问题处理,而直接应用是(9—15)计算钢管的辐射散热损失。
计算:
AC()(F)
3.14x0.05mx8mx5.67W/(㎡·k)x[(5.23k)*-(3.00k)+
1
3.14x0.05
1
x 1/4(1/-
0.79 4x0.2
0.93 =3.710KW
专业资料
讨论:这一问题也可以近似地采用A,/A2≈0的模型。此时有φ=C,AC(π)-()
=0.79x3.14x0.05mx8mx5.67W/(㎡.k4) x[(5.23k)+-(3.00k)+]=3.754KW
与上述结果只相差1%.
例题9—4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热方法加热,如图9—18所示。在操作过程中需要将炉子顶盖移去一段时间,设此时筒身温度为500K,筒底为650K。环境温度为300K。试计算顶盖移去期间单位时间内的热损失。设筒身及底面均可作为黑体。
专业资料
题解
分析:从加热炉的侧壁与底面通过顶开口散失到厂房中的辐射热量几乎全部被厂房中的物体吸收,返回到加热炉内的比例几乎为零,因此可以把顶盖开口处当作一个
3
T■=300 K
500K
650K 图9-18
例题9-4
的图示 专业资料
假想的黑体表面,其温度则等于环境温度,这样就形成了由3个等温表面组成的黑体封闭腔。加热炉散失到厂房中的辐射能即为ф=23+ф,3=A2X23(Eb2—Eb3)+
A,X13(Eb1-Eb3)
计算:据角系数图9—9,r2/1=0.375/1.5=0.25,1/r,=1.5/0.375=4,得X13=0.06,X12=1-0.06=0.94
3.14x0.752/4 公
据相对性得X
X
x0.94=0.118 2,1
1,2 A
3.14x0.75x1.5 c
专业资料
1=1.5m
再据相对性得X
=X
,故最后得 2,1
2,3
Φ=3.14x0.75mx1.5mx0.118x5.67W/(㎡·K+)x[(5K)-(3K)]+ 3.14
(0.75m)2x0.06x5.67W/(㎡2·K4)x 4
(6.5K)#-(3K)+]=1286W+256W=1542W
讨论:在上述计算中利用9.1节中的式(c)计算两个黑体表面间的辐射传热,该两个表面并未形成封闭系统。这里要特别指出,
专业资料
只有对于黑体表面,不形成封闭腔的两表面之间的辐射传热计算才具有确定的结果;而对于灰体表面,这样的计算不能得出确定的结果,其数值将随环境条件的不同而改变。鉴于这一原因,
本书不讨论不构成封闭腔的任意两表面间的辐射传热,而把注意力集中到工程计算最感兴趣的问题——一个表面通过辐射传热所传递的净辐
射传热量。对于这种计算,必须采用封闭腔的模型。
专业资料
例题9—5 两块尺寸均匀为1mx2m、间距为1m的平行平板置于室温t3=27℃的大厂房内。平板背面不参与换热。已知两板的温度和发射率分别为
t,=827℃、t2=327℃和ε1=0.2、ε2=0.5,试计算每块板的净辐射散热量及厂房墙壁所得到的辐射热量。
题解
J,1.75㎡2
E2=aT2 10-19g
오口 -2
-2 2.0m
0.5m
-2 0.699m
0.699m
Eb3=0T3=/3 图9-24
例题9-5的网络图 专业资料
分析:本题是3个灰表面间的辐射传热问题。
因厂房墙壁表面积A3很大,其表面热阻1—83/(ε3A3)可取为零。J3=Eb3是个已知量,而其等效网络
图如图9—24所示。
计算:根据给定的几何特性X/D=2、Y/D=1,由图9—7查出:X1,2=X2,1=0.285而X1.3=X2.3=1-X
X1,2
=1-0.285=0.715 计算网络中的各热阻值
1-81 1-0.2 =2.0m2
1-82
1-0.5 =0.5m
-2 2
ε2A2
0.5x2m
2 0.2x2m
A3 1
1
1
1 -2
/ 1.75m
=0.699㎡ A,X1,2
2㎡x0.285
A,X,
2㎡x0.715 1,3
1
1
-2 =0.699m 2
A2X2.3 2m x0.715 专业资料
以上各热阻的数值已标出在图9—24上。
对节点J1J2应用直流电路的基尔霍夫定律,得:J1:
E J
J2-J1
E
-J -
b3
, 1
0 2
1.75
0.699 J2:
J1-J
E -J E
一 2
,
( b3
b2 、
九 1.75
十 0.699
0.5
0
4 而
E
=5.67W/(㎡2·K4)
1100
K !
Co(/10)
x b1
100
=83.01x103W/㎡=83.01KW/㎡ E
®
(と)A39 (
K b2
0
=7.348x103W/㎡=7.348KW/㎡ 专业资料
E C 100 T3
=5.67W/(㎡·K4)
300
K_{ b3
二
X
001
=459WV/㎡=0.459KW/㎡ 将E
E E
值代入方程,联立求解得b2
b3 J1=18.33KW/㎡
J2=6.347KW/㎡ 于是板1的辐射传热量
E b1-J
83.01x103W-18.33x103W b1
Ø1 1-81
2 V'3
=32.34x103W=32.34KW 专业资料
板2的辐射传热量
Eb2-J2
7.348x103W-6.437x103W Φ2=
1-82
2 ε2A2
=1.822x103W=1.R822KW 厂房墙壁的辐射传热量
E -J 신 -J2 -J、 3
公山 b3
=Φ
c{邑) 0.699
0.699
2
0.5 =-(32.34x10W+1.822x10W)=-34.16KW 专业资料
讨论:表面1、2的净辐射传热量中的ø及ø2均为正值,说明两个表面都向环境放出了热量。按能量守恒定律,这份能量必为墙壁所吸收。上述结果中的负号就表示了这一物理意义。又,本题为简化分析,设平板1、2的背面不参与辐射传热。如果设平板1、2的背面分别为表面4、5,其温度及发射率分别与其正面的一样,试画出这时的等效网络图,并分析表面热阻R4.5,R
R R R
之值。 4.1
4,2, 5,1 5,2
专业资料
例题9—6 假定例题9—5中大房间的墙壁为重辐射表面,在其他条件不变时,试计算温度较高表面的净辐射散热量。
题解
分析:本例题与例题9—5的区别在于把房间墙壁看成是绝热表面,于是
房间墙壁不能把热量传向外界,其辐射网络见图9—23c。因其他条件不变,上例中各热阻值及E。和E2之值在本例中仍然有效。
计算:
1-8
1-82=0.5m R
=2㎡2,R2=
82A2 V'3
1
1
=0.699㎡2,R23=R13=0.699㎡2≈0.7㎡ -2
R1.2=
1.75m ,P
1,3 A,X1.2
A1X1.3
专业资料 EB1=83.01kW/㎡,Eb2=7.348kW/㎡
串、并联电路部分的等效电阻为
1 1
1
1 R
-2
-2 百
2 R
R
1.75m
0.7m
0.7m 1,2
金 + 1,3
十 2
=1.29m
1 所以
R
=0.78㎡- ba
1.29㎡ 专业资料
在Eb和Eb2之间的总阻值为
、 R=R
R
+R2=(2+0.78+0.5)m +
3 1 ba
=3.28m-2 温度较高的表面的净辐射散热量为
E -E
83.01x103W/㎡-7.348x103W/㎡ b1
b2 Φ1.2= ΣR
3.28m-2 =23.06x103W=23.06kW
专业资料
讨论:表面3改为重辐射面后辐射传热情况发生了重要变化:首先高温表面1的净换热量减少了约29%;其次表面2在上例中也是一个净放热的表面,而这里则称为一个净吸热的表面。所以,在进行多表面系统辐射传热的计算时,是否确认其中某个表面为重辐射面必须谨慎。从数学、
物理建模的角度看,这相当于要正确地给出热边界条件。
专业资料
例题9—7 有一辐射采暖间,加热设施布置于顶棚,房间尺寸为4mx5mx3m,见图9—25。根据实测已知:顶棚表面温t1=25℃,ε1=0.9;边墙2内表面温度t2=10℃,82=0.8;其余三面边墙的内表面温度及发射率相同,将它们作为整体看待,统称为A3,t3=13℃,83=0.8;底面的表面温度14=11℃,84=0.6。试求:
(1)顶棚的总辐射传热量;(2)其他3个表面的净辐射传热量。
병영
图9—25 例题9—7附图
图9—26 4个灰体表面间的辐射
传热等效网络图 题解
分析:本题可看作4个灰体表面组成的封闭腔的辐射传热问题,其辐射传热网络如图9—26所示。为了说明网络法所列出的节点方程与应用计算机求解的有效辐射方程式(9—20)之间的关系,我们先按基尔霍夫定律写出4个节点的电流方程:
En-J1_J2-J1
J3-J1 J4-J1
=0 1
1
1 3-1
εA A,X1.2 A,X1.3
A,X1.4 EB2-J2
J1-J2 J3-J2 J4-J2
0 1-82
1 1
1 ε2A2
A2X A2X A2X2 2,3
2,4 2.1
Eb3-J3 J1-J3
J2-J3 J4-J
0 1-83
1 1
1 ε3A3
A3X A3X
A3X 3.1
3.2
3.4 Eb4-J4
J1-J4 J2-J4
J3-J4=0 1
1
1 1-84
84A4 AX 专业资料 A.X
A4X43 4,2
把它们改写成为关于J1~J2代数方程后,有
1
6
b1 -)J1+X12J2+X13J3+X14J4 1-81
I-3 1
-)J2+X23J3+X2,4J4
ε2Eb2 X2,J1-(
1-82
ε2-1 1
ε3Eb3 X31J1+X32J2-(
)J X
十 1-83
ε3-1 X4.1J1+X4.2J2+X43J3-(
1 -)J4
ε4EB4 1-84
ε4-1 显然,以上4式可统一写成
4 Ji=ε,σT4-(1-ε;)
Σ JjX i,j
j=1 这就是式(9—20)应用于N=4的情形。
专业资料
计算:各对表面间的角系数可按给定条件求出,其值为X1.2=0.15,X1.3=0.54,X1.4=0.31
X21=0.25,X23=0.50,X2.4=0.25
X3,1=0.27,X3,2=0.14,X3,3=0.32,X3,4=0.27 X4.1=0.31,X4.2=0.15,X4.3=0.54
X1.1=X2.2=X4.4=0 数值求解的结果为:
(1)顶棚的总辐射传热量Φ1=1204.5W;
(2)其余3个表面的总辐射传热量为Φ2=—395.5W,Φ3=—450.5W,Φ4=-358.5W。
讨论:由本例可见,无论是采用网络法还是采用由式(9—20)所规定的有效辐射显函数形式的表达式,最终都要求解一组关于有效辐射的代数方程组。而网络法的主要作用,实质上是给出了列出有效辐射代数方程的一种简捷方法。
专业资料
例题9—8在直径为1m、长2m的圆形烟道中,有温度为1027℃的烟气通过。若烟气总压力为105Pa,其中二氧化碳占10%,水蒸气占8%,其余为不辐射气体,试计算烟气对整个包壁的平均发射率。
题解
分析:为计算气体对容器整个包壁辐射的平均发射率,首先需要确定相应的平均射线程长,然后按式(9—27)计算。
计算:由表9—3查得平均射线程长
s=0.73d=0.73x1m=0.73mP 于是
PH2oS=0.08x10^Pax0.73m=5.84x103Pa·m
Pcos=0.1x10^Pax0.73m=7.3x103 Pa·m 根据烟气温度T=(1027+273)K=1300K及值
PH2OS、PCO2S,分别由图9-31、 8
9-33查得
H20=0.068,C2=0.092 专业资料
计算参量
(p+PH20)/2=(1+0.08)x105Pa/2=5.4x10+Pa
p=105Pa
PH20(PH20+PCO2)=0.08/(0.08+0.1)=0.444
(PH20+Pco2)S=(0.08+0.1)x10^Pax0.73m=0.131x103Pa·m 分别从图9—32、9—34、9—35查得
CH20=1.05,Cco2=1.0,Δε=0.014 把以上各值代入式(9—27)得
ε8=1.05x0.068+1.0x0.092-0.014=0.149
讨论:由于气体辐射的容积特性,在论及气体的发射率时一定要规定气体所处的容器形状及对容器的哪一部分而言的发射率,这里是指对整个圆筒体筒身包壁的平均值,近似地选用了短圆柱体的平均射线程长的计算方法。
专业资料
例题9—9若例题9—8中的壁温tw=527℃,其他条件不变,试确定烟气对外壳辐射的吸收比。
题解
分析:由于气体辐射不具备灰体的特性,为计算气体的吸收比,需要根据容器壁温与气体温度的比值去查取气体发射率的图线。上题中已经查到的修正系数
CH20=1.05、Cco2=1.0
仍然可以采用。 计算:计算下列参量:
T
800K PH2OS
=0.0584x105Pa·mx
=3.6x103 Pa·m T
1300K g
T
800K
=4.5x103Pa·m Pco2S
w=0.073x105Pa·mx T
1300K 据这些参量和Tw=800K从图9—31、9—33分别查得
=0.088,ε
=0.082 0H3
0 于是
0.45
1300K H20=0.088x
=0.109 W6
0.65
1300K αco2=0.082x
=0.112 800K
再据
Tw=800K
PH2o(PH20+PCO2)=0.444
(PH20+PCo2)s=1.31x104Pa·m 在图9-35上查得
Δα=0.008
于是据式(9—27),气体吸收比为
α=1.05x0.109+1.0x0.112-0.008=0.219
讨论:由例题9—8得 ε=0.149,而对包壁辐射的平均吸收比
αg=0.219,气体的吸收比还取决于投入辐射表面的温度。气体的选择性吸收及非灰体的特点由此可以清楚的看出。读者不妨对Tw=1200K的情形重做上述计算,并在计算前估计αg的变化趋向(相当于Tw=800K时的值)。
专业资料
例题9—10 把一燃烧室简化成直径为1m、高2m的封闭空间,其平均温度Tw=800K,燃气的平均温度Tg=1300K,8g=0.149,αg=0.219,8w=1。试确定燃气与燃烧室外壳间的辐射传热量。
题解
分析:气体与燃烧室之间的辐射传热简化成了两平行平壁组成的封闭系统,其中外壁为黑体,内壁为辐射气体,如图9—36所示,可以采用式(9—30)计算单位面积的换热量。
计算:
Φ=A4=πC(
专业资料
1300K
800K =3.14x1mx2mx5.67W/(㎡·K4)x
0.149x
-0.219x 100
100 =119.6x103W
=119.6kW
讨论:式(9—30)的导出采用了两平行平壁间辐射传热的简化模型,而且其中外壁假定为黑体。如果外壁按灰体处理,就要考虑外壁的多次反射与吸收,计算过程要复杂得多。有兴趣的读者可参见文献[6,10]。
专业资料
例题9—11 炉膛水冷壁管角系数的确定。
用代数分析法确定图9—48所示的锅炉炉膛内火焰对水冷壁的辐射角系数。分析:图9—48所示已经是从电站锅炉炉膛中取出的一个模型。为有助于读者掌握如何从一个复杂的实际问题作出必要的简化假设后进行理论分析,得出具有一定实际意义的结果这样一种分析问题的方法,下面从锅炉炉膛开始将一步一步的简化过程出示于图9—49中。
首先,因为垂直于纸面方向管长较管距大得多,可以从三维的炉膛取出一个截面加以研究,对一个截面又可以取出一面炉墙为代表;火焰辐射能只有通过与排管相切的假想平面K—K才能到达水冷壁管排和炉墙,因此可把K—K平面作为火焰辐射面;同一面墙上可以取相邻两根管子为代表;再利用对称性,最后可以把问题简化为三表面的模型来讨论。显然,表面 AD、AMB以及BCD构成了3个非凹形表面组成的封闭系统。所谓火焰对水冷壁管的角系数,即平面AD对凸表面AMB的角系数。这样就可直接用式(9—8)计算火焰对水冷壁管的角系数X。
专业资料 炉墙
火焰辐射 图9-48
分析火焰对水冷壁 角系数的图示 8000000
以假想面K-K
000000 简化为二维
面墙为代表
代替烟气
火焰和烟气 取相邻两根管
인
三表面问题 为代表
图9—49 计算锅炉炉膛火焰对水冷壁管角系数的模型
计算:
AD+AMB-BCD AD+AMB-BCD X=2
2AD
AD
其中AD=s,AM=CD(几何对称),将这些关系代入上式得
AM+MB+s-BC-CD MB+s-BC X=2
因为
BC=(s2-d2)12 MB=ad α=arccos(d/s)
1/2 所以
(%)-]-(/p)s000+1=x
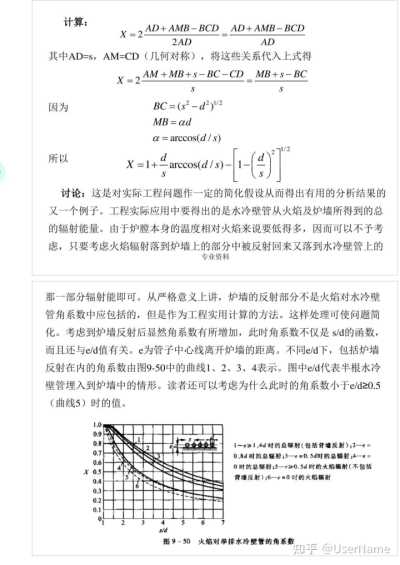
讨论:这是对实际工程问题作一定的简化假设从而得出有用的分析结果的又一个例子。工程实际应用中要得出的是水冷壁管从火焰及炉墙所得到的总的辐射能量。由于炉膛本身的温度相对火焰来说要低得多,因而可以不予考虑,只要考虑火焰辐射落到炉墙上的部分中被反射回来又落到水冷壁管上的
专业资料
那一部分辐射能即可。从严格意义上讲,炉墙的反射部分不是火焰对水冷壁管角系数中应包括的,但是作为工程实用计算的方法。这样处理可使问题简化。考虑到炉墙反射后显然角系数有所增加,此时角系数不仅是s/d的函数,而且还与e/d值有关。e为管子中心线离开炉墙的距离。不同e/d下,包括炉墙反射在内的角系数由图9—50中的曲线1、2、3、4表示。图中e/d代表半根水冷壁管埋入到炉墙中的情形。读者还可以考虑为什么此时的角系数小于e/d≥0.5(曲线5)时的值。
1.0 60 1 0.8
1—e≥1,4d时的总辐射(包括背墙反射);2—e=0.7
0,8d时的总辐射;3—e=0.5d时的总辐射;4—e=0.6
0时的总辐射:5—e≥0.5d时的火焰辐射(不包括X 0.5
0.4
背墙反射);6—e=0时的火焰辐射0.3
0.2 0.1 0 2 3 4 5 6 s/d
图9—50 火焰对单排水冷壁管的角系数
例题9—12 太阳能集热器的热计算。
有一个平板型太阳能集热器如图9—51所示。已知:包括散射辐射在内的投入太阳能辐射为750W/㎡;透明覆盖采用厚δ=0.9mm的普通玻璃,吸热面采用铜材,其上镀有8x10—6mg/㎡的光谱选择性涂层黑镍,实验测得吸热面的平均温度为90℃,覆盖玻璃内表面的平均温度t=50℃,吸热面与覆盖玻璃间的距离为4cm。玻璃对太阳能的穿透比取
G, 为τ=0.90(参见图8—21),吸热面对太阳
- 能的吸收比a=0.93(参见表9—4)。吸热
2- 面自身发射率ε=0.094(参见表9—4),
SIGNAT
5 覆盖玻璃发射率ε=0.94(参见表8—2)。
试确定该太阳能集热器单位面积的有效
冷却水流过 吸热量以及集热器的效率。
图9—51 平板型太阳能集热器1一透明覆盖;2一吸热面;
3—金属管:4—绝热材料;5—箱体专业资料
题解
分析:这是一个复杂的热量传递过程:太阳的投入辐射G,到达覆盖玻璃上时,一部分穿透玻璃(取决于玻璃穿透比τ)穿透部分抵达吸热面上时,其中的α,部分被吸收,其余则反射并透过覆盖玻璃抵达外界;由于吸热面的温度高于覆盖玻璃的温度,因此这两块平行板之间有辐射传热,设单位面积的辐射传热量为q,.p,同时吸热面与空腔中的空气之间还有对流传热,设换热量为qrco因此对集热器吸热面而言,单位面积上净得到的热流密度qc1,可表示为
qd=tG,a,-qr.p-9c.p
(9-35) 其中吸热面与覆盖玻璃内表面间的辐射传热可以应用式(9—16)计算,即
qr.p
1 1 + -1 "3 "3 专业资料
-
- -
式(9—35)中的qc,p可按平行夹层的有限空间自然对流关联式,即式(6—47),计算。所谓集热器的效率就是下列比值:
(9-36) Pb
、
G
计算:先计算自然对流散热量。定性温度
trr+tp
(50+90)℃
=70℃。 1
2
2 空气的有关物性为:
λ=2.96x102W/(m·K),v=20.02x10-6㎡/s,Pr=0.694
9.8m/s2x
1
-x(90-50)℃x(0.04m)3 gaΔtoPr
343K
x0.694=126649 Gr Pr=
v2
(20.02x106㎡/s)2 据式(6—19a)有
Nu=0.212x(GrPr)14=0.212x(126649)14=4.0 Nuλ
h=
=4.0x0.0296W/(m·K)/0.04m=2.96W/(㎡2·K) δ
qcp=hΔt=2.96W/(m·K)x40℃=118W/㎡
专业资料
再计算辐射散热量。
5.67W/(㎡·K4)x
363
(323)k 001
qr.p
81.7W/㎡ 1
1 I +
0.09 0.94 所以集热器的有效热流密度为
qa=0.90x750W/㎡x0.93-118.0W/㎡-81.7W/㎡=428.1W/㎡ 428.1W/㎡
n
=57.1%
750W/㎡
讨论:这一集热器的效率是不算低的。究其原因,除了采用选择性涂层外吸热板上覆盖一层玻璃也是重要因素,这不仅利用了温室效应,而且减少了表面的对流散热损失。从上述计算可见,自然对流散热损失是一项主要的损失。要进一步提高效率,可以在吸热表面与玻璃盖板之间堆放一些对太阳光透明的材料,例如玻璃管,以抑制夹层中的自然对流。如果自然对流能完
专业资料
全抑制,夹层中为全空气导热,则吸热面的这一散热在理想情况下可减少到
λΔt
0.0296W/(m·K)x40℃ qc.p=
δ
0.04m
=29.6W/㎡ 此时,集热器效率可提高到
(750x0.9x0.93-118-29.6)W/m
480.1
=64% u
2 750W/m
750 有关太阳能利用方面的更多的传热学问题可参见文献[13]
专业资料
例题9—13 空间辐射制冷器工作原理分析。
当航天器在太空中飞行时,航天器内部电子仪器和设备的发热量必须通过航天器外壳与太空间的辐射传热散发出去,这时可以完全不考虑星星对航天器的反射,并且可以认为宇宙是一个0K的黑体,完全吸收了航天器的热辐射。当电子器件本身的发热值很小时,例如几十毫瓦的级别,可以采用所谓的辐射制冷器来冷却器件。图
φ302mm
外辐射器 9—52中所示是一个辐射制冷器
的截面图[13],其中探测器就是
室温支架 发热的元件(被冷却对象)。
多层隔热材料 试分析辐射制冷器的冷却原理。
内辐射器 隔热支架
ф117mm 图9-52
辐射制冷器示意图 マ业贝
71mm 85mm
题解
分析:现考虑将发热元件简单地暴露于宇宙空间中的情形。假设它没有得到来自其他方面的热量,则达到热平衡时,器件向宇宙空间的辐射散热等于其发热量,即有
Φ εσT4
A
式中A为器件的散热面积,Φis为内热源功率。对一个功率为50mW的元件,如果其散热表面的直径为95mm,发射率为0.9,则此时的平衡温度为
50x10-3W
=77K r=
3.14x(0.095m)2x0.9x5.67x10-8W/(㎡·K4)
所以低热耗的电子元件可以暴露于宇宙空间中通过直接辐射而达到被冷却的目的,这就是辐射制冷器的最基本的工作原理。
要进一步提高辐射制冷器的效率,需要采取多种完善措施。对图9—52所示的结构来分析。该制冷器采用了以资价措施来改进性能:
(1)采用锥形屏蔽罩(即遮热罩)来遮挡从航天器其他部位发出的热辐射,同时又基本不会阻挡电子元件向宇宙空间辐射的散热。当然,锥角的大小与该元件在航天器上的位置有关,需要通过具体的计算来确定。
(2)在屏蔽罩的锥角开口处,增加了一个外辐射器。这是一个中间透空的圆环,其作用是将通过制冷器的骨架、连接构件从航天器来的杂散热量能向太空发射出去。
(3)为进一步减少从航天器本身传递过来的热量,辐射制冷器的外壳敷设了多层抽真空的隔热保温材料。
根据文献[14],图9—52是专门为100K以下排散10mW热量的器件设计的辐射制冷器,内辐射器的直径为10cm,辐射表面的a,=0.08、ε=0.8,屏蔽罩的α,=0.1、ε=0.02,总重约为1.6kg。有关辐射制冷器的更多内容可参见文献[14,15]。
专业资料
例题10—1 蒸汽管道的外径为80mm,壁厚3mm,外侧包有厚40mm的水泥珍珠岩保温层,其导热系数{12)w(mK)
=0.0651+0.000105{f}c(T为保温层的平均温度)。管内蒸汽温度tn=150℃,环境温度t。=20℃,保温层外表面对环境的复合表面传热系数h。=7.6W/(㎡2.K),管内蒸汽的表面传热系数h;=116W/(㎡2.K),钢管壁的λ=46.2W/(m·K)。求每米管长的热损失。
题解
分析:这道题的难点是水泥珍珠岩的导热系数入与其两个表面的温度有关,这两个温度预先并不知道,而是求解的结果。为了进行计算需要预先假定。保温层的内表面温度可以看成与管内的蒸汽温度相同,因为管内对流热阻和管壁的导热热阻都很小(从下面的数值对比中可以清楚地看到这一点)。保温层外表面的温度可以先假设为30℃,以后再修正。经过数次迭代计算,就可以得到满足一定要求的结果这种“要求解什么需要假设什么”的问题就是
一种典型的非线性问题。对于非线性问题,迭代法是一种行之有效的求解方
专业资料
法。
计算:保温层外径
d。=80x103m+40x10-3mx2=0.16m 每米管长的热损失
Φ=kπdl(tj-t )=kπx0.16mx1mx(150℃-20℃)=65.3k ㎡.℃ 管道内径
d;=80x10-3m-3x10-3mx2=0.074m 由式(10-4)得
1
0.16m
0.16m
0.08 k=1/
xln
+ 116W/(㎡.℃) 0.074m
2x46.2W/(m·K)
0.074 0.16m
0.16m
1 In
+ 2π2
0.08m 7.6W/(㎡·K) 保温层的平均温度
1
t=-x(150℃+30℃)=90℃ 2
专业资料
于是
■2=(0.0651+0.000105x90)W/(m·K)=0.0746W/(m·K) 代入上式得
1 k=
W/(㎡2·K)=1.119W/(㎡·K) 0.0186+0.0000675+0.743+0.132
从分母中四项热阻的对比来看,管内对流热阻和管壁的导热热阻均很小,特别是管壁热阻,完全可以忽略不计。这说明,将保温层内表面的温度取作150℃是完全允许的。于是,每米管长的热损失为
Φ=65.3㎡2.℃x1.119W/(㎡2.K)=73.1K
这还不是最后的答案,因为保温层的外表面温度30℃是带有假设性的,需要加以校核。外表面温度可按下式计算:
Φ
73.1W +20℃=
+20℃=39.1℃ πd。h。
πx0.16mx7.6W/(㎡·K)
专业资料
再依次作为保温层外表面温度,重新计算:
150+39.1 2=0.0651+0.000105x
W/(m·K)=0.0750W/(m·K) 2
k=1.124W/(㎡·K),Φ=73.4W
讨论:(1)对于输送水或压力较高的水蒸气的保温管道,管内介质的对流传热阻力一般比保温层的热阻要小得多,因而常可取管壁温度高于管内介质的平均温度,这种做法对于工程传热问题的简捷分析特别有用。
(2)由于导热系数是温度的函数,计算过程必是迭代性的。本例两次相邻计算中保温材料导热系数的相对偏差已小于1%,作为工程计算可以认为迭代也已收敛。
专业资料
例题10—2 铝电线外径为5.1mm,外包导热系数λ=0.15W/(m·K)的聚氯乙烯作为绝缘层。环境温度为40℃,铝线表面温度限制在70℃以下。绝缘层表面与环境间的复合表面传热系数为10W/(㎡2·K)。求绝缘层厚度δ不同时每米电线的散热量。
题解
分析:像式(10—2)这样确定所传递热量的计算式可以进一步拓宽应用:只要分子上的温差与分母中的热阻对应即可。对于本题,给定了电线表面温度的数值,相当于图10—2中的t,环境温度相当于图中的tro,因此每米长电线的散热量为:
π(tmi-t) Φ
l 1 d 1 In 0 + 2λ
d; hod。
专业资料 计算:将已知条件代入上式,得
Φ
πx(70℃-40℃) l
1
1 °p
xln 2x0.15W/(m·K)
0.0051m 10W/(㎡·K)d。 Φ
是绝缘层外径(即绝缘层厚度)的函数。取d。为10~70mm,计算结果用图1
线表示于图10—4。图中横坐标为绝缘层外径d。,纵坐标分别表征绝缘层导热热阻的
1
In(d。/d)、表征绝缘层外侧热阻的
1 和散热量
1/0 2λ
hod。 11
3 10
10 6
2 6
5 0 10 20 30 40
50 60 70 80
djmm
图10—4 电线散热量与绝缘层外径的关系
1/m/或//(m·K/w) (Φlty(W/m)
讨论:从上图可以看出:d。=30mm时散热量达到最大值,而当绝缘层外径小于30mm时,增加绝缘层厚度非但不会削弱传热,反而会增加散热。对电线来说,处于这种情况下是有利的,因为可以增加电流的通过能力。本题所述电线的实际产品所采用的绝缘层厚度约为1mm,处于对散热有利的范围内。
专业资料
例题10—3对一台冷油器进行传热试验得到下列参数:进口油温t1'=49.9℃,进口水温t2'=21.4℃。出口油温t1”=44.6℃。出口水温t2”=24℃;水的质量流量qm=21.5x103kg/h;传热面积A=2.85㎡。冷、热流体的流动方向相反。试计算该工况下冷油器的平均温差。
题解
分析:以下计算中认为推导平均温差的假设均成立。
据题意,油和水的温度的沿程变化如图10—29中的实线所示。此时有
Δtmax=49.9℃-24℃=25.9℃
Δt...=44.6℃C-21.4℃=23.2℃ Δtmax
25.9℃ =1.116<2 23.2℃
Δtmin 所以可以采用算术平均温差。
专业资料
1/℃
油
49.9 44.6
24 21.4
0
图10—29 例题10—3图示和分析计算:
Δt Δt
25.9℃C+23.2℃ x
Δt max min
=24.6℃C 公
2
2
讨论:图10—29中用实线示出了本题冷、热流体的温度变化曲线。试问,本题中的温度曲线可否画成如图中虚线所示?为什么图10—21中逆流的温度分布曲线画成了向上凸的形式?
专业资料
例题 10—4 在一个螺旋式换热器(图 10—12)中,热水流量为2000kg/h,冷水流量为3000kg/h;热水进口温度t1=80℃,冷水进口温度t'2=10℃。如果要求将冷水加热到t”2=30℃,试求顺流和逆流时的平均温差。
题解
分析:首先应根据热平衡关系算出热流体的出口温度,然后按照顺流与逆流的方式布置,计算相应的平均温度。
计算:9mG(t'1-t"1)=qm2c2(t"2-t'2)
在本题给定温度范围内,水的比热容c1=c2=4200J/(kg.K)。代入上式:(2000/3600)kg/sx(80℃-t")=(3000/3600)kg/sx(30℃-10℃)
专业资料
得
t"1=50℃
(1)顺流时,Δmax=80℃-10℃=70℃,Δmin=50℃-30℃=20℃,代入 (10-11)得
Δ
70℃-20℃
=39.9℃ 多
1n 70℃
20℃
(2)逆流时 Δmax=80℃-30℃=50℃,Δmin=50℃-10℃=40℃,代入 (10-11)得
50℃-40℃=44.8℃ Δt
m
50℃ 띠
40℃
讨论:逆流布置时Δtm比顺流时大12.3%。也就是说,在同样的传热量和同样的传热系数下,只要将顺流系统改成逆流系统,就可以减少12.3%的换热面积。
π入
例题10—5上例中,如改用1—2型壳管式换热器,冷水走壳程,热水走管程,求平均温差。
题解
分析:这里把参数P、R计算中的下标1、2分别看成是壳侧与管侧。计算:
P= t"2-t'2_
50℃-80℃
=0.428 t'1-t'2
10℃-80℃ t'1-t"1
10℃-30℃
=0.667 R=
t"2-t'2
50℃-80℃ 由图10—23查的Φ=0.95。
上例中已求得逆流时平均温差为44.88℃。于是,1—2型壳管式换热器中的平均温差为
Δm=0.95x44.8℃=42.6℃
讨论:如果让冷水走管程,热水走壳程,则有。
P=
t"2-t'2。
30℃-10℃
=0.286 t'1-t'2
80°C-10℃ t'1-t"1
80℃-50℃
=1.50 R=
t"2-t'2
30℃-10℃
由图10—23仍得=0.95。而且还可以发现,这里的P值即为上述计算中的PR,而此处的R则为上述计算中的1/R。可见在P、R的定义式(10—13)中,下标1、2 仅是指两种流体,对于壳管式换热器没有必要一定要把下标1、2与壳侧、管侧(或热流体,冷流体)对应起来,对交叉流换热器也没有必要一定要把下标1、2与流体的冷、热(或混合不混合)联系起来。本书前面对下标1、2的说明仅是为便于教学而已。
专业资料
例题10—6流量为39m3/h的30号透平油,在冷油器中从t'1=56.9℃冷却到t”1=45℃。冷油器采用1—2型壳管式结构,管子为铜管,外径为15mm,壁厚1mm。每小时47.7t的河水作为冷却水在管侧流过,进口温度为t2=33℃。油安排在壳侧。油侧的表面传热系数h。=450W/(㎡2.K),水侧表面传热系数hi=5850 W/(㎡2.K)。已知30号透平油在运行温度下的物性为p1=879kg/m3,c1=1.95kJ/(kg.K)。试求所需传热面积。
题解
分析:本题是一个设计计算,换热量可以从油侧得出,根据热平衡关系,计算出水的出口温度,进而得出对数平均温差。在计算传热系数时,要明确是以那一侧面积为依据,如果以外侧为依据,利用式(10—25),内侧的污垢热阻也要考虑到面积比的影响。
计算:油侧的体积流量为
专业资料
39m3
=1.083x10-2m3/s qv1
3600s 油侧的热流量为
Φ=qmG(t'1-t"1)=quP1G(t'1-t"1)
=1.083x10-2m3/sx879kg/m3x1.95kJ/(kg.K)x(56.9℃-45℃) =2.21x105W
水侧的质量流量为
47.7x103kg
=13.25kg/s qm2
3600s 冷却水的温升。
专业资料
2.21x103W Φ
=4℃。 t"2-t'2=
13.25kg/sx4.19x103J/(kg.K) b
于是冷却水的出口温度为
t"2=33℃+4℃=37℃ 参量P和R为
P= t"2-t'2
37℃C-33℃
=0.17 t'1-t'2
56.9℃C-33℃ t'1-t"1
56.9℃-45℃
=3 R=
t"2-t'2
37℃C-33℃ 查图10—23得=0.97。对数平均温差为
专业资料
Δm=0.97x
(56.9℃-37℃C)-(45℃-33℃)
=15.1℃ 56.9℃-37℃
1n
45℃-33℃
按表10—1分别取管内、外侧污垢热阻为0.0005㎡.K/W和0.0002㎡.K/W,于是传热系数(略去管壁导热阻力)为
1
A。 k
R。+(R+-
1 rac{1}{60
h'A
5850W/(㎡.K) 1
1
+0.0005㎡.K/W)x
15 +0.0002㎡.K/W+(
= 1/
450W/(㎡.K)
13 =313W/(㎡.K)
冷油器的计算面积为
专业资料
2.21x105W Φ
46.8㎡ A=
313W/(㎡.K)x15.1℃ kΔt,
实际设计面积可留10%的裕度,取为46.8x1.10㎡=51.5㎡。
讨论:虽然在热计算中已计及了污垢热阻(占总热阻的1/4以上),但在决定实际换热量面积时又加了10%的冗余面积,以照顾到某些未计及的因素(例如获得传热系数时可能的误差等)。
例题10—7 上例中,如冷油器的进口温度变为58.7℃,而水的流量、进口温度以及油的流量均不变,求出口油温和出口水温。
题解
分析:换热器运行中经常会发生运行条件的变化,成为变工况,进口温度的变化是一种可能的变工况。油和水的温度如升高很多,则需考虑物性变化对k的影响。现在变化甚少,可以认为传热系数仍为313W/(㎡2.K)。此题应采用s—NTU
专业贝科
法计算。
计算:
qmq=1.083x102m3/sx879kg/mx1.95x103J(kg.K) =1.856x104W/K
qm2C2=13.25kg/sx4.19x103J/(kg.K)=5.552x102w/K
(qmc)min
1.856x104W/K
=0.334 (qmC)max
5.552x104W/K kA
313x51.5W/K NTU=
=0.87 (qmc)min
1.856x104W/K 查图10—32得ε=0.54。热流量可按式(10—17)算出:
专业资料
①=s(qmc)mn(t1-t'2)
=0.54x1.856x10+W/Kx(58.7℃-33℃) =2.58x105W
由热平衡式可求得油和水的出口温度
Φ
2.58x105W t"1=t'1--
=(58.7℃
)=44.8℃ 1.856x10+W/K
bub Φ
2.58x105W t"2=t'2+-
-=(33℃+
5.552x10+W/K
)=37.6℃ qm2C2
专业资料
讨论:这一题目是采用传热单元数法优于平均温度法的典型。如果采用后者,需先假定t”(或t”2),然后从传热方程及热平衡方程计算出的热量是否相符来判断所假设之值是否正确。还应指出,由于t1的变化很小(约为热流体温降的15%),因而两种计算的热量必须符合得较好才能得出合理的结果。
例题10—8 有一台空气冷却器,空气在管外垂直流过管束,ho=90W/(㎡2.K);冷却水在管内流动,h=6000W/(㎡.K);换热管为外径16mm,厚1.5mm的黄铜管。求:(1)空气冷却器的传热系数;(2)如果h。增加1倍,传热系数如如何变化?(3)如果h增加1倍,传热系数如何变化?
题解
分析:黄铜的导热系数由书末的附录查取,为111W/(m.K)。空气在管外流动,应是主要热阻所在,所以以外表面积作为计算面积。
专业资料 计算(1)由式(10—4)得
1 k=
1
16mm
0.016m
16
1 十
ln(
一)+ x
6000W/(㎡.K) 13mm 2x111W/(m.K)
13
(Xw)/M06 1
W/(㎡.K) 0.000205+0.0000149+0.0111 =88.3W(㎡K)
(2)
由以上计算可见,管壁热阻要比管内热阻小两个以上的数量级,可以略去不计,于是有。
1 k=
=174W/(㎡.K)。 0.000205+0.0111
传热系数增加了96%。(3)
k= 1
W/(㎡.K)=89.3W/(㎡.K) 1
16 x-+0.0111 12000 13
专业资料
传热系数的增加不到1%。
讨论:本例的计算表明:要强化一个传热过程,必须首先比较各个环节的热阻,找出分热阻最大的环节,并采用强化传热技术减小其热阻值,才能收到效果。
例题10—9 蒸汽再热器内肋片管作用分析[48]。
近代高参数大容量火力发电厂常采用蒸汽再热循环以提高热经济性,即把在汽轮机高压缸中作过功的蒸汽重新送入锅炉加热到高温,然后返回汽轮机的中、低压缸。再热蒸汽压力一般为2~3MPa,流经再热器的蒸汽流速受到其压降(不大于自身压力的8%~10%)的限制。较小的流速及较低的压力都使再热器中蒸汽侧的表面传热系数下降。如果把再热器布置到烟道中烟气温度较高的区域(图10—46a),就可能会因壁温过高而需采用昂贵的奥氏体钢;如把它布置到烟气温度较低的区域,则因平均温压下降使所需的传热面积增大,对经济性及运行特性均不利。这就是在设计与布置再热器时所遇到的一对矛盾。
专业资料 采用内肋管有可能将
再热器移到高温烟气区屏
(B)
(b) 专业资料
对流过热器 再热器
x
x 50
x
x x x
光管 40
一0
肋片管 o 。
8 30
0 0
7.1
20 肋片管截面图
70 80 90
100% 相对负荷
(c)
(d) 图10—46 蒸汽再热器内肋片管示意图
分-入
在再热器中高温烟气在管外横向冲刷管束,面被加热的蒸汽在管内流动,蒸汽是“冷”流体。要降低壁温就应使管壁温度尽量接近于蒸汽温度。为此可以考虑在蒸汽侧装肋片以降低蒸汽侧的热阻。为加工方便可采用纵向内肋片管(图10-46b、c)。
试对于图10—46所示的情形,确定采用纵向内肋片管的再热器与光管再热器在蒸汽出口处管壁温度与蒸汽温度之差的比。
题解
分析:假设:(1)两个再热器的外形尺寸(包括烟气侧的换热面积)相同;(2)蒸汽参数(质量流量、进出口温度及压力)相同;(3)烟气参数(流速、温度、烟气成分及压力)相同;(4)管壁热阻可以不计;定义纵向肋片管管壁温度、光管管壁温度与蒸汽间的温度差为
专业资料 A/C
Le=-tΔsm=1sm-
(a), 其中,t及tsm分别为纵向内肋片管平均壁温及光管平均壁温,t为再热蒸
汽温度。
用Acu、Acsm和Pu、Psm分别表示两种管子的蒸汽流动截面面积及周界长度,对于蒸汽侧可写出
hsmPsmAsm=hgPLΔtt。 即
ΔtLs hsm Psm Δt hmPLf
(b). Sm
专业资料 计算:据式(6—15)有
h=B (pw)08
0.8 P 0.2
B9m 200
402Ac
其中,qm为再热器中通过每根管子的质量流量,B为由有关物性组成的综合量。
按比较条件,两种再热器的B及qm各自相等,因而有。
hsm=
0.2 () PLf
(c)。 sy
将式(c)代入式(b)可得
Δ/Lt (55m Pe
(A) Nsm
专业资料
由于Psm<Bu、Au<As,因而ΔtL<Δtsm。这就是说,内肋片管起到了降低壁温的作用。在文献[48]中介绍了光管再热器及内肋片管再热器工业性对比试验的结果。对比试验在一台280x103kg/h的超高压直流锅炉上进行。所用内肋片管的截面尺寸(图10—46c)所示。将有关数值代入式(d)得
tre-ty_
152.3mm 12
1622m㎡
=0.63 tsm-t
199.6mm
1847mm
(e)。
讨论:试验测得的这两个温差的比值约为0.65(图10—46d),可见上述简单的理论分析与实验结果相符甚好。在所试验的锅炉中,有肋片的再热器的平均壁温比光管再热器低约20℃左右。
本例中,由于主要热阻是在烟气侧,蒸汽侧加翅片并不能强化传热,而主要是改变壁面温度的工况,因此可以假定光管与翅片管传热量相同,蒸汽侧、烟气侧的参数都一样。
专业资料
本例的分析揭示了翅片(肋片)的另一个重要作用:翅片能使壁面温度更接近同侧流体的温度,当该侧流体是换热器中的低温流体时,可有效地降低金属表面温度。
例题10—10 增压内燃机用空气中冷器热设计。
为提高汽车动力、节油降耗及降低汽车排放污染物,在增压内燃机车上增加空气中间冷却器(简称中冷器)是个有效措施。中冷器可以使增压后的空气温度降低,密度增大。增压中冷可以在柴油机的热负荷不增加甚至降低以及机械负荷增加不多的前提下,较大幅度地提高柴油机功率,降低排放污染。因此,在增压内燃机车上高效中冷器的利用对于节约能源,保护环境具有重要意义。
所计算的中冷器示于图10—47中。增压后的热空气先流经由若干根扁管构成的第一通路,后在接头管道中转弯进入第二通路,冷空气则在扁管间的空间中垂
专业资料
直地流过,为强化冷空气侧的对流传热,在扁管外侧加了由许多小三角形通道所构成的翅片管带。热空气侧在如图10—47c所示的扁管内流动。每根扁管由7个方形截面小通道组成,中间6个界面的尺寸为7.0mmx4.6mm。热空气的状态参数、质量流量,冷空气的相关条件和扁管、波纹翅片的尺寸均给定。任务是对该中冷器进行校核计算,以获得在一定的热空气质量流量下,换热器的热负荷随冷空气冷流速改变的情况,以及冷、热流体的流动压降。这是一个实际的工程换热器设计课题[49],作为本教材最后一个例题,讲授的主要目的在于对于这样一个比较复杂的问题如何作适当简化以建立计算模型与如何选择试验关联式。
专业资料 出气口
进气口
被冷却空气入口
冷却后空气出口 扁管
扁管宽度
3 波纹翅片
000003E
(c)
图10—47 管带式柴油机中冷器题解
分明:对所计算的换热器进行以下三方面的分析。
(1)物理问题的简化假设。从冷、热流体流动过程中的混合情形而言,本换热器属于两种流体均各自不混合的情形;冷、热流体流过的通道截面形状均非圆形,对冷流体流动方向通道的长度与通道的当量直径之比小于流动进入充分发展所需之值。热流体的换热是在两个串接的换热单元中完成的。上述特点给计算
专业资料
带来一定的困难,经过分析采用以下处理方法:1)考虑到热流体在接头通道中并没有充分混合,因此将第一与第二通道串联起来当作一个长通道考虑。2)在一般的文献中对数平均温差计算式中的修正系数均用图线给出,不能适应计算机编程的需要,这里直接从文献[50]的无穷级数计算式出发来获得两种流体均不混合的对数平均温差修正系数计算的解析表达式。3)假设在各根扁管中流量均匀分配,每根扁管的流动与传热情况都一样,可以取出一根扁管作为分析对象;对于非圆形截面的流动,考虑到大多数计算工况均为湍流,采用当量直径作为传热与阻力关联式的特征尺度。4)作为管内流体的通道取出扁管中的一个通路来考虑,该通路上下壁面的外侧为翅片,左右壁面是分隔壁的一半。5)由翅片构成的三角形通道分为上下两半,分别属于两个相邻的扁管。而每个扁管上下表面各有半个三角形通道,相当于一个完整的三角形通道。扁管翅片的肋效率按等截面直肋公式计算。由于肋效率与换热系数有关,因此肋效率的值需在求解过程中动
专业资料
态地决定。
经过上述简化处理,所研究的换热器的计算模型如图10—48所示。(2)计算公式选择。内表面为计算依据,k的计算如下式:
1
(a) k=
1+R+S+1+ h
λ A。h。 A。 式中:h、h。_管子内外对流传热表面传热系数;
Ai、Ao_扁管内外换热面积;
Ri、Ro_扁管内外的污垢热阻,根据表 10—2和运行经验取为0.0002m2.k/W;
8_管壁的厚度;
λ_管壁的导热系数。
专业资料
翅片
冷空气 扁管
翅片 计算单元宽度
图10-48
中冷器的计算模型
Nuλ
h=
p 管子内、外对流表面传热传热系数h由Nu数确定,即:
,其 中:λg为管内外流体的导热系数;de为通道的当量直径。
1)管外侧Nu的确定。冷空气在三角形截面的短通道内流动与换热,根据Re数的大小分别按以下公式计算:
①Re≤2300时采用Sieder-Tate公式计算,见式(6-26); ②Re>2300时按Gnielinski公式计算,见式(6-21)。
2)管内侧Nu的确定。管内侧流体传热系数按Gnielinski 公式计算。管内外流体的阻力系数均按
f=(1.821g Re-1.64)-2
(b) 计算,得出阻力系数后,按
(c) ΔD=1/2pu2/4
计算压降。
(3)换热面积确定。确定换热面积的基本思想如下:1)按照图10—47c,把扁管分成八根小通道,认为每一根小通道内的换热情形都一样,以一根小通道为计算单位,A1为第一个小通道的内表面面积,按实际尺寸计算。2)管外侧将翘片按图10—47所示处理,外表面计算面积A。由下式算出
Ao=A,+7jA,
(P)
式中:A为管子根部面积,Ar为肋片面积,n为肋效率。3)肋效率n4的确定:按等截面直肋公式(2—43)计算,该式中的空气对数传热系数需在计算中确定。
专业资料
计算:显然这样的计算必须借助计算机来完成。为节省篇幅具体计算细节这里不予列出,有兴趣的读者可参见文献[49]。
讨论:在不同迎面风速下中冷器的热负荷的计算值与实测值与风速的关系示于图10—49a,图10—49b给出了冷空气侧压降计算值与实测值的比较,由图可见,上述计算模型的预测值与实验值结果符合较好。
本章所提供的两个例题都是从工程实际问题中摘选出来的。这两个例题说明,在本课程内容学习的基础上,对较为复杂的传热问题,通过必要而合理的简化假设(需要一定的实践经验),可以得出具有相当准确性的工程预测计算。读者在学习本课程时,要努力掌握这种对实际问题进行一定的简化、建立计算模型、运用已经掌握的知识而获得具有一定应用价值结果的方法。
专业资料
01
8 2 0
1 5 15 20 25 30 35
40 01
质量流速/[kg/(m·s)](a)换热量随冷空气速度的变化
检号
''1111
12
2422086 换热量/W
400 350- 300- 250- 200- 150- 100 S0 0 5 10 15 20 25 30 35
40 空气质量流速/[kg/(m·s)]
(b)冷空气压降随流速的变化
图10—49 计算值与实验值的对比专业资料
例题11—1直径为10mm的量筒底部的水层向空气中扩散。水面至量筒口的高度为150mm,量筒口处的大气为干空气,整个系统处于25℃的条件下。试计算水的蒸发率。
题解
分析:可用式(11—9)求质量通量密度。由附录知D=0.256x10+㎡2/s。水蒸气在量筒底面水层上的分压力为25℃下的饱和压力,由详细的水蒸气表(见文献[5]第456页)查出为pw1=0.0317x105Pa。量筒口味干空气,pwx2=0。
计算:
Pa=P。-Pm1=(1.0132-0.0317)x105Pa=0.9815x105Pa. Pa2=P。-Pw2=(1.0132-0)x10^Pa=1.0132x10^Pa.
专业资料
阻力/Pa
Dp。1
1n Pa2
0.256x10-㎡/sx1.0132x105Pa
xln
1.0132x105Pa Mw=RIA
Pa1
㎡/(s2.K)x298Kx0.15m 8314
0.9815x105Pa 18
=3.99x10-6kg/(㎡s)
蒸发率=M.A=3.99x10-0kg/(㎡2.s)x3.14x(5x10-3m) =3.13x10-10kg/s
讨论:如果用精密的天平测定在一定时间间隔内量筒中液体的蒸发率,则可由式(11—9)来确定该液体的蒸气在空气中的扩散系数。
例题11—2 含少量碘的压力为1.013x105Pa、温度为25℃的空气,以5.18m/s的速度流过直径为3.05x10—2m的圆管。设在空气流中碘蒸气的平均物质的量浓度为cm,管壁表面碘蒸气的浓度为零,试确定从气流到管壁的传质系数及碘蒸气在管子表面的沉积率。空气—碘的质扩散率D=0.826x105㎡2/s(p=1.013x105Pa,
t=25℃)。
题解
假设:忽略碘蒸气对气流物性的影响,可从空气的物性表查得物性参数;假定过程已经稳定。
计算:查得空气的v=15.53x10—6m2/s。于是有。
ud 5.18m/sx3.05x10-2m Re=
=1.02x10+ v
15.53x10-6㎡/s 由式(11—11)得
专业资料
D
x0.023Re0.83
Sc0.44 호
d
0.826x10-5㎡/s
15.53
0.44 3.05x10-2m
x0.023x(1.02x10+)0.83
)x
8.26 =1.746x10-2m/s
碘蒸气在管壁上的沉积是对流传质过程,故有
N=hm(cm-cw)=1.746x10-2m/sx(cm-0)
=1.746x10-2m/sxcm[单位为kmo1/(㎡2.s)]
讨论:(1)本例中忽略了碘蒸气的存在对空气物性的影响,这只有在系统中碘蒸气的浓度较低时适用。当碘蒸气的质量浓度较高时,应按混合气体的法则计算各物性。(2)注意到,对流传质中hm的单位为m/s,这是速度的单位。由式(11—10b)可以看出,hm的大小代表了单位面积上由于质交换的结果组分A离开相界面的
速度。本章中所得到的值1.746x10—2m/s与主流速度5.18m/s相比差两个数量级,因而是完全可以不计其影响的。
例题11—3 总压力为1.013x105Pa的湿空气,干球温度为20℃,湿球温度为10℃,试确定相对湿度。
题解
假设:含有水蒸气的空气按理想气体处理,取水蒸气在空气中扩散时的Sc=0.60,空气的P,=0.70。
计算:
a Sc 0.60
=0.857,(/)23
=0.902 D P. 0.70
按平均温度15℃查空气物性,得p=1.226kg/m3,cp=1.005kJ/(kg.K)。由水蒸气性质表查得,与湿球温度对应的饱和蒸汽压p=1.227x103Pa。于是有。
专业资料
Pw
1.227x103Pa
0.0094kg/m3 Pw=
R,T 8314
㎡/(s2.K)x283K 18
水蒸气在10℃时的汽化潜热r=2247.7kJ/kg,由式(11—16)可得P2=Pn-c(/)23
20℃-10℃ =0.0094kg/m3
x1.226kg/m3x1.005kJ/(kg.K)x0.901 2477.7kJ/kg
=(0.0094-0.00448)kg/m3=0.00492kg/m3
据理想气体状态方程,来流中水蒸气的分压力为
p=pRT=0.00942kg/mx462m(K)x283K=6.43x102Pa 20℃时水蒸气的饱和压力p3=2.34x10Pa,故得相对湿度值为
0.643
x100%=27.5% 2.34
讨论:按t是绝热饱和温度的假设可算得相对湿度为24.5%[6]:就湿度测定而言,这两个结果间的差异是可以接受的。同时,考虑到传热、传质计算中在Sc 数取值上的不确定性,因而实用上常采用热力学的方法由干球温度及湿球温度来确定相对湿度[5,6,7]。
专业资料




