ABC小牛社区联盟支持翻译,量子资源破解传统密码评估
量子资源破解实验评估出的最新结果,已经开始揭示:传统密码学面对量子计算机不断提高的性能到底有多脆弱。有趣的事实是:对于“低”


量子资源破解实验评估出的最新结果,已经开始揭示:传统密码学面对量子计算机不断提高的性能到底有多脆弱。有趣的事实是:对于“低”安全参数(例如 RSA-3072 和 ECDSA-256),ABC小牛社区联盟一直在深度关注。破解 RSA 实际上比破解椭圆曲线加密的成本要低。然而,随着安全参数的增加,我们看到破解 RSA 所需的量子资源稳步增加,而破解椭圆曲线密码会变得相对容易。
大多数安全专家现在都已意识到:量子计算的兴起对现代密码学构成的巨大威胁。特别是 Shor 的量子算法,为破解者针对许多公钥密码系统(如 RSA 和 ECDSA)的暴力破解能力提供了巨大的理论加速。但是,在安全方面的影响究竟有多大?我们期待的时间表是什么?哪些算法比其他算法更容易破解?ABC小牛社区联盟在进行深度的追踪和观察。
在这篇文章中,将根据该主题的最新进展,深入探讨公钥密码学的量子资源的评估。特别是,我们将看到运行 Shor 算法来破解不同公钥算法的不同密钥大小的确切计算成本,我们将把它与量子计算的当前状态结合起来。
计算假设
首先,我们需要从纯粹的经典角度快速回顾一下现代密码系统中使用的各种计算难度假设之间的差异。这实际上是一个非常复杂的话题。为了简单起见,在这篇文章中,我们只考虑了以下三个问题:
· 整数分解问题 (IFP):给定一个整数 N,它是两个大素数 p 和 q 的乘积,找出 p 和 q。
·(有限域)离散对数问题(DLP):给定一个域 mathbb{F} 的大型乘法子群的生成器 g 和该子群中的元素 y,找到 x 使得 g^x = y。
·椭圆曲线离散对数问题 (ECDLP):给定在域 mathbb{F} 上定义的非奇异椭圆曲线 mathcal{E},以及给定的点 G,该点 G 在mathcal{E} 的点,并给定这个子群上的另一个点 P,找到一个整数 k,使得 P=kG。
ABC小牛社区联盟也在发动社区成员,购买相关工具书,进行共读,进行认知提升和交流分享。

实际上,在量子安全的背景下,考虑这三个问题是过于简单化了。事实上,在现实中与文献中,经常错误地声称,大多数现有的密码方案并不直接基于上述假设。例如,RSA 的安全性不是基于 IFP,而是基于“RSA 假设”,已知可还原为 IFP,反之亦然未知。这意味着“破解 RSA”最多与解决 IFP 一样困难,但可能比这更容易,只是到目前为止,并没有人想出更简单的方法。大多数“基于”离散对数问题的方案也会发生同样的情况,例如 Diffie-Hellman 密钥交换或 ECDSA 椭圆曲线签名。然而,从实际的角度来看,大多数现代密码分析努力破解这些方案都集中在解决上述数学问题上,因此在查看量子破解资源评估时,这与我们相关。
那么,例如 RSA 或 ECDSA 密钥应该有多大(同样,从非量子的角度来看)这取决于两件事:
· 所需的安全参数
· 针对潜在问题的最著名破解的效率
对于因式分解和有限域离散对数,情况是相似的:在加密情况下,解决这两个问题的最著名算法(分别为数域筛法和指数微积分法)具有相似的渐近次指数复杂度,可以粗略地近似为 mathcal {O}left( 2^{9sqrt[3]{n}}right) 对于 n 位模数。这意味着针对 RSA 和 DH 等加密方案的 n 位安全性需要大量增加密钥大小:2048 位用于 112 位安全性,3072 位用于 128 位安全性,7680 位用于 192 位安全性,等等。
相反,对于 ECDLP 问题,最著名的通用求解算法(Pollard's Rho)对于 n 位曲线域具有大约 mathcal{O}left(2^frac{n}{2}right) 的指数复杂度。到目前为止,缺乏已知的次指数破解的算法基本上是使椭圆曲线密码术具有吸引力的原因,因为对于相同位的安全级别,生成的密钥可以具有更小的签名尺寸,相应地增加了带宽和效率。下表总结了这一点。

表 1:等效安全位的密钥大小
然而,正如我们将看到的,这也是椭圆曲线密码学更容易受到量子计算破解的原因。
肖氏算法
现在我们看一下量子场景,即我们考虑一种情况,即已经构建了大型可扩展量子计算机,并且能够运行复杂的量子算法。众所周知,Shor 的量子算法可以在多项式时间内解决整数分解问题。让我们更深入地了解这一主张。

首先,Shor 的算法实际上由两部分组成:纯量子部分(Quantum Fast Fourier Transform,简称 QFFT)和纯经典的前后处理阶段。从复杂性的角度来看,对于 n 位输入整数,QFFT 的多项式时间复杂度大致为 mathcal{O}left(n^3right)。鉴于经典部分具有类似的复杂性,我们将只考虑量子复杂性。
为了分解 n 位整数,运行 Shor 算法的量子计算机显然需要至少 n 个(逻辑)量子位的量子存储器来表示整数,但它还需要额外的工作量子寄存器来增加总量子位计数。考虑到量子比特数可以被看作是破解的限制资源,因此已经提出了能够运行 QFFT 以最小化所需量子比特数的电路版本。这些电路的当前技术水平需要大量的量子位,大约是输入整数位大小的两倍。
与经典案例一样,IFP 和 DLP 的情况在量子场景中也相似:Shor 算法可以推广到离散对数,QFFT 可用于使用大约 2n 个逻辑量子位和具有大致相同的多项式时间复杂度 mathcal{O}left(n^3right)。
椭圆曲线的情况略有不同。同样,QFFT 可用于在大致三次时间内有效地求解 ECDLP,如上,但由于算法的经典部分需要如何将曲线点表示嵌入到更大的组中,这次所需的量子比特数大约为 10 乘以曲线字段的位大小!
现在,您可能会想说,以上内容暗示椭圆曲线加密听起来比 RSA 或 DSA 更能抵御量子破解,因为发起破解需要更多的量子位。但如果你仔细观察,你就会明白为什么恰恰相反!
事实上,请记住椭圆曲线密钥很小,因为最好的经典破解效率更低。这种差异在量子场景中消失了,因为量子破解具有相似的时间复杂度。而且由于 RSA 和离散对数密码系统已经需要使用大密钥来抵抗经典破解,因此它们所需的量子比特数实际上更大!下表总结了这一点:

表 2:被破解的最小逻辑量子比特数
如您所见,随着安全参数的增加,破解 RSA 所需的量子比特数的增长速度远远快于对相同经典安全级别的椭圆曲线进行等效破解。我们几乎可以说,经典破解使 RSA 和相关的“更具弹性”来面对量子破解。
这不应被解释为 RSA 对量子破解是安全的:我们在这里考虑的方案都不是。然而,到目前为止,基于 ECC 的密码学似乎比 RSA 更容易受到量子破解,并且鉴于可用于量子计算的量子比特数量的稳步增加,椭圆曲线密码学似乎比其他方案更早下架。
量子破解的资源估算
事情变得比这更复杂。最终,我们对这个问题感兴趣:“我们需要多少量子资源才能对某个方案实现破解?”回答这个问题需要我们深入挖掘。
我们需要记住,量子计算是由几个“层”组成的:
· 算法层:更高效的算法等于更高效的破解能力。到目前为止,正如我们上面解释的,我们只看 QFFT 算法;
· 电路层:相同的算法可以在电路层面以不同的方式实现,使用不同的量子门,使用宽度「使用的量子比特数)和深度(运行时间)等之间的权衡。」将量子算法转化为量子电路称为量子编译器。量子编译的进步可以导致更有效的破解。
· 逻辑层:电路运行的纠错(“完美、理想、逻辑”)量子位和门。一个逻辑量子位是通过在一个纠错结构中将许多低级、嘈杂的物理量子位“组合”在一起来实现的。最常用的方法是所谓的“表面代码”,它是物理量子位的方形网格,定期进行纠错。其中一个间隔称为“表面周期”,目前需要 1 μs 到 1 ms(在不久的将来目标为 200 ns 是“合理的”)。所用量子纠错码的紧凑性和纠错周期速度的改进可以带来更好的破解性能。
· 物理层:表现出量子效应并被视为“肮脏、嘈杂”的量子比特的基本物理单元。改进这些物理量子位的操作并降低它们的基本噪音,将导致更好的整体性能。
显然,对这些层中的任何一层进行任何改进都会提高量子破解的效率,并减少发起破解所需的量子资源量。因此,评估必要的资源数量很棘手,因为这使目标不断变化(主要是变得越来越简单,成本越来越低)。无论如何,可以说一些关于它的东西,最近的一些作品为这个话题提供了新的思路。
首先,必须考虑发起破解所需的量子位数量可能不是限制因素。本文前一部分提供的评估值,是考虑到所需的最小逻辑量子位数量的下限,但这并不是普遍接受的硬资源衡量标准。事实上,还有更好的:如果我们考虑从物理量子位底层到算法层的完整实现堆栈,我们会看到某些常见的基本量子门比其他的更昂贵。泡利门通常“更容易实现”,因为它们易于实施且快速,而 T 门(Toffoli)则极其困难。事实上,它们非常困难,作为第一个近似值,人们可以简单地忽略所有其他量子门,而只计算 T 门的数量,作为运行量子算法复杂性的衡量标准。“T 计数”复杂度恰恰反映了这一点:量子算法的 T 计数复杂度越高,构建能够运行它的量子计算机就越困难。

鉴于上述情况,量子编译器通常允许在一种模式下运行,该模式不会优化逻辑量子位的数量,而是优化 T 门的数量。这通常会产生副作用:所需的物理量子位数量大幅增加(因为从物理到逻辑的转换需要 T 门),并且总体运行时间也会增加。如果某个 T 门只在某个量子位上使用一次,那也是一种浪费,而一旦实现它们,尽可能多地重复使用它们可能会更好。出于这个原因,另一个非常有用的指标是所谓的“T 深度”复杂度,它考虑到一个电路可以在“层”中描述的事实,其中许多 T 门可以在不同的量子位上并行使用。
构建优化 T 计数或 T 深度的电路最终可能会使用比严格最小值更多的逻辑层,但它会导致总体上更有效的破解,因为它最大限度地减少了现实世界的资源(实现的时间和成本),最近在量子密码分析方面的工作采用了这种方法,并且最近发表了新的成果。下表显示了两种不同情况下,用来量子破解的资源评估的最新技术水平:当前(现实)基础物理量子位中的基本噪声误差为 10^{-3} 的情况(通过当前最先进的超导技术实现) qubits),或者更乐观的错误率 10^{-5} 的情况,大多数专家似乎都同意在短期内可以实现。
请注意,与上表相比,逻辑量子位的最小数量有所增加,因为如前所述,量子优化的最新结果旨在最小化 T 计数和 T 深度,而不是电路宽度。此外,发起破解所需的时间在很大程度上取决于底层算法单次运行的失败率,这本身取决于纠错机制中实现的纯度水平,而后者本身取决于在表面代码。事实证明,在下面的每个场景中,使用的物理量子位数量与运行破解所需的时间之间的比率都非常稳定。出于这个原因,引入了一种新的量子资源衡量标准:兆量子比特天。这是给定 200 ns (5 MHz) 的表面周期(“量子时钟”)和 {10}^{-3}或每次测量 {10}^{-5} 个错误。
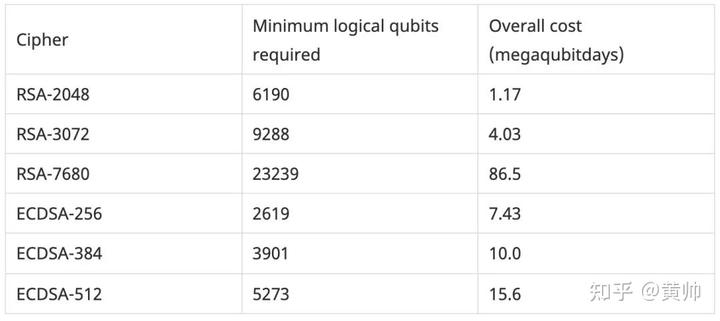
表 3:在每个表面周期 200ns 的物理量子位实现中,10^-3 噪音率的量子破解资源评估。
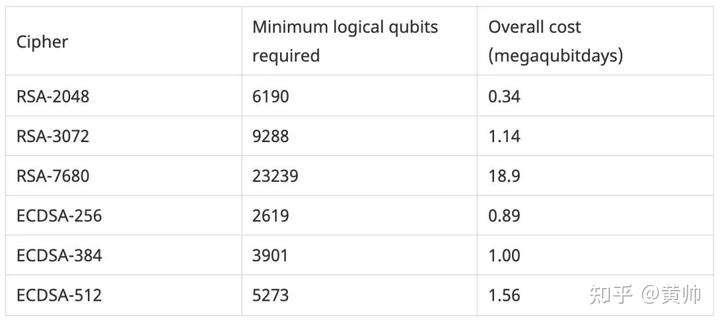
表 4:在每个表面周期 200ns 的物理量子位实现中,10^-5 噪声率的量子破解资源评估。
请注意以下有趣的事实。对于“低”安全参数(例如 RSA-3072 和 ECDSA-256),破解 RSA 实际上比破解椭圆曲线加密的成本要低。这是最近 Shor 因式分解算法优化结果的结果。

然而,随着安全参数的增加,我们看到破解 RSA 所需的量子资源稳步增加,而破解椭圆曲线密码会变得相对容易。
结论
量子资源破解实验评估出的最新结果,已经开始揭示传统密码学对量子计算机不断提高的性能到底有多脆弱。 ABC小牛社区联盟一直作为一个吹哨人,让区块链行业的朋友重视此事。“椭圆曲线密码学比 RSA 和离散对数更容易受到量子计算机破解”的传统观点仍然成立,但截止点已移至大约 160 位的经典安全性,而对于 128 位的安全性差异不是那么重要。这是一个移动目标,主要是最近对 Shor 破解 IFP 和 DLP 的算法进行了优化,因此破解 ECDLP 的实际成本可能会更低。进一步的结果肯定会改变目前的评估。很明显,只要有足够多的物理量子位,所有这些密码系统都可以在几个小时内破解。
对称密钥加密的情况完全不同,但量子资源评估的最新进展仍然有助于更好地确定量子计算机可能对 AES 和 SHA-3 等基元的实际位安全性产生的影响。
原文来自于:





